Variations of Gravity
The Variations of Gravity are the supposed variations to gravity caused by the earth, moon and sun. Some precision devices are alleged to detect these variations, while other precision devices are unable to do so.
The Gravimeter
On analysis of the gravimeter we find that the device is not directly measuring gravitational acceleration at all. It is measuring noise and using many software algorithms to cancel out the noise. Every part of the device's components—the lasers which measure the motion, the springs which launch the mass up and down the small tube, and all component parts—are all connected in some manner to the earth, and are subject to noise and vibrations.
https://link.springer.com/chapter/10.1007/978-3-662-03482-8_9
“ One of the most serious problems for absolute gravimeters is the vibration disturbances. ”
Marine Gravimeters
Below we see an example of gravimetry devices and methods for marine gravimetric surveying:
http://www.iitk.ac.in/nicee/wcee/article/WCEE2012_1237.pdf
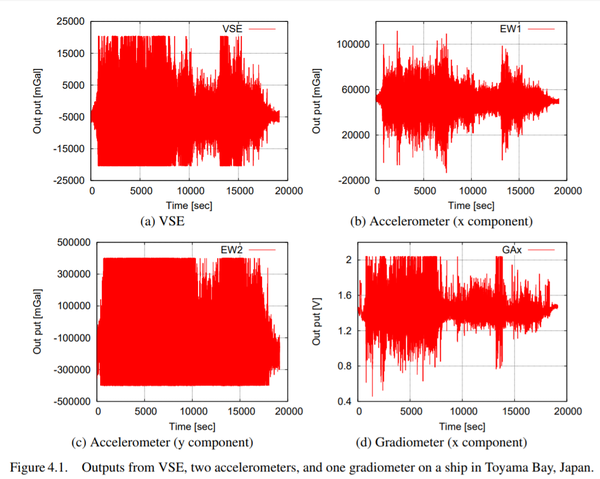
An example is given of outputs from VSE, Accelerometer, and Gradiometer devices on a mid-size ship navigating Toyama Bay, Japan:
“ FINDING GRAVITY FROM VERY NOISY DATA
In the previous section, the low-pass filter is used to find the gravity from the noisy data. We can expect that the variation of gravity consists of components with long period, however the vibration of carrier with short period. If this expectation is satisfied, the low-pass filter should work well. Actually, analysis for the first observation on an observation wheel works well, though, not for the other two observations. The reason is the difference of the amplitude of the noise: it is very difficult to pick up the gravity data with very small amplitude from very large vibration of the carrier. This must be limitation of simple filtering technique.
To reduce the vibration of the carrier, we can choose two different approaches. ”
From the above we see that a need to use algorithms and filters to 'find gravity' from noise. The levels of g are not readily apparent, and must be constructed by subtracting the noise to 'find gravity'. The above passage states that "We can expect to find the variations of gravity consists of components with long period, however the vibration of the carrier with short periods."
The reader may decide whether the process of subtracting vibrations with one characteristic to reveal other vibrations truly measuring gravity. Why does "gravity" need to be found?
Galathea-3: A global marine gravity profile
The Danish vessel Galathea-3 describes its methods for gravimetric surveying:
Galathea-3: A Global Marine Gravity Profile
“ The Galathea-3 navigation data included raw depth records provided by The Danish Hydrological Office. The data transfer was sometimes unstable and the data themselves were often very noisy. A preparation of such data for the Bouguer gravity processing requires a cumbersome data cleaning the removal of the spikes, the smoothing, and often the interpolation ”
We see that the process involves extensive data analysis, filtering, and cleanup from noise — to 'find gravity'.
Airborne Gravimetry
Airbourne gravimetery methods echoes the same:
Improving the Accuracy and Resolution of SINS/DGPS Airborne Gravimetry
“ Because the resulting signal is very noisy (see Sections 2.3.2 to 2.3.4 for details), its derivation is followed by a filtering step that removes most of the noise by low-pass filtering the data. ”
Again, we see that filtering is necessary to clean up the noise.
Land Based Gravimetry
The following paper describes the process of turning a laser signal into a "variation of gravity":
Ultra-high Precision, Absolute, Earth Gravity Measurements
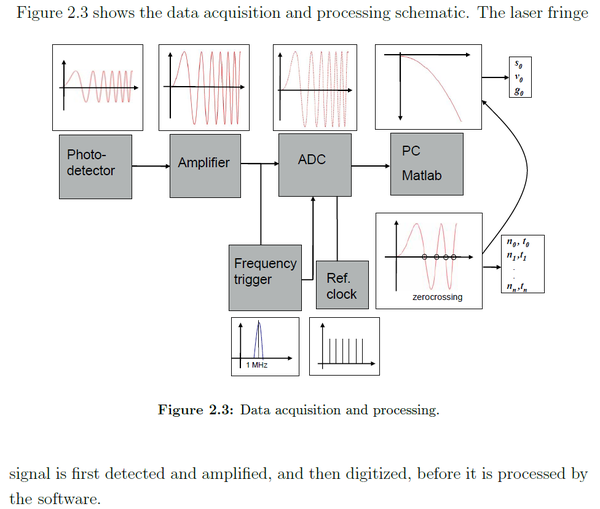
The paper describes that the fringe signal from the laser beam is digitized and processed:
“ One of the new features of our setup is that the whole fringe signal (with up to 1.6 million data points) is digitized and processed. In other gravimeters usually just parts of the fringe signal are used for data processing. Since the duration of our FB’s fall in the MPG-1 is about 200 ms, the resultant signal reaches a frequency of up to 6.2 MHz. As an industry standard, a sampling rate of at least 7 times the measured frequency is suggested. ”
Processing Steps
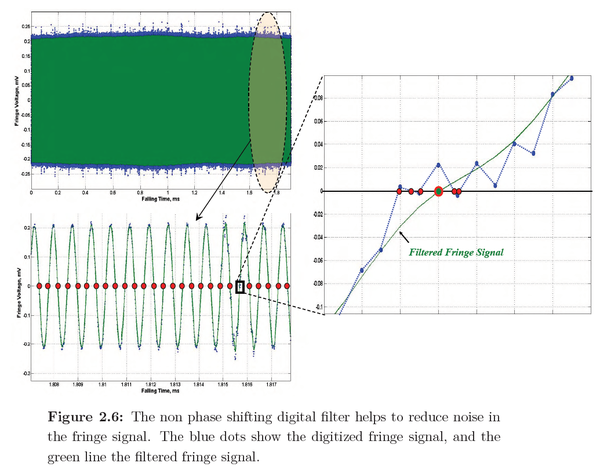
The fringe signal from the laser must be filtered with software:
The remainder of the document describes how the filtering occurs. All sources, to the best of the author's ability, is given an "uncertainty budget," to which is subtracted from the noise. The uncertainty budgets are estimated ranges to which a phenomenon may be contributing to the noise. All possible phenomena in nature must be considered and precisely defined. Everything from air drag, electrostatic fields, pressure, seismic vibrations, &c.
In the Table of Contents we find a list of tables, showing the various elements which are subtracted:
4.6 Uncertainty budget of the measured imbalance – Method II. . . . 84
4.7 Uncertainty budget: COM and OC adjusted – Method II. . . . . . 84
5.1 Uncertainty budget for air drag . . . . . . . . . . . . . . . . . . . 89
5.2 Uncertainty budget for outgassing . . . . . . . . . . . . . . . . . . 90
5.3 Uncertainty budget for eddy currents . . . . . . . . . . . . . . . . 91
5.4 Uncertainty budget for electrostatic field . . . . . . . . . . . . . . 91
5.5 Uncertainty budget for instrumental masses . . . . . . . . . . . . 94
5.6 Uncertainty budget for laser verticality . . . . . . . . . . . . . . . 96
5.7 Length standard specifications. . . . . . . . . . . . . . . . . . . . 96
5.8 Uncertainty budget for laser stability . . . . . . . . . . . . . . . . 97
5.9 Frequency standard specifications. . . . . . . . . . . . . . . . . . . 98
5.10 Uncertainty budget for clock stability . . . . . . . . . . . . . . . . 98
5.11 Uncertainty budget for corner cube rotation . . . . . . . . . . . . 98
5.12 Uncertainty budget for radiation pressure . . . . . . . . . . . . . . 99
5.13 Uncertainty budget for beam divergence . . . . . . . . . . . . . . 100
5.14 Uncertainty budget for temperature gradient . . . . . . . . . . . . 101
5.15 Uncertainty budget for seismic noise . . . . . . . . . . . . . . . . 107
5.16 Uncertainty budget for speed of light . . . . . . . . . . . . . . . . 108
5.17 Uncertainty budget for effective height . . . . . . . . . . . . . . . 109
5.18 Specifications of Photoreceiver. . . . . . . . . . . . . . . . . . . . 110
5.19 Uncertainty budget for amplifier . . . . . . . . . . . . . . . . . . . 111
5.20 Uncertainty budget for solid Earth tides . . . . . . . . . . . . . . 113
5.21 Uncertainty budget for ocean loading . . . . . . . . . . . . . . . . 113
5.22 Uncertainty budget for polar motion . . . . . . . . . . . . . . . . 114
5.23 Uncertainty budget for environmental pressure . . . . . . . . . . . 115
5.24 Uncertainty budget for Coriolis force . . . . . . . . . . . . . . . . 116
5.25 Uncertainty budget for MPG-1. . . . . . . . . . . . . . . . . . . . 117
5.26 Uncertainty budget for MPG-2. . . . . . . . . . . . . . . . . . . . 118
Once all of these items and their theoretical uncertainties are subtracted, we are left with "gravity."
In truth, the method is merely subtracting vibrations and then applying trend analysis.
Gravimeter Tides
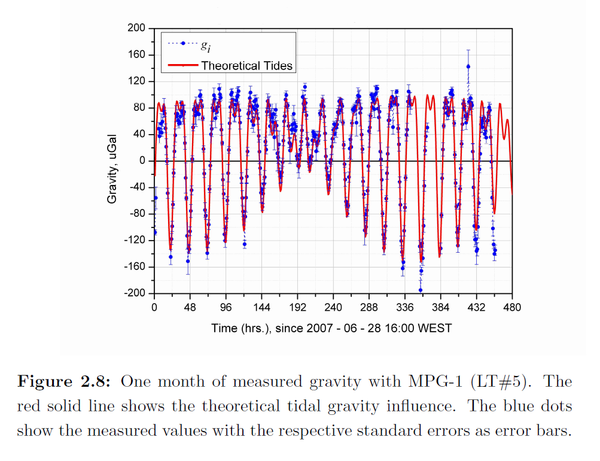
The above pdf mentions that long-term analysis of the gravimeter noise can detect the tides:
The main conclusion from this is that the tides may be related in some manner to vibration or noise that is being processed. No mechanism is presented, or is identifiable, from a long term analysis of vertical vibration trends.
Location Trends
Q. How is it that the level of g is different at high altitudes and at the poles?
A. The gravimeter measures fringe noise, not the "level of g". The output is the result of specialized filtering. That, after the final filtering and analysis, there may be trends at the top of a mountain, or in an environment which sits on a large amount of compressed ice, or with different environmental affects, should not be surprising.
The Torsion Balance
While the gravimeter relies on noise and vibration analysis, the types of experiments used in the equivalence principle tests are of a different sort. The equivalence principle tests are incredibly reliable precision machines which are used to measure the equivalence principal to increasing precision.
Experimenters have redesigned the torsion balance tests to try and detect the gravity variations caused by the sun, moon, and the tidal forces. It was found that the gravitational influence of the sun, moon, or the tidal forces could not be measured as being a function of the attraction of the bodies in the experiments. Variations to "gravity" did not appear.
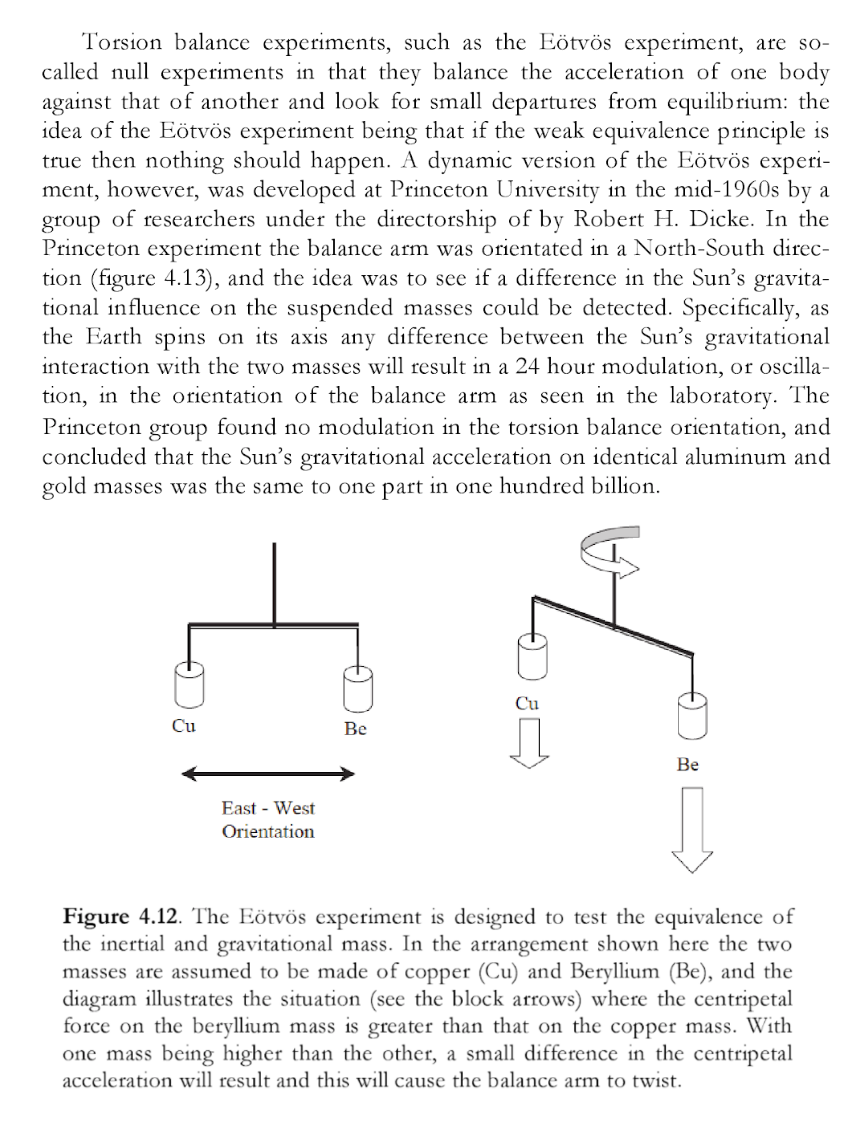
The Princeton Experiment
From 'The Pendulum Paradigm: Variations on a Theme and the Measure of Heaven and Earth', by Martin Beech, we read the following:
Essentially, the experiment is summarized as follows:
“ In the Princeton experiment the balance arm was oriented in a North-South direction (figure 4.13), and the idea was to see if a difference in the Sun's gravitational influence on the suspended masses could be detected. Specifically, as the Earth spins on its axis and difference between the Sun's gravitational interaction with the two masses will result in a 24 hour modulation or oscillation, in the orientation of the balance arm as seen in the laboratory. The Princeton group found no modulation of the torsion balance, and concluded that the Sun's gravitational acceleration on identical aluminum and gold masses was the same to one part in one hundred billion. ”
The masses were not attracted to the sun in the experiment, to an accuracy of one part in one hundred billion.
Repetitions
Additional experiments of this class are described. The first experiment in this list is the Princeton experiment above:
| Authors | Year | Description | Accuracy |
|---|---|---|---|
| Roll, Krotkov and Dicke | 1964 | Torsion balance experiment, dropping aluminum and gold test masses | difference is less than one part in one hundred billion |
| Branginsky and Panov | 1971 | Torsion balance, aluminum and platinum test masses, measuring acceleration towards the sun | difference is less than 1 part in a trillion (most accurate to date) |
| Eöt-Wash | 1987– | Torsion balance, measuring acceleration of different masses towards the earth, sun and galactic center, using several different kinds of masses | difference is less than a few parts in a trillion |
The Eöt-Wash experiments, which measured the acceleration of different masses towards the earth, sun, and galactic center was repeated by others:
https://plato.stanford.edu/entries/physics-experiment/app4.html
“ The torsion-balance experiments of Eöt-Wash were repeated by others including (Cowsik et al. 1988; Fitch, Isaila and Palmer 1988; Adelberger 1989; Bennett 1989; Newman, Graham and Nelson 1989; Stubbs et al. 1989; Cowsik et al. 1990; Nelson, Graham and Newman 1990). These repetitions, in different locations and using different substances, gave consistently negative results. ”