Astronomical Prediction Based on Patterns
This page will demonstrate that prediction in astronomy is based solely on patterns in the sky. Celestial events come in patterns and trends. By analyzing the patterns of past behaviors from historic tables it is possible to create an equation that will predict a future event. This is how prediction in astronomy has been performed for thousands of years, and how it is still performed today.
Ancient Astronomy
Ancient Babylonians
Astronomy for Physical Science - Cal State Long Beach (Archive)
“ The Babylonians accumulated records of astronomical observations for many centuries. The records enabled them to see repeated patterns in the motions of the celestial objects. They used the patterns to predict the positions of the Moon and planets. ”
From Mathematical Thought from Ancient to Modern Times: Volume One by Professor Morris Kline (bio) we see:
“ Babylonians calculated the first and second differences of successive data, observed the consistency of the first or second differences, and extrapolated or interpolated data. Their procedure was equivalent to using the fact that the data can be fit by polynomial functions and enabled them to predict the daily positions of the planets. They knew the periods of the planets with some accuracy, and also used eclipses as a basis for calculation. There was, however, no geometrical scheme of planetary or lunar motion in Babylonian astronomy. ”
Ancient Greeks
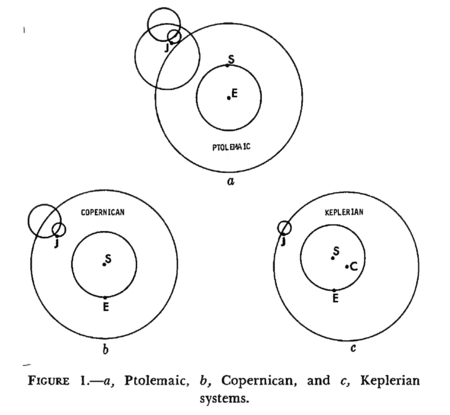
The Ancient Greeks believed in an stationary round earth-centered system, around which the Sun, Moon and planets revolved. Prediction in Ancient Greek astronomy was dominated by the epicycle; a small circle whose center moves around the circumference of a larger one. Originally devised by Hipparchus of Rhodes and later extended by Ptolmy of Alexandria, the purpose of the epicycle and related mechanisms were to account for differences from the ideal state.
In Chapter 2 of The Logical Leap: Induction in Physics by David Harriman (bio) we read:
“ The circle is the geometric figure possessing perfect symmetry, so Ptolemy and earlier Greek astronomers began with the intuition that celestial bodies orbit in circles at uniform speed. Observations then determined the deviations from the ideal, which Ptolemy modeled using mathematical contrivances unrelated to physical principles (deferents, epicycles, and equants).
...Ptolemy’s science was superficially anti-Platonic in that he emphasized the role of careful observation. However, at a deeper level, his science was a logical application of Platonism; in astronomy and in optics, he started with the “perfect” model and then merely described without explanation the inherently unintelligible deviations from it. ”
Modern Astronomy
Perturbations
In order to predict the path of planets modern astronomers calculate perturbations.
Description and Function
Gravitation Vs. Relativity (1922)
Charles Lane Poor, Ph.D. (bio)
Professor Emeritus of Celestial Mechanics,
Columbia University
“ The deviations from the “ideal” in the elements of a planet’s orbit are called “perturbations” or “variations”.... In calculating the perturbations, the mathematician is forced to adopt the old device of Hipparchus, the discredited and discarded epicycle. It is true that the name, epicycle, is no longer used, and that one may hunt in vain through astronomical text-books for the slightest hint of the present day use of this device, which in the popular mind is connected with absurd and fantastic theories. The physicist and the mathematician now speak of harmonic motion, of Fourier’s series, of the development of a function into a series of sines and cosines. The name has been changed, but the essentials of the device remain. And the essential, the fundamental point of the device, under whatever name it may be concealed, is the representation of an irregular motion as the combination of a number of simple, uniform circular motions. ”
Professor Poor gives an example of epicycles being used to predict patterns of phemomena:
“ The Tide Predicting Machine of the Coast and Geodetic Survey at Washington is a note-worthy example of the application of the mechanical method [of prediction via epicycles]. The rise and fall of the tide at any port is a periodic phenomenon, and it may, therefore, be analyzed, or separated into a number of simple harmonic, or circular components. Each component tide will be simple, will have a definite period and a constant amplitude; and each such component may be represented mechanically by the arm of a crank, the length of which represents the amplitude; each crank arm being, in fact, the radius of one of the circles in our diagram.
Such a machine was invented by Sir William Thomson and was put in operation many years ago. The machine at present in use at Washington was designed by William Ferrell. It provides for nineteen components and directly gives the times and heights of high and low waters. In order to predict the tides for a given place and year, it is necessary to adjust the lengths of the crank arms, so that each shall be the same proportion of the known height of the corresponding partial tide, and to adjust the periods of their revolutions proportionally to the actual periods. Each arm must also be set at the proper angle to represent the phase of the component at the beginning of the year. When all these adjustments have been made, the machine is started and it takes only a few hours to run off the tides for a year, or for several years. This machine probably represents the highest possible development of the graphical or mechanical method. It is a concrete, definite mechanical adaptation of the epicyclic theory of Hipparchus.
But, because the Coast Survey represents and predicts the movements of tidal waters by a complicated mass of revolving cranks and moving chains, does anyone imagine for a moment that the actual waters are made up of such a system of cranks? No more did Hipparchus believe that the bodies of the solar system were actually attached to the radial arms of his epicycles; his was a mere mathematical, or graphical device for representing irregular, complicated motions.
While the graphical, or mechanical method is limited to a few terms, the trigonometrical, or analytical method is unlimited. It is possible to pile epicycle upon epicycle, the number being limited only by the patience of the mathematician and computer. ”
Replacing the Foundations of Astronomy
In a 2017 paper Replacing the Foundations of Astronomy (Archive) its author Dr. Gopi Krishna Vijaya (bio) gives us a historic overview of the foundations of Astronomy. He describes that perturbations are epicycles, and that they are used in astronomy to 'make the observations fit' the theory:
Epicycles Once More
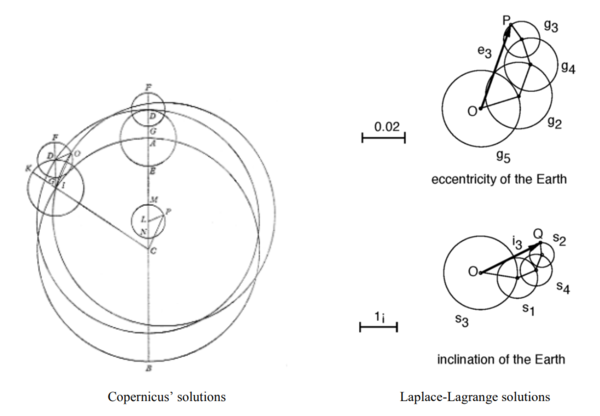
“ Following the Newtonian era, in the 18th century there were a series of mathematicians – Bernoulli, Clairaut, Euler, D’Alembert, Lagrange, Laplace, Leverrier – who basically picked up where Newton left off and ran with it. There were no descendants to the wholistic viewpoints of Tycho and Kepler, but only those who made several improvements of a mathematical nature to Newtonian theory. Calculus became a powerful tool in calculating the effects of gravitation of all the planets upon each other, due to their assumed masses. The motion of the nearest neighbor – the Moon – was a surprisingly hard nut to crack even for Newton, and several new mathematical techniques had to be invented just to tackle that.
In the process, a new form of theory became popular: Perturbation theory. In this approach, a small approximate deviation from Newton's law is assumed, based on empirical data, and then a rigorous calculation of differential equation is used to nail down the actual value of the deviation. It does not take much to recognize that this was simply the approach taken before Kepler by Copernicus and others for over a thousand years – adding epicycles to make the observations fit. It is the same concept, but now dressed up in gravitational disguise: ”
| Copernican Theory | Newtonian Theory |
|---|---|
| Circular motion is primary | Inverse square law is primary |
| Variations: epicycles | Variations: perturbations |
| 30 - 50 circle variables | 100’s of perturbation variables |
| Geometric techniques | Calculus techniques |
| Variables fit to observation | Variables fit to observation |
“ In other words, the entire thought process took several steps backwards, to redo the same process as the Ptolemaic - Copernican epicycle theory, only with different variables. The more logical way of approach would have been to redirect the focus of the improved mathematical techniques to the assumptions in Newton’s theory, but instead the same equations were re-derived with calculus, without examining the assumptions. Hence any modern day textbook gives the same derivation for circular and elliptical motion that Newton first derived in his Principia. The equivalence of the epicycle theory and gravitational theory has not been realized, and any new discovery that fits in with the mathematical framework of Newtonian gravity is lauded as a “triumph of the theory of gravitation.” In reality, it is simply the triumph of fitting curves to the data or minor linear extrapolations – something that had already been done at least since 2nd century AD. Yet the situation is conceptually identical.
~
The Dead End
In the late 19th century, one of the French mathematicians – Henri Poincaré – had already discovered that many of the terms being used in the “perturbation” series by mathematicians like Laplace and Lagrange were becoming infinite for long periods of time, making the system unstable. In simple words, the solutions ‘blow up’ fairly quickly. He also showed that the general problem of 3 mutually gravitating bodies was insoluble through any mathematical analysis! Many physicists and mathematicians built up modern “Chaos theory” based on these ideas, to show simply that one cannot calculate the movements of the planets accurately. Thus began the field of non-linear dynamics.
In the middle of the 20th century, with computers entering the field, the mathematicians pretty much gave up on calculating the orbits by themselves and programmed the computer to do it, even though it was mathematically shown that these orbits were incalculable. They had to be satisfied with approximations or numerical methods (or “brute force” methods.) The result of it all was that after 300 years, Newtonian/Einsteinian thought lands in the same spot that Kepler ended: the orbits point to a living or chaotic system. Only now, there is the additional baggage of all the wrong concepts introduced with regard to “inverse-square law”, “gravitational attraction”, “gravitational mass” and “curved space-time” along with uncountable number of minor assumptions. In this process, an enormous amount of human effort was put to derive thousands of terms in equations over centuries. The entire enterprise has been a wild goose chase ”
Underlying Model
Instead of than Ptolmy's perfect circle, perturbation theory in celestial mechanics uses a two body problem as the underlying model. From The Ever-Changing Sky: A Guide to the Celestial Sphere (Archive):
“ The deviations from a true two-body orbit are called the perturbations of the orbit. The concept of orbital elements is still used, but now they must be allowed to change. We define the elements at any given moment to be those that the orbit would have were the outside gravitational forces suddenly to vanish (sometimes called the oscillating orbit). A short time later, however, these forces have produced deviations from this calculated elliptical path, and we must then compute a new set of elements. We treat perturbations by defining the elements at a certain epoch and by establishing their rates of change with time. ”
General Application
Perturbation methods are, in fact, prevalent in many areas of science. From Perturbations in Complex Molecular Systems (Archive) we read the following:
“ In general perturbation methods starts with a known exact solution of a problem and add “small” variation terms in order to approach to a solution for a related problem without known exact solution. Perturbation theory has been widely used in almost all areas of science. Bohr's quantum model, Heisenberg's matrix mechanics, Feynman diagrams, and Poincare's chaos model or “butterfly effect” in complex systems are examples of perturbation theories. ”
The Wikipedia article on Perturbation Theory (Archive) echoes the same:
“ This general procedure is a widely used mathematical tool in advanced sciences and engineering: start with a simplified problem and gradually add corrections that make the formula that the corrected problem becomes a closer and closer match to the original formula. ”
The book Approximate Analytical Methods for Solving Ordinary Differential Equations states on p.65 (Archive):
“ The perturbation theory had its roots in early studies of celestial mechanics, for which the theory of epicycles was used to make small corrections to the prediction of the path of planets. Later, Charles Eugene used it to study the solar system, in particular the earth-sun-moon system. Now, it finds applications in many fields, such as fluid dynamics, quantum mechanics, quantum chemistry, quantum field theory, and so on.
The idea behind the perturbation method is that we start with a simplified form of the original problem (which may be extremely difficult to handle) and then gradually add corrections or perturbations, so that the solution matches that of the original problem. The simplified form is obtained by letting the perturbation parameter take the zero value. ”
Special Perturbations
From the Wikipedia section on Special Perturbations in celestial mechanics (Archive):
“ In methods of special perturbations, numerical datasets, representing values for the positions, velocities and accelerative forces on the bodies of interest, are made the basis of numerical integration of the differential equations of motion.[6] In effect, the positions and velocities are perturbed directly, and no attempt is made to calculate the curves of the orbits or the orbital elements.[2] Special perturbations can be applied to any problem in celestial mechanics, as it is not limited to cases where the perturbing forces are small.[4] Once applied only to comets and minor planets, special perturbation methods are now the basis of the most accurate machine-generated planetary ephemerides of the great astronomical almanacs.[2][7] ”
History
The Wikipedia article on Perturbation Theory provides a history:
“ Perturbation theory was first devised to solve otherwise intractable problems [Links us to the Three Body Problem Wikipedia page] in the calculation of the motions of planets in the solar system.
...Since astronomic data came to be known with much greater accuracy, it became necessary to consider how the motion of a planet around the Sun is affected by other planets. This was the origin of the three-body problem; thus, in studying the system Moon–Earth–Sun the mass ratio between the Moon and the Earth was chosen as the small parameter. Lagrange and Laplace were the first to advance the view that the constants which describe the motion of a planet around the Sun are "perturbed", as it were, by the motion of other planets and vary as a function of time; hence the name "perturbation theory". ”
Moon Model - Ancient to Present
The following paper by physicist Martin C. Gutzwiller (bio) describes a history of the model of the Moon. See the illustration on page 600 and its caption, and note that the lunar model was "adopted ever since."
Moon-Earth-Sun: The oldest three-body problem (Archive)
Martin C. Gutzwiller
“ V. THE MANY MOTIONS OF THE MOON
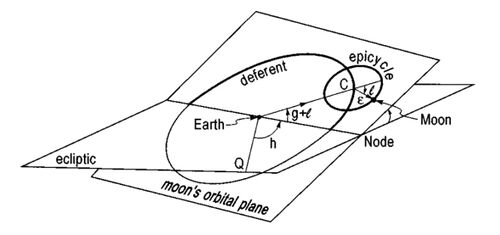
A. The traditional model of the Moon
A plane through the center of the Earth is determined at an inclination γ of about 5 degrees with respect to the ecliptic. The Moon moves around the Earth in that plane on an ellipse with fixed semi-major axis a and eccentricity ε of about 1/18. The Greek model was quite similar, except that the ellipse was replaced by an eccentric circle.
The plane itself rotates once every 18 years in the backward direction, i.e., against the prevailing motion in the solar system, while keeping its inclination constant. The perigee of the Moon, its point of closest approach to the Earth, makes a complete turn in the forward direction in about nine years.
The following picture (see Fig. 1) emerges: first we fix the direction of the spring equinox or some fixed star near it as the universal reference Q in the ecliptic: counting always from west to east, we determine the angle h from Q to the ascending node, i.e., the line of intersection for the Moon’s orbit with the ecliptic where the Moon enters the upper side of the ecliptic; from there we move by an angle g in the Moon’s orbital plane until we meet the perigee of the Moon; and finally we get to the Moon by moving through the true anomaly f. All these three angles have a double time dependence: linear (increasing for f and g, while decreasing for h) plus various periodic terms that average to 0.
- FIG. 1. The basic lunar model from antiquity (adopted ever since) consists of an orbital plane for the Moon containing an epicycle for its orbit; the crucial parameters α, ε, γ and the three angles l,g,h have their modern interpretation.
~
D. The evection—Greek science versus Babylonian astrology
The Babylonians knew that the full moons could be as much as 10 hours early or 10 hours late; this is due to the eccentricity of the Moon’s orbit. But the Greeks wanted to know whether the Moon displays the same kind of speedups and delays in the half moons, either waxing or waning. The answer is found with the help of a simple instrument that measures the angle between the Moon and the Sun as seen from the Earth. The half moons can be as much as 15 hours early or late. With the Moon moving at an average speed of slightly more than 30' per hour (its own apparent diameter!), it may be as much as 5° ahead or behind in the new/full moons; but in the half moons, it may be as much as 7°30' ahead or behind its average motion. This new feature is known as evection.
Ptolemy found a mechanical analog for this peculiar complication, called the crank model. It describes the angular coupling between Sun and Moon correctly, but it has the absurd consequence of causing the distance of the Moon from the Earth to vary by almost a factor of 2. In the thirteenth century Hulagu Khan, a grandson of Genghis Khan, asked his vizier, the Persian all-round genius Nasir ed-din al Tusi, to build a magnificent observatory in Meragha, Persia, and write up what was known in astronomy at that time. Ptolemy’s explanation of the evection was revised in the process. In the fourteenth century Levi ben Gerson of Avignon in southern France seems to have been the first astronomer to measure the apparent diameter of the Moon (see Goldstein, 1972, 1997). Shortly thereafter Ibn al-Shatir of Damascus in Syria proposed a model for the Moon’s motion that coincides with the theory of Copernicus two centuries later. The crank model was replaced by two additional epicycles, yielding a more elaborate Fourier expansion in our modern terminology (see Swerdlow and Neugebauer, 1984).
With the improvements of the Persian, Jewish, and Arab astronomers, as well as Copernicus, the changes in the Moon’s apparent diameter are still too large with +/- 10%. As in Kepler’s second law, the Fourier expansion (12) has to include epicycles both in the backward and in the forward direction, in the ratio 3:1. ”
The Foundations of Astrodynamics
In a paper titled The Foundations of Astrodynamics its aurthor Dr. Samuel Herrick (bio) says the same as all of the above, explaining that epicycles are still used.
“ Physical celestial mechanics may be said to have begun with Galileo Galilei, Isaac Newton, and the laws of force and gravitation. Astrodynamics and mathematical celestial mechanics, on the other hand, date back at least to Heracleides of Pontus in the fourth century B.C. The Greek invention of epicycles and eccentrics was developed into a system by Apollonius of Perga in the third century and Hipparchus of Alexandria in the second century B.C. It was refined and published by Ptolemy of Alexandria in the second century A.D., and came to be known as the Ptolemaic system. It is generally assumed that the epicycle was discredited by Johannes Kepler some 1500 years later, but in point of fact epicycles have persisted in astrodynamics down to the present day, and have extended their domain into other areas of science under the guise of Fourier series! ”
“ In modern perturbation theory we actually take account of the original epicyclic concept by combining several Fourier series that have arguments based upon different angular variables. ”
Kepler's Epicycles
The above paper describes that there were still epicycles in Kepler's version with elliptical orbit, and that they were never eliminated. Kepler just reduced it a little more. We can see that Jupiter is on an epicycle in Kepler's version:
Dr. Herrick explains that Kepler's epicycles were adopted into Newtonian mechanics (as Newtonian pertubations), and that progress then reversed, favoring the Copernican system of circles and epicycles.
“ When Newton‘s development of the law of gravitation made it possible to explain these perturbed deviations by mechanical means, the epicycles that had survived Kepler’s onslaught were adopted into Newtonian mechanics. As a matter of fact, the basic epicyclic theory re-expanded to include even the elliptic deviations, thus rejecting the Keplerian system in favor of the Copernican system, whose handling of the elliptic terms by systems of epicycles (rechristened “Fourier series”) proves to be simpler than the use of expressions in terms of Keplerian ellipses. In a sense this development may be noted as realistic astrodynamic replacement for a theoretical mathematical formulation. ”
Newton's Epicycles
After Kepler came Newton. Historian of Science William Whewell (bio) informs us that Newton used epicycles for the Moon:
History of the Inductive Sciences (1846)
“ 3.— The Epicyclical Hypothesis was found capable of accommodating itself to such new discoveries. These new inequalities could be represented by new combinations of eccentrics and epicycles: all the realand imaginary discoveries by astronomers, up to Copernicus, were actually embodied in these hypotheses; Copernicus, as we have said, did not reject such hypotheses; the lunar inequalities which Tycho etected might have boen similarly exhibited; and even Newton36 represents the motion of the moon’s apogee by means of an epicycle. As a mode of expressing the law of the irregularity, and of calculating its results in particular cases, the epicyclical theory was capable of continuing to render great service to astronomy, however extensive the progress of the science might be. It was, in fact, as we have already said, the modern process of representing the motion by means of a series of circular functions. ”
See Also: A Reintroduction of Epicycles - Newton's 1702 Lunar Theory and Halley's Saros Correction
University of Toronto Quarterly
At the end of the 19th century, long after Copernicus, Kepler and Newton made their contributions to astronomy, we read about the state of astronomy in a 1895 edition of University of Toronto Quarterly (Archive):
“ Of the modern employment of the Ptolemaic epicycles, De Morgan, secretary of the Royal Astronomical Society of London, wrote in 1844: “ The common notion is that the theory of epicycles was a cumbrous and useless apparatus, thrown away by the moderns and originating in the Ptolemaic or rather Platonic notion that all celestial motions must either be circular and uniform motions or compounded of them. But, on the contrary, it was an elegant and most efficient mathematical instrument which enabled Hipparchus and Ptolemy to represent and predict much better than their predecessors had done; and it was probably at least as good a theory as their instruments and capabilities of observation required or deserved. And many readers will be surprised to hear that the modern astronomer to this day resolves the same motions into epicyclic ones. When the latter expresses a result by series of sines and cosines (especially when the angle is a mean motion or a multiple of it) he uses epicycles; and for one which Ptolemy scribbled on the, heavens, to use Milton’s phrase, he scribbles twenty. The difference is that the ancient believed in the necessity of these instruments, the modern only in their convenience; the former used those which do not sufficiently represent actual phenomena, the latter knows how to choose better; the former taking the instruments to be the actual contrivances of nature was obliged to make one set explain everything, the latter will adapt one set to latitude, another to longitude, another to distance. Difference enough no doubt, but not the sort of difference which the common notion supposes.”
Such was the state of affairs fifty years ago; today epicycles may be said to possess the heavens above and the earth beneath and the waters and the air between, nor has the all-pervading ether escaped them. In analytic guise they dominate the mathematics of hydrokinetics and sound, of heat, light and electricity; in fact, wherever there is either periodic or irregular motion, there the mathematician “ scribbles ” his epicycles, and not content like Ptolemy to wheel them on simple circles he rolls epicycle on epicycle to the third, the fourth or the fifth degree. Nor does their influence end here. Machines have been made to record for a sufficient length of time any motions for the character of which a working theory has to be found; other machines analyse the records into epicyclic movements, smoothing out or rejecting accidental irregularities, and still other machines recombine the epicycles to predict the motions as they will occur at a future time or under given changes of condition. Thus we have mechanical tide-predictors, harmonic analyzers of meteorological phenomena, epicyclic tracers of deviation curves for the compasses in iron ships, and a fast increasing array of other such machines. ”
Evolution of the Solar System
A work by Dr. Hannes Alfvén (bio) titled Evolution of the Solar System (1976) shows that epicycles are still in use in celestial mechanics, more than 365 years after Kepler's discovery of elliptical orbits and 289 years after Newton's publishing of his Principia. Dr. Alfvén uses a combination of Kepler and epicycles:
https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19770006016.pdf (Archive)
https://history.nasa.gov/SP-345/contents.htm
The Motion of Planets and Satellites
3.1 The guiding-center approximation of celestial mechanics
3.2 Circular orbits
3.3 Oscillations modifying the circular orbit
p.40
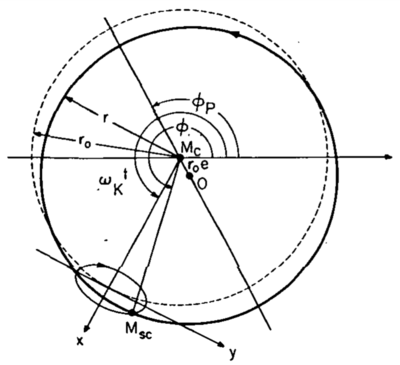
"FIGURE 3.3.1.—The guiding-center method of approximating the Kepler motion. The guiding center moves with constant velocity along the dashed circle of radius r0 in the center of which the gravitating mass Mc is situated. The body M moves in an “epicycle” around the guiding center. The epicycle is an ellipse with the axis ratio 2/1 and semiminor axis of er0. The epicycle motion is retrograde. The resulting motion of M is an ellipse which almost coincides with the undashed circle which has its center at O. The distance from O to Mc is er0. The position of the pericenter is given by Φp. The difference between the undashed circle and the exact Kepler ellipse is really less than the thickness of the line."
Perturbation Search
A search for 'perturbation' on nasa.gov shows that perturbations are used widely for many applications, including heavy use in celestial mechanics.
https://www.google.com/search?&q=perturbation+site:nasa.gov
No. of Results: 50,600
Jet Propulsion Laboratory Development Ephemeris
The Jet Propulsion Laboratory Development Ephemeris (JPL DE or DE) is a 'mathematical model of the Solar System' produced by the Jet Propulsion laboratory in Pasadena, California. It has been claimed that JPL DE is a simulation of the Solar System which is based on gravity. However, it is seen that it uses perturbation-based methods.
https://en.wikipedia.org/wiki/Jet_Propulsion_Laboratory_Development_Ephemeris
“ Each ephemeris was produced by numerical integration of the equations of motion, starting from a set of initial conditions. Due to the precision of modern observational data, the analytical method of general perturbations could no longer be applied to a high enough accuracy to adequately reproduce the observations. The method of special perturbations was applied, using numerical integration ”
NASA Horizons
NASA's Horizons On-Line Ephemeris System system makes similar statements in its methodology, suggesting that it is based on perturbation theory:
https://ssd.jpl.nasa.gov/?horizons_doc
“ Comet and asteroid ephemerides are integrated from initial conditions called "osculating elements". These describe the 3-dimensional position and velocity of the body at a specific time. The integrator starts with this state and takes small time steps, summing the perturbing forces at each step before taking another step. A variable order, variable step-size integrator is used to control error growth. In this way, the gravitational attraction of other major solar system bodies on the target body trajectory is taken into account. ”
Laskar, Lapace, Le Verrier
Great figures of science, such as Jacques Laskar, Pierre-Simon Laplace, and U. Le Verrier, used perturbation methods to predict movement in the solar system.
From p.157 of The KAM Story by Professor H. Scott Dumass we read:
“ Laskar at the Bureau des Longitudes (BdL) in Paris took a somewhat different approach to simulating the solar system over long times. Lacking access to a dedicated machine like the Digital Orrery, Laskar resurrected the methods of his early predecessors at the BdL by applying Laplace’s and U. Le Verrier’s perturbation methods to the equations of motion for the solar system. These methods begin by ‘averaging’ the effect of one orbit upon another (effectively smearing a planet over its orbit until it be- comes a ring), but they go much further: Laskar computed perturbation expansions (by machine) with as many as 150,000 terms in some cases. ”
VSOP
VSOP (French: Variations Séculaires des Orbites Planétaires) is a popular software package used to generate planetary ephemeris, which are the positions of the planetary objects in the sky. It is used in astronomy software such as Stellarium and Celestia. It has been alleged that VSOP uses a geometric RET model to make its predictions, and so VSOP and the astronomy software which uses it is therefore a validation of the theory. On assessment we find, however, that VSOP is based on the ancient epicyclic methods.
Comparing VSOP to the Ptolemaic System
The following is left by an editor on VSOP's Wikipedia Talk Page (Archive):
“ Modelling VSOP on a ubiquitous PC computer program, starting with only one element for each of the three parameters (L, B R) and then slowly incrementing the number of elements, gives a sense of irony that it is in fact nothing more than a more complex development of the ancient deferent / epicycle system used by Ptolemy. A system that despite being totally dismissed out of hand for being intellectually "wrong", was able to provide a prediction service accurate enough to match the observational resolution available (naked eye, with no reliable mechanical timekeeping). A system that, astoundingly to this author, was able to detect and measure, accurately, the lunar evection, one of the still-used perturbations of the Earth-Moon system. Summing powers of sines and cosines is certainly tantamount to circles upon (or perhaps within) circles; recursing, or perhaps simply nesting, almost endlessly. Whilst of course this is totally irrelevant to the mathematics, it perhaps behoves Wikipedia's wider terms of reference to include this as a philosophical point. ”
VSOP Perturbations
On p.331 of Planetary theories in rectangular and spherical variables - VSOP 87 solutions we read that VSOP is based on perturbation theory:
http://articles.adsabs.harvard.edu//full/1988A%26A...202..309B/0000311.000.html (Archive)
“ VSOP 87 contains the newtonian perturbations of the eight planets between themselves, the perturbations of the Moon on the Earth-Mood barycenter and on all the planets and the relativistic perturbations expressed in isotropic coordinates. ”
Comments from Celestia Developers
Celestia Developers comment on the large number of planet-specific terms used in computing positions:
https://celestia.space/forum/viewtopic.php?f=2&t=8285 (Archive)
“ VSOP87 is a set of polynomials describing the orbits of the major planets. There are over 1000 terms in each series. ”
https://celestia.space/forum/viewtopic.php?f=3&t=2592 (Archive)
“ I could add more terms to the VSOP-87 series, but there are already over 1000 per major planet ”
Fourier Analysis
In Encyclopedia Britannica's Celestial Mechanics article (Archive) by physics professor and astrophysicist Stanton J. Peale (bio) it says:
“ Nicolaus Copernicus assumed that Earth was just another planet that orbited the Sun along with the other planets. He showed that this heliocentric (centred on the Sun) model was consistent with all observations and that it was far simpler than Ptolemy’s scheme. His belief that planetary motion had to be a combination of uniform circular motions forced him to include a series of epicycles to match the motions in the noncircular orbits. The epicycles were like terms in the Fourier series that are used to represent planetary motions today. (A Fourier series is an infinite sum of periodic terms that oscillate between positive and negative values in a smooth way, where the frequency of oscillation changes from term to term. They represent better and better approximations to other functions as more and more terms are kept.) ”
Fourier Transforms
An Interactive Introduction to Fourier Transforms
http://www.jezzamon.com/fourier/ (Archive)
“ Put simply, the Fourier transform is a way of splitting something up into a bunch of sine waves. As usual, the name comes from some person who lived a long time ago called Fourier....these waves look like circles when we look at them from front on. The name for the pattern of a circle moving around another circle is an epicycle. ”
Seen above: Fourier Transforms (Archive)
The Forgotten Revolution
In The Forgotten Revolution - How Science Was Born in 300 BC and Why it Had to Be Reborn, mathematician and science historian Lucio Russo (bio) relates the equivalence between Fourier and epicycle theories (Archive):
3.8 Ptolemaic Astronomy
“ The only well known Greek astronomical theory is the one Ptolemy expounds in the Almagest. We defer to Chapter 10 a comparison between early Hellenistic ideas and Ptolemy’s on such subjects as space and motion, limiting ourselves here to some observations on the mathematical model used in the Alnzagest. Everyone knows that Ptolemy’s planetary theory is based on the composition of circular motions. This technique had been used in astronomy by Apollonius of Perga, and it was in fact much older: the first algorithm of this type that we know about was worked out by Eudoxus, who described planetary motions as obtained from a succession of concentric spheres rotating uniformly, each with an axis of rotation marked by two points fixed on the previous sphere.
Because ”epicycles” is still a byword for clumsy and backward attempts at science, We spell out the two reasons why the method was supremely well-adapted to the purposes to which it was put.
First, accounting for the observed motion of planets as the composite of several uniform motions on circular orbits (the first centered on the earth and called the deferent in medieval terminology, and each of the others, called epicycles, centered on the point obtained on the preceding circumference) is equivalent to a modern expansion in Fourier series, and allows an efficient description of observed data with increasing precision as the number of epicycles grows. The analogy between Fourier series expansions and developments in epicycles was observed by Schiaparelli,135 but one can imagine that the thought occurred earlier. One can conjecture, in fact, that in this important observation Schiaparelli was preceded by the mathematicians who developed the idea of Fourier series expansions—starting with Daniel Bernoulli in the eighteenth century, who also studied planetary motion and surely knew about developments in epicycles. A formal demonstration of the equivalence has been given by Giovanni Gallavotti.136
- 135 "And we shall understand also the necessity and reason for this multiplicity of spheres, which has been wrongly criticized by those who have not grasped its function, and which arouses derision and condescension in our contemporaries, who, without knowing it, use epicycles by the dozen and by the hundreds in their planetary theories, under the name of periodical terms of infinite series” ([Schiaparelli], vol. II, p. 11).
- 136 In [Gallavotti: QPM], which also contains an interesting translation into modern mathematical terms of the main ideas from the systems of Hipparchus, Ptolemy and Copernicus. ”
Fourier, Perturbations, and Patterns
It is seen that Fourier Analysis and Perturbation Theory are used to find patterns. From Perturbation Theory in the Solar System (Archive) by theoretical physicist Carl Johnson we see:
“ In the case of the position data of a planet or any other astronomical object, if sufficient accurate data can be collected for an extended period of time, a Fourier Analysis can be done to the data. Since astronomers have been able to collect extremely precise data for at least a hundred years for most major Solar System objects, Fourier Analyses of such data generally results in many thousands of such terms. These terms are called "perturbations."
Patterns are easily seen in many of those terms, where many have periodicities (frequencies) that exactly match each other, and also match a known astronomic timing configuration. ”
Further Reference
- Math for Scientists: Refreshing the Essentials - Section 3.4.1 An Alternative Explanation of Fourier Analysis: Epicycles (Archive)
- University of Texas at El Paso paper Epicycles Are Almost as Good as Trigonometric Series: General System-Based Analysis (Archive) - "Fourier series is exactly how we now describe the visible motion of the planets (see, e.g., [1])... Epicycles are, in effect, Fourier series."
Non-Dynamical Simulations
The pertubation theory simulations are not dynamical systems. See the following:
Perturbation Theory for Restricted Three-Body Orbits
1991 Thesis by David A. Ross
I. Introduction
“ Before the astrodynamics of man-made objects in space can be fully understood, one must first comprehend basic planetary motion. Thanks to Sir Isaac Newton and his three laws of motion, and to Johann Kepler for his three laws of orbital motion, it can be shown that nearly all astrodynamical systems are dominated by a single conservative force known as gravity. In fact, the most general description of the motion of a collection of objects in space is defined by the n-body problem.
In an n-body system, the nth body is acted upon by the other n-1 gravitational masses present. In this way, the motion of any mass in a system affects and is affected by every other mass in the system. The overwhelming task of representing each body is well illustrated by Wiesel.
- "Our own solar system consists of one star, nine planets, over fifty moons, tens of thousands of asteroids, and millions of comets. The description of the motion of this system is clearly important, but an exact solution to this problem has not been found in over three hundred years of study." (8:33)
Therefore, the use of the exact n-body description of a dynamical system is not simply a nuisance, it is virtually impossible to implement. ”
Ross quotes Dr. William Weisel (bio) who admits that there is no dynamical gravity model. The dynamical way is not simply a nuisance—it is impossible and not even attempted. They are using a workaround. The paper goes on to talk about perturbation theory and fourier methods. Also see the Three Body Problem
Galactic Dynamics
It is seen that the science of the galaxies is also based on epicycles.
Lindblad’s epicycles – valid method or bad science? (Archive)
Charles Francis
“ In popular culture, epicycles have become almost synonymous with bad science; “adding epicycles” refers to a process of introducing fudges to make a theory fit data, when actually the theory needs to be replaced in its entirety. It is generally believed that epicycles were banished from science when Newton solved his equations of motion and showed that it follows from the inverse square law of gravity that planetary orbits are ellipses. So, it comes as something of a surprise to those unfamiliar with galactic dynamics that the galactic orbits of stars are treated in textbooks using a theory of epicycles revitalized by Bertil Lindblad in the 1920s, and used to introduce density wave theory, which, as reinforced by Lin & Shu (1964), by Lin, Yuan and Shu (1969) and by Kalnajs (1973), has been the leading model of spiral structure for nearly 40 years. ”
~
Conclusion
“ The implication to astrophysics is severe. The motions of stars are governed by known mathematical laws. Astrophysics is, or at least it should be, a mathematical science. One should therefore expect that theories in astrophysics are subjected to rigorous mathematical scrutiny. Regrettably, the degree of scrutiny applied to Lindblad’s epicycles and to density wave theory has been seriously lacking. Students should be made aware that these ideas can no longer be considered as science, and authors of textbooks should consider whether they merit anything more than a historical note. ”
Quotes
R. J. Morrison, F.A.S.L., R.N., in his "New Principia," says:
“ Eclipses, occultations, the positions of the planets, the motions of the fixed stars, the whole of practical navigation, the grand phenomena of the course of the sun, and the return of the comets, may all and every one of them be as accurately, nay, more accurately, known without the farrago of mystery the mathematicians have adopted to throw dust in the eyes of the people, and to claim honors to which they have no just title.
The public generally believe that the longitudes of the heavenly bodies are calculated on the principles of Newton's laws. Nothing could be more false. ”
Sir Richard Phillips in his Million Facts (Archive) reports:
“ The precision of Astronomy arises not from theories, but from prolonged observations, and the regularity of the mean motions, and the ascertained uniformity of their irregularities.
...Nothing therefore can be more impertinent than the assertion of modern writers that the accuracy of astronomical predictions arises from any modern theory. Astronomy is strictly a science of observation, and far more indebted to the false theory of Astrology, than to the equally false and fanciful theory of any modern.
We find that four or five thousand years ago, the mean motion of the Sun, Moon and Planets were known to a second, just as at present, and the moon's nodes, the latitudes of the planets, &c., were all adopted by Astrologers in preparing horoscopes for any time past or present. Ephemerides of the planet's places, of eclipses, &c., have been published for above 600 years, and were at first nearly as precise as at present. ”
The Eclipses
In Chapter 11 of Earth Not a Globe (Archive) its author gives us an overview of the eclipse calculations:
“ Those who are unacquainted with the methods of calculating eclipses and other phenomena, are prone to look upon the correctness of such calculations as powerful arguments in favour of the doctrine of the earth's rotundity and the Newtonian philosophy, generally. One of the most pitiful manifestations of ignorance of the true nature of theoretical astronomy is the ardent inquiry so often made, "How is it possible for that system to be false, which enables its professors to calculate to a second of time both solar and lunar eclipses for hundreds of years to come?" The supposition that such calculations are an essential part of the Newtonian or any other theory is entirely gratuitous, and exceedingly fallacious and misleading. Whatever theory is adopted, or if all theories are discarded, the same calculations can be made. The tables of the moon's relative positions for any fraction of time are purely practical--the result of long-continued observations, and may or may not be connected with hypothesis. The necessary data being tabulated, may be mixed up with any, even the most opposite doctrines, or kept distinct from every theory or system, just as the operator may determine.
...The simplest method of ascertaining any future eclipse is to take the tables which have been formed during hundreds of years of careful observation; or each observer may form his own tables by collecting a number of old almanacks one for each of the last forty years: separate the times of the eclipses in each year, and arrange them in a tabular form. On looking over the various items he will soon discover parallel cases, or "cycles" of eclipses; that is, taking the eclipses in the first year of his table, and examining those of each succeeding year, he will notice peculiarities in each year's phenomena; but on arriving to the items of the nineteenth and twentieth years, he will perceive that some of the eclipses in the earlier part of the table will have been now repeated--that is to say, the times and characters will be alike. If the time which has elapsed between these two parallel or similar eclipses be carefully noted, and called a "cycle," it will then be a very simple and easy matter to predict any future similar eclipse, because, at the end of the "cycle," such similar eclipse will be certain to occur; or, at least, because such repetitions of similar phenomena have occurred in every cycle of between eighteen and nineteen years during the last several thousand years, it may be reasonably expected that if the natural world continues to have the same general structure and character, such repetitions may be predicted for all future time. The whole process is neither more nor less--except a little more complicated--than that because an express train had been observed for many years to pass a given point at a given second--say of every eighteenth day, so at a similar moment of every cycle or eighteenth day, for a hundred or more years to come, the same might be predicted and expected. To tell the actual day and second, it is only necessary to ascertain on what day of the week the eighteenth or "cycle day" falls.
Tables of the places of the sun and moon, of eclipses, and of kindred phenomena, have existed for thousands of years, and were formed independently of each other, by the Chaldean, Babylonian, Egyptian, Hindoo, Chinese, and other ancient astronomers. Modern science has had nothing to do with these; farther than rendering them a little more exact, by averaging and reducing the fractional errors which a longer period of observation has detected. ”
—Samuel Rowbotham (bio)
Rowbotham also provides pattern-based equations for finding the time, magnitude, and duration of the Lunar Eclipse at the end of Chapter 11.
Royal Astronomer Robert Ball
The Royal Astronomer Sir Robert Ball (1840-1913), in his work The Story of the Heavens (Archive), on page 58, told us:
“ If we observe all the eclipses in a period of eighteen years, or nineteen years, then we can predict, with at least an approximation to the truth, all the future eclipses for many years. It is only necessary to recollect that in 6585 ⅓ days after one eclipse a nearly similar eclipse follows. For instance, a beautiful eclipse of the moon occurred on the 5th of December, 1881. If we count back 6585 days from that date, that is, 18 years and 2 days, we come to November 24th, 1863, and a similar eclipse of the moon took place then….It was this rule which enabled the ancient astronomers to predict the occurrence of eclipses at a time when the motions of the moon were not understood nearly so well as we now know them. ”
Sommerville
Somerville in Physical Sciences pg. 46 states:
“ No particular theory is required to calculate Eclipses, and the calculations may be made with equal accuracy, independent of every theory. ”
Earth Review
T.G. Ferguson in the Earth Review for September 1894, says:
“ No Doubt some will say, 'Well, how do the astronomers foretell the eclipses so accurately.' This is done by cycles. The Chinese for thousands of years have been able to predict the various solar and lunar eclipses, and do so now in spite of their disbelief in the theories of Newton and Copernicus. Keith says 'The cycle of the moon is said to have been discovered by Meton, an Athenian in B.C. 433,' then, of course, the globular theory was not dreamt of. ”
NASA Eclipse Website
Website URL: https://eclipse.gsfc.nasa.gov
If one visits NASA's eclipse website they will find that NASA explains eclipse prediction through the ancient Saros Cycle, rather than the Three Body Problem of astronomy.
From Resources -> Eclipses and the Saros (Archive) we read a description of the Saros Cycle:
“ The periodicity and recurrence of eclipses is governed by the Saros cycle, a period of approximately 6,585.3 days (18 years 11 days 8 hours). It was known to the Chaldeans as a period when lunar eclipses seem to repeat themselves, but the cycle is applicable to solar eclipses as well. ”
The reader is encouraged to visit NASA's eclipse website and count how many times the Saros Cycle is mentioned, and then count how many times the Three Body Problem is mentioned.
Google Search Term: "saros" site:https://eclipse.gsfc.nasa.gov
No. of Results: 14,400
Google Search Term: "three body" site:https://eclipse.gsfc.nasa.gov
No. of Results: 2 (duplicate text)
From the result: “ The distance of apogee does not vary by much month to month although the value of perigee can change quite a bit. Minimum vs. maximum apogee is a 0.6% spread and minimum vs. maximum perigee is a 3.9% spread. If Newton couldn't solve the three-body problem I certainly can't ”
The Three Body Problem refers to the greatest problem in the history of astronomy. It is the inability of science to simulate or recreate a model of the Sun-Earth-Moon system. It is for this reason that pattern-based methods must be used for prediction in astronomy.
Eclipse Prediction
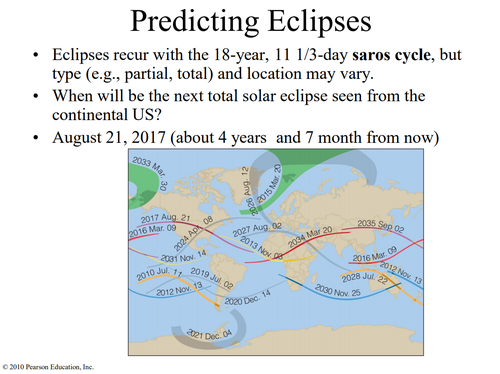
The ancient Saros Cycle method is taught in modern astronomy courses.
University of Florida
A slideshow from a University of Florida astronomy course (Archive) shows:
University College London
Under the heading How are eclipses calculated? on a University College London page by Dr. Mike Dworetsky for the Ask an Astronomer service we see only the Saros process described:
“ Thus the ancients discovered that, if a solar eclipse occurred on a given day, another eclipse would occur 6585.32 days later when the Moon and Sun again lined up almost exactly, although at a different place along the ecliptic. However, the resulting solar eclipse would be visible about 1/3 of the way around the world and not always visible from the original location, even in its partial phases. But, after three Saros cycles, or 54 years, 1 month, and a couple of days, another solar eclipse would occur at the same approximate range of longitudes on Earth. This time, however, the next eclipse in the 54 year cycle would be some distance further north or further south of the previous track, depending on whether or not the eclipses happen on the descending node (Moon going south as it crosses the ecliptic) or ascending node. ”
Exploratorium
Exploratorium.edu suggests that the method to predict the eclipse is with the Saros Cycle -
https://www.exploratorium.edu/eclipse/video/how-predict-eclipses
A Text-Book of Astronomy
Read any astronomy textbook and the same will be seen:
A TEXT-BOOK OF ASTRONOMY
by George C. Comstock
Director of the Washburn Observatory and
Professor of Astronomy in the
University of Wisconson
p.116
One should notice that there is nothing in the book about the three body problem, the geometry of the sun-earth-moon system, or Newton's equations as being the basis for the eclipse predictions.
NASA Ring Eclipse Prediction
According to NASA's Five Millennium Canon of Solar Eclipses (Archive) the Saros can predict the annular (ring eclipse), total, and hybrid types of eclipses. From p.40 we read:
“ All Saros series begin and end with a number of partial eclipses. Among the 204 Saros series with members falling within the scope of this Canon, the number of partial eclipses in the initial phase ranges from 6 to 25. Similarly, the number of partial eclipses in the final phase varies from 6 to 24. The middle life of a Saros series is composed of umbral/antumbral eclipses (i.e., annular, total, or hybrid), which range in number from 39 to 59. Table 4-3 presents the statistical distribution in the number of umbral/antumbral eclipses in the Saros series represented in the Canon. ”
NOAA Eclipse Prediction
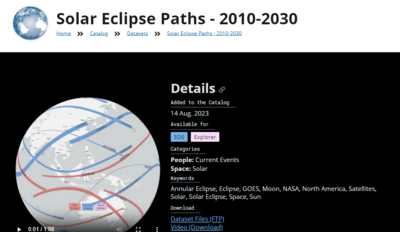
The NOAA indicates that they are using the Saros Cycle for eclipse models:
https://sos.noaa.gov/catalog/datasets/solar-eclipse-paths-2010-2030/ (Archive)
“ Eclipses are very predictable as they follow a cycle that takes place over 6,585 days. This cycle is known as the Saros cycle. Every 18 years, 11 days, and 8 hours, a similar eclipse path arises as the Sun, Earth, and Moon are relatively in the same geometry, but shifted over 120 degrees in longitude on Earth. Thanks to the cycle, we know that the path the 2023 Annular Eclipse will follow (Saros 134) will repeat on October 25, 2041, just over China and Japan. ”
Sun-Moon Epicycles
Physicist and computer scientist Stephen Wolfram (bio), creator of Wolfram Alpha, provides another assessment, regarding how the positions of the Sun and Moon are calculated with the epicycle method of prediction:
https://www.wired.com/story/when-exactly-will-the-eclipse-happen/ (Archive)
“ But computing eclipses is not exactly a new business. In fact, the Antikythera device from 2000 years ago even tried to do it—using 37 metal gears to approximate the motion of the Sun and Moon....Of course the results are a lot more accurate today. Though, strangely, despite all the theoretical science that’s been done, the way we actually compute the position of the Sun and Moon is conceptually very much like the gears—and effectively epicycles—of the Antikythera device. It’s just that now we have the digital equivalent of hundreds of thousands of gears. ”
See Also
- Three Body Problem - The heliocentric Sun-Earth-Moon system cannot be simulated
- Numerical Solutions - The available solutions for celestial systems do not fully simulate gravity
- Perturbation Methods - Epicycles are still used for astronomical prediction
- Eclipse Prediction - The eclipses are predicted with cycles and patterns
- Symplectic Integrators - A special method of orbital simulation which preserves geometry and forces stability