Difference between revisions of "Experimental Evidence"
Tom Bishop (talk | contribs) |
PeteSvarrior (talk | contribs) m (Reverted edits by 107.167.244.83 (talk) to last revision by Tom Bishop) Tag: Rollback |
||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 62: | Line 62: | ||
==The Bishop Experiment== | ==The Bishop Experiment== | ||
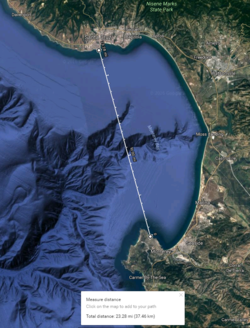
| + | [[File:Monterey.png|250px|right|thumb|Distance between the two points, courtesy of Google Earth]] | ||
| + | [[File:Pythagoras-earth.png|250px|right]] | ||
California Monterey Bay is a relatively long bay that sits next to the Pacific Ocean. The distance between the extremes of the Monterey Bay, Lovers Point in Pacific Grove and Lighthouse State Beach in Santa Cruz, is just over 23 statute miles. | California Monterey Bay is a relatively long bay that sits next to the Pacific Ocean. The distance between the extremes of the Monterey Bay, Lovers Point in Pacific Grove and Lighthouse State Beach in Santa Cruz, is just over 23 statute miles. | ||
| − | + | 0.06674 miles = 5,280 ft/mi * 0.6674 mi = 352.3872 feet | |
| + | |||
| + | Hence after 23 miles the earth drops approximately 352 feet. | ||
On a very clear and chilly day it is possible to see Lighthouse Beach from Lovers Point and vice versa. With a good telescope, laying down on the stomach at the edge of the shore near Lovers Point 20 inches above the sea level it is possible to see people at the waters edge on the adjacent beach 23 miles away near the lighthouse. The entire beach is visible down to the water splashing upon the shore. Upon looking into the telescope I can see children running in and out of the water, splashing and playing. I can see people sun bathing at the shore and teenagers merrily throwing Frisbees to one another. I can see runners jogging along the water's edge with their dogs. From my vantage point the entire beach is visible. | On a very clear and chilly day it is possible to see Lighthouse Beach from Lovers Point and vice versa. With a good telescope, laying down on the stomach at the edge of the shore near Lovers Point 20 inches above the sea level it is possible to see people at the waters edge on the adjacent beach 23 miles away near the lighthouse. The entire beach is visible down to the water splashing upon the shore. Upon looking into the telescope I can see children running in and out of the water, splashing and playing. I can see people sun bathing at the shore and teenagers merrily throwing Frisbees to one another. I can see runners jogging along the water's edge with their dogs. From my vantage point the entire beach is visible. | ||
| Line 73: | Line 77: | ||
Correcting for the height of the observer of about 20 inches, when looking at the opposite beach over 23 miles away there should be a bulge of water obscuring objects up to 300 feet above the far beach. There isn't. Even accounting for refraction, the amount hidden should be around 260 feet - seeing down to the shoreline should be impossible. | Correcting for the height of the observer of about 20 inches, when looking at the opposite beach over 23 miles away there should be a bulge of water obscuring objects up to 300 feet above the far beach. There isn't. Even accounting for refraction, the amount hidden should be around 260 feet - seeing down to the shoreline should be impossible. | ||
| − | Suppose that the earth is a sphere with a radius of 3,963 miles. If you are at a point P on the earth's surface and move tangent to the surface a distance of 1 mile then you can form a right angled triangle as in the diagram. | + | Suppose that the earth is a sphere with a radius of 3,963 miles. If you are at a point P on the earth's surface and move tangent to the surface a distance of 1 mile then you can form a right angled triangle as in the diagram (right). |
| − | Looking over a distance of 1 mile, we can use the theorem of Pythagoras: | + | Looking over a distance of 1 mile, we can use the theorem of Pythagoras (a<sup>2</sup> + b<sup>2</sup> = c<sup>2</sup>): |
| − | + | 3,963<sup>2</sup> + 1<sup>2</sup> = 15,705,370 | |
| − | and when we square root that figure we get a = 3,963.000126 miles | + | and when we square root that final figure we get a = 3,963.000126 miles |
Thus your position is 3,963.000126 - 3,963 = 0.000126 miles above the surface of the earth. | Thus your position is 3,963.000126 - 3,963 = 0.000126 miles above the surface of the earth. | ||
| − | 0.000126 miles = 12 in * 5,280 ft * 0.000126 mi = 7.98 inches | + | Converting to inches, 0.000126 miles = 12 in * 5,280 ft * 0.000126 mi = 7.98 inches |
Hence after one mile the earth drops approximately 8 inches. | Hence after one mile the earth drops approximately 8 inches. | ||
| − | |||
{{Quote | {{Quote | ||
|quote="Whenever I have doubts about the shape of the earth I simply walk outside my home, down to the beach, and perform this simple test. Provided that there is no fog and the day is clear and calm, the same result comes up over and over throughout the year." | |quote="Whenever I have doubts about the shape of the earth I simply walk outside my home, down to the beach, and perform this simple test. Provided that there is no fog and the day is clear and calm, the same result comes up over and over throughout the year." | ||
|source=Tom Bishop | |source=Tom Bishop | ||
| − | |width=40%|align= | + | |width=40%|align=right}} |
Ergo, looking across 23 miles the Pythagorean theorem becomes: | Ergo, looking across 23 miles the Pythagorean theorem becomes: | ||
| − | + | 3963<sup>2</sup> + '''23'''<sup>2</sup> = 15,705,898 | |
and when we square root that figure we get a = 3,963.06674 miles | and when we square root that figure we get a = 3,963.06674 miles | ||
| − | Thus | + | Thus the drop along c is 3,963.06674 - 3,963 (radius) = 0.06674 miles (352.3872 feet) |
| − | |||
| − | |||
| − | |||
| − | |||
| − | There are a number of different methods to calculate the drop of the Round Earth. Go ahead and look a few up to try out. You will find that the drop while looking over 23 miles is on the order of 300-400 feet. | + | There are a number of [[Round Earth Theory Curvature Calculations|different methods]] to calculate the drop of the Round Earth. Go ahead and look a few up to try out. You will find that the drop while looking over 23 miles is on the order of 300-400 feet. |
==Why I'm a Flat Earther... 37 Must-See Experiments== | ==Why I'm a Flat Earther... 37 Must-See Experiments== | ||
| Line 136: | Line 135: | ||
*Ranty Flat Earth conducts [https://www.youtube.com/channel/UC6XOkw6bHnw_tb5Iijc8LPg/videos numerous water convexity tests] on various lakes and ocean inlets such as the Irish Sea. Ranty often sees windows and details on buildings from a [https://www.youtube.com/watch?v=jKUSz46h2is distance of 18.5+ miles] away at an elevation of 4 feet with a P1000 camera. Ranty even brings his camera [https://www.youtube.com/watch?v=WyjHExZDMV8down to 2 inches above the water line.] | *Ranty Flat Earth conducts [https://www.youtube.com/channel/UC6XOkw6bHnw_tb5Iijc8LPg/videos numerous water convexity tests] on various lakes and ocean inlets such as the Irish Sea. Ranty often sees windows and details on buildings from a [https://www.youtube.com/watch?v=jKUSz46h2is distance of 18.5+ miles] away at an elevation of 4 feet with a P1000 camera. Ranty even brings his camera [https://www.youtube.com/watch?v=WyjHExZDMV8down to 2 inches above the water line.] | ||
*[https://youtu.be/6J37b8-rsic "Fox News Confirms Flat Earth from Michigan to Milwaukee"] | *[https://youtu.be/6J37b8-rsic "Fox News Confirms Flat Earth from Michigan to Milwaukee"] | ||
| + | *[https://www.youtube.com/watch?v=wL0EyEraT3s&ab_channel=FlatandStationary Black Swan: 9.41 Mile Earth Curvature Test, Platform Habitat / Hillhouse. Santa Barbara, CA.] | ||
</div> | </div> | ||
Latest revision as of 17:23, 15 October 2022
The following sections contain experimental evidence in favor of a Flat Earth.
Water Convexity Experiments
The Bedford Canal Experiments
The classic Flat Earth water convexity experiments were described in the book Earth Not a Globe by Samuel Birley Rowbotham. Rowbotham lives near the canal and performs the experiment numerous times over a long period of time. The Bedford Canal is a man-made canal which was selected as the most ideal location for the types of experiments performed due to the narrow passageways and low disturbance of the water's surface.
Of special interest, and in regards to the popularized subject of refraction, we look at the second experiment in the text.
Experiment Two
From Experiment Two of Earth Not a Globe we read:
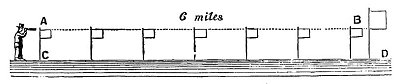
- “ Along the edge of the water, in the same canal, six flags were placed, one statute mile from each other, and so arranged that the top of each flag was 5 feet above the surface. Close to the last flag in the series a longer staff was fixed, bearing a flag 3 feet square, and the top of which was 8 feet above the surface of the water--the bottom being in a line with the tops of the other and intervening flags, as shown in the following diagram, Fig, 4. ”
- “ On looking with a good telescope over and along the flags, from A to B, the line of sight fell on the lower part of the larger flag at B. The altitude of the point B above the water at D was 5 feet, and the altitude of the telescope at A above the water at C was 5 feet; and each intervening flag had the same altitude. Hence the surface of the water C, D, was equidistant from the line of sight A, B; and as A B was a right line, C, D, being parallel, was also a right line; or, in other words, the surface of the water, C, D, was for six miles absolutely horizontal.
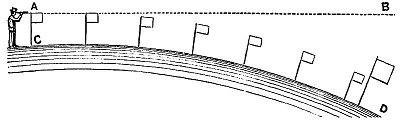
- If the earth is a globe, the series of flags in the last experiment would have had the form and produced the results represented in the diagram, Fig. 5. The water curvating from ”
- “ C to D, each flag would have been a given amount below the line A, B. The first and second flags would have determined the direction of the line of sight from A to B, and the third flag would have been 8 inches below the second; the fourth flag, 32 inches; the fifth, 6 feet; the sixth, 10 feet 8 inches; and the seventh, 16 feet 8 inches; but the top of the last and largest flag, being 3 feet higher than the smaller ones, would have been 13 feet 8 inches below the line of sight at the point B. ”
On analysis of this experiment, if the earth were a globe, one important remark would be that it is quite the coincidence that the flags all experienced the Flat Earth refraction effect, one by one, all the way down to the end, which projected each flag into the air at the exact height they needed to be at in order to make things look flat in accordance with the distance looked across and the height of the observer.
There are multiple control points in this experiment and others. Each point is a test in the experiment. Incredible refraction coincidences would need to occur to account for them. The top of the first flag would have to have been projected 8 inches into the air, the second flag 2.67 feet, the third flag 6 feet, the fourth flag 10.6 feet, the fifth flag 14.29 feet, and the sixth flag 24.01 feet into the air, when the later flags should be below the horizon. Rowbotham is well aware of the "it was refraction" argument, and his experiment is designed to test the refraction of light rays on the flags of constant height against the taller flag at the end. The observation is artificially manipulated—controlled—to separate one explanation from another, in the effort to more truthfully determine a cause of an observation.
Similar Experiments
Modern versions of the multi-point experiments like Experiment Two above have been conducted.
- Four Light Rock Lake Manitoba Test (Archive) - Runtime: 3m23s (Full Length Source Vid)
- Hernando County Waterways - Runtime: 2m34s (Navigational Marker Locations)
Other ENAG Experiments
- Experiment 1 - Boat Unsunken, 6 miles (Two Point)
- Experiment 3 - Theodolite Between Bridges (Three Point)
- Experiment 4 - Theodolite-Flag-Cross (Three Point)
- Experiment 5 - Bridge Notice Board (Two Point)
- Experiment 6 - Receding Boat (Duration type, Multiple Points)
- Experiment 7 - Horizontal Curvature - Long Board
- Experiment 8 - Horizontal Curvature - Crosshair
- Experiment 9 - Boat Between Lighthouses (Three Point)
- Experiment 1 - Boat Unsunken, 6 miles (Two Point)
Repetitions
The Bedford Level Experiment was reproduced by Lady Blount and others. See the Bedford Level Experiment
Weather and Wave Conditions
In the chapter On the Dimensions of Ocean Waves, Rowbotham explains that the above is affected by wind and water conditions. The reproduction works best in fine weather:
- “ It is well known that even on lakes of small dimensions and also on canals, when high winds prevail for some time in the same direction, the ordinary ripple is converted into comparatively large waves. On the "Bedford Canal," during the windy season, the water is raised into undulations so high, that through a powerful telescope at an elevation of 8 inches, a boat two or three miles away will be invisible; but at other times, through the same telescope the same kind of boat may be seen at a distance of six or eight miles.
- During very fine weather when the water has been calm for some days and become as it were settled down, persons are often able to see with the naked eye from Dover the coast of France, and a steamer has been traced all the way across the channel. At other times when the winds are very high, and a heavy swell prevails, the coast is invisible, and the steamers cannot be traced the whole distance from the same altitude, even with a good telescope.
- Instances could be greatly multiplied, but already more evidence has been given than the subject really requires, to prove that when a telescope does not restore the hull of a distant vessel it is owing to a purely special and local cause. ”
The Bishop Experiment
California Monterey Bay is a relatively long bay that sits next to the Pacific Ocean. The distance between the extremes of the Monterey Bay, Lovers Point in Pacific Grove and Lighthouse State Beach in Santa Cruz, is just over 23 statute miles.
0.06674 miles = 5,280 ft/mi * 0.6674 mi = 352.3872 feet
Hence after 23 miles the earth drops approximately 352 feet.
On a very clear and chilly day it is possible to see Lighthouse Beach from Lovers Point and vice versa. With a good telescope, laying down on the stomach at the edge of the shore near Lovers Point 20 inches above the sea level it is possible to see people at the waters edge on the adjacent beach 23 miles away near the lighthouse. The entire beach is visible down to the water splashing upon the shore. Upon looking into the telescope I can see children running in and out of the water, splashing and playing. I can see people sun bathing at the shore and teenagers merrily throwing Frisbees to one another. I can see runners jogging along the water's edge with their dogs. From my vantage point the entire beach is visible.
IF the earth is a globe, and is 24,900 English statute miles in circumference, the surface of all standing water must have a certain degree of convexity--every part must be an arc of a circle. From the summit of any such arc there will exist a curvature or declination of 8 inches over the first statute mile. Over two miles the fall will be 32 inches; by the end of the third mile, 72 inches, or 6 feet, as shown in this chart.
Correcting for the height of the observer of about 20 inches, when looking at the opposite beach over 23 miles away there should be a bulge of water obscuring objects up to 300 feet above the far beach. There isn't. Even accounting for refraction, the amount hidden should be around 260 feet - seeing down to the shoreline should be impossible.
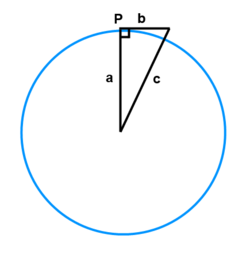
Suppose that the earth is a sphere with a radius of 3,963 miles. If you are at a point P on the earth's surface and move tangent to the surface a distance of 1 mile then you can form a right angled triangle as in the diagram (right).
Looking over a distance of 1 mile, we can use the theorem of Pythagoras (a2 + b2 = c2):
3,9632 + 12 = 15,705,370
and when we square root that final figure we get a = 3,963.000126 miles
Thus your position is 3,963.000126 - 3,963 = 0.000126 miles above the surface of the earth.
Converting to inches, 0.000126 miles = 12 in * 5,280 ft * 0.000126 mi = 7.98 inches
Hence after one mile the earth drops approximately 8 inches.
|
Ergo, looking across 23 miles the Pythagorean theorem becomes:
39632 + 232 = 15,705,898
and when we square root that figure we get a = 3,963.06674 miles
Thus the drop along c is 3,963.06674 - 3,963 (radius) = 0.06674 miles (352.3872 feet)
There are a number of different methods to calculate the drop of the Round Earth. Go ahead and look a few up to try out. You will find that the drop while looking over 23 miles is on the order of 300-400 feet.
Why I'm a Flat Earther... 37 Must-See Experiments
The Flat Earth movement performs continuous validation and checks of Earth Not a Globe by Samuel Birley Rowbotham. The following is a good collection of experiments which demonstrate a Flat Earth (Runtime: 2 Hours).
Sinking Ship Effect
The Sinking Ship Effect is often used as evidence of the earth's rotundity. It was one of the first proofs of Aristotle and other philosophers. It was based primarily upon this phenomenon that the earth was declared by the ancients to be globular. It has been found that when the phenomenon is studied with modern methods, such as through long period time-lapse photography, that the Sinking Ship Effect is not consistent. The effect appears to come and go over time. See: Sinking Ship Effect Caused By Refraction
Further Flat Earth Evidence
- Flat Earth v. Sinking Comparison
Ben, Taboo Conspiracy, reports that sometimes he is able to see further than the curvature of the earth should allow, and at other times things appear sunken. He compares the two scenes. In his comparison the sunken scene was more distorted than the flat earth scene. Does refraction make things blurrier or clearer? - Video: Monterey Bay Experiment over 13.23 Miles shows a Flat Earth.
- A woman named Lady Blount was among the first to peer review Rowbotham's work: Lady Blount Trials
- Pier2Pier Dr. John D - 9.5 mi two-way laser test
- Jeran Flat Earth Experiment 4 Mile Laser Test
- 7.5 Mile Flat Earth Laser Test On Frozen Lake
- Grouataone - 7.4 Mile Frozen Lake Test
- Flat Earth Perth - 15 km Laser Test Mandurah
- DMarble 10 Mile Laser Test
- 16.4 Mile Laser Test
- Flat Earth - Islands Seen 31.6 Miles From Miramar Beach
- Platform Habitat / Hillhouse at 9.41 Miles. -- No loss of visibility due to Earth's curvature when changing altitude.
- Salton Sea Level Observation 9.77 Miles No curvature
- "Flat Earther proves no curvature at Salton Sea. Leaves Scientists baffled" -- Conducted in association with the Independent Investigations Group
- Ranty Flat Earth conducts numerous water convexity tests on various lakes and ocean inlets such as the Irish Sea. Ranty often sees windows and details on buildings from a distance of 18.5+ miles away at an elevation of 4 feet with a P1000 camera. Ranty even brings his camera to 2 inches above the water line.
- "Fox News Confirms Flat Earth from Michigan to Milwaukee"
- Black Swan: 9.41 Mile Earth Curvature Test, Platform Habitat / Hillhouse. Santa Barbara, CA.