Difference between revisions of "Distance to the Sun"
Tom Bishop (talk | contribs) |
Tom Bishop (talk | contribs) |
||
| (52 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | The distance to the Sun and celestial bodies under the Flat Earth model varies depending on the assumptions used. Under the celestial model of '''[[Electromagnetic Acceleration]]''' where light curves, the Sun and celestial bodies can be estimated to be about 6000 miles above the surface of the Earth. Under a straight-line model, the Sun can be estimated to be about 3000 miles above the surface of the Earth. | |
| − | The | + | The purpose of this page is to showcase the historic methods that have been used to determine the height of the sun and celestial bodies. Of special interest, this page will show that the Round Earth distance to the sun, and therefore the size of the solar system, relies on the idea that the earth is a sphere. The triangulation method depends on an assumption about the shape of the earth. |
| − | + | ==EA Model Estimate== | |
| − | == | + | If '''[[Electromagnetic Acceleration]]''' is considered, the celestial bodies are possibly about 6000 miles in altitude, which can be deduced using the North Star under the following axioms: |
| + | |||
| + | *The North Star is directly over the North Pole | ||
| + | *The conventional distance from the North Pole to the Equator is correct | ||
| + | *The celestial bodies descend consistently in the sky with the distance you recede away from them | ||
| + | *The light from the celestial bodies behave in generally the same way, and so must be in layers near to each other | ||
| + | |||
| + | From the position of the North Pole where the North Star is directly overhead, to the position of the Equator which is defined as where the North Star is seen at the horizon, the distance between the points is approximately 6000 miles according to conventional figures. Over that distance, if through EA the North Star is seen to descend or ascend in the sky consistently with consistent distance, then we know that the altitude of the North Star above the Earth is consistent with the distance between the North Pole and the equator. At the North Pole the North Star is approximately 6000 miles above the the surface of the Earth. | ||
| + | |||
| + | ==Round Earth vs. Flat Earth== | ||
'''Q.''' Why are the celestial bodies and the sun so close to the earth's surface in the Flat Earth Model? | '''Q.''' Why are the celestial bodies and the sun so close to the earth's surface in the Flat Earth Model? | ||
| − | '''A.''' The celestial bodies must be close because if the shape of the earth changes, the distance to the celestial bodies must change as well. Astronomers use two different observations on far off points on earth to triangulate the distance of celestial bodies. When the shape of the earth changes, the triangulation changes, and our perception of the universe must therefore change as well. | + | '''A.''' The celestial bodies must be close because if the shape of the earth changes from round to flat, the distance to the celestial bodies must change as well. Astronomers use two different observations on far off points on earth to triangulate the distance of celestial bodies. When the shape of the earth changes, the triangulation changes, and our perception of the universe must therefore change as well. |
Eratosthenes' stick experiment can not only tell us about the size of the earth, but can also be used to compute the distance to the sun as well. If the earth is round, the celestial bodies are computed to be millions of miles distant. If the earth is flat, the celestial bodies are triangulated to be relatively close to the earth's surface. | Eratosthenes' stick experiment can not only tell us about the size of the earth, but can also be used to compute the distance to the sun as well. If the earth is round, the celestial bodies are computed to be millions of miles distant. If the earth is flat, the celestial bodies are triangulated to be relatively close to the earth's surface. | ||
| Line 19: | Line 28: | ||
Here's a link which explains the idea: http://www.millersville.edu/physics/experiments/058/index.php. The first part goes over the Round Earth explanation for how the sun can be computed millions of miles distant. At the bottom there is a Flat Earth explanation for how the sun can be computed as being very close to the earth's surface. Scroll all the way to the bottom to the "alternative model" section. You will find that we can use Eratosthenes' data, in conjunction with the assumption of a Flat Earth, to confirm that in FET the sun is very near to the earth's surface. | Here's a link which explains the idea: http://www.millersville.edu/physics/experiments/058/index.php. The first part goes over the Round Earth explanation for how the sun can be computed millions of miles distant. At the bottom there is a Flat Earth explanation for how the sun can be computed as being very close to the earth's surface. Scroll all the way to the bottom to the "alternative model" section. You will find that we can use Eratosthenes' data, in conjunction with the assumption of a Flat Earth, to confirm that in FET the sun is very near to the earth's surface. | ||
| − | Hence, | + | Hence, if we assume that the earth is flat and that slight travels in straight lines, triangles and trigonometry can demonstrate that the celestial bodies are fairly close to the earth. |
| − | + | {{cite|Eratosthenes' model depends on the assumption that the earth is a globe and that the sun is far away and therefore produces parallel rays of light all over the earth. If the sun is nearby, then shadows will change length even for a flat earth. A flat earth model is sketched below. The vertical stick casts shadows that grow longer as the stick moves to the left, away from the closest point to the sun. (The sun is at height h above the earth.}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[File:flatrth.png|300px]] | |
| − | + | {{cite|A little trigonometry shows that}} | |
| − | + | [[File:flateqn.png|300px]] | |
| − | + | {{cite|Using the values 50 degrees and 60 degrees as measured on the trip, with b=1000 miles, we find that h is approximately 2000 miles. This relatively close sun would have been quite plausible to the ancients. | |
| − | + | ||
| − | + | Continuing the calculation, we find that a is approximately 2400 miles and the two distances R1 and R2 are approximately 3000 and 3900 miles, respectively.}} | |
| − | |||
| − | |||
| − | |||
There is no other way to get a distance for the sun. Just looking at it from a single point on earth will not tell you its distance, you must look at it from several points and account for the curvature or non-curvature of the distance between those points. | There is no other way to get a distance for the sun. Just looking at it from a single point on earth will not tell you its distance, you must look at it from several points and account for the curvature or non-curvature of the distance between those points. | ||
| Line 45: | Line 46: | ||
Please note: The writer of that article makes a unrelated side comment about the Flat Earth model -- | Please note: The writer of that article makes a unrelated side comment about the Flat Earth model -- | ||
| − | + | {{cite|That is, as we move from Florida to Pennsylvania, our distance from the sun increases by about 30%. As a consequence the apparent size of the sun should decrease by 30%. We see no noticeable change in the apparent size of the sun as we make the trip. We conclude that the flat earth/near sun model does not work.}} | |
| − | |||
| − | |||
| − | |||
| − | This has | + | This has little to do with the distance from the sun via triangulation methods. The writer of the above statement apparently did not read Chapter 10 of Earth Not a Globe. See: [[Magnification of the Sun at Sunset]] |
== Sun's Distance - Zetetic Cosmogony == | == Sun's Distance - Zetetic Cosmogony == | ||
| − | Thomas Winship, author of Zetetic Cosmogony, provides a calculation demonstrating that the sun can be computed to be relatively close to the earth's surface if one assumes that the earth is flat -- | + | Thomas Winship, author of Zetetic Cosmogony, provides a calculation demonstrating that the sun can be computed to be relatively close to the earth's surface if one assumes that the earth is flat and that light travels in straight lines -- |
| − | + | {{cite|On March 21-22 the sun is directly overhead at the equator and appears 45 degrees above the horizon at 45 degrees north and south latitude. As the angle of sun above the earth at the equator is 90 degrees while it is 45 degrees at 45 degrees north or south latitude, it follows that the angle at the sun between the vertical from the horizon and the line from the observers at 45 degrees north and south must also be 45 degrees. The result is two right angled triangles with legs of equal length. The distance between the equator and the points at 45 degrees north or south is approximately 3,000 miles. Ergo, the sun would be an equal distance above the equator.}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Sun's Distance - Modern Mechanics == | == Sun's Distance - Modern Mechanics == | ||
| − | Modern Mechanics describes how on a Flat Earth the sun can be computed to 3,000 miles via triangulation, whereas on a globe earth those same angles can calculate the sun to nearly 93 million miles away -- | + | Modern Mechanics describes how on a Flat Earth the sun can be computed to 3,000 miles via straight line triangulation, whereas on a globe earth those same angles can calculate the sun to nearly 93 million miles away -- |
[[File:Xlg_globe_3.jpg|500px]] | [[File:Xlg_globe_3.jpg|500px]] | ||
| − | [http://blog.modernmechanix.com/2006/05/19/5000-for-proving-the-earth-is-a-globe/ | + | [https://web.archive.org/web/20120205001209/http://blog.modernmechanix.com/2006/05/19/5000-for-proving-the-earth-is-a-globe/ $5,000 for Proving the Earth is a Globe] (Modern Mechanics - Oct, 1931) |
== See also == | == See also == | ||
*[[Magnification of the Sun at Sunset]] | *[[Magnification of the Sun at Sunset]] | ||
| + | |||
| + | [[Category:Cosmos]] | ||
[[Category:Sun]] | [[Category:Sun]] | ||
| + | [[Category:Parallax]] | ||
Latest revision as of 00:56, 27 September 2023
The distance to the Sun and celestial bodies under the Flat Earth model varies depending on the assumptions used. Under the celestial model of Electromagnetic Acceleration where light curves, the Sun and celestial bodies can be estimated to be about 6000 miles above the surface of the Earth. Under a straight-line model, the Sun can be estimated to be about 3000 miles above the surface of the Earth.
The purpose of this page is to showcase the historic methods that have been used to determine the height of the sun and celestial bodies. Of special interest, this page will show that the Round Earth distance to the sun, and therefore the size of the solar system, relies on the idea that the earth is a sphere. The triangulation method depends on an assumption about the shape of the earth.
EA Model Estimate
If Electromagnetic Acceleration is considered, the celestial bodies are possibly about 6000 miles in altitude, which can be deduced using the North Star under the following axioms:
- The North Star is directly over the North Pole
- The conventional distance from the North Pole to the Equator is correct
- The celestial bodies descend consistently in the sky with the distance you recede away from them
- The light from the celestial bodies behave in generally the same way, and so must be in layers near to each other
From the position of the North Pole where the North Star is directly overhead, to the position of the Equator which is defined as where the North Star is seen at the horizon, the distance between the points is approximately 6000 miles according to conventional figures. Over that distance, if through EA the North Star is seen to descend or ascend in the sky consistently with consistent distance, then we know that the altitude of the North Star above the Earth is consistent with the distance between the North Pole and the equator. At the North Pole the North Star is approximately 6000 miles above the the surface of the Earth.
Round Earth vs. Flat Earth
Q. Why are the celestial bodies and the sun so close to the earth's surface in the Flat Earth Model?
A. The celestial bodies must be close because if the shape of the earth changes from round to flat, the distance to the celestial bodies must change as well. Astronomers use two different observations on far off points on earth to triangulate the distance of celestial bodies. When the shape of the earth changes, the triangulation changes, and our perception of the universe must therefore change as well.
Eratosthenes' stick experiment can not only tell us about the size of the earth, but can also be used to compute the distance to the sun as well. If the earth is round, the celestial bodies are computed to be millions of miles distant. If the earth is flat, the celestial bodies are triangulated to be relatively close to the earth's surface.
In his experiment Eratosthenes assumes that the earth is a globe and that the sun is very far away in his computations for the size of the earth and the distance to the sun. However, if we use his data with the assumption that the earth is flat we can come up with a wildly different calculation for the distance of the sun, showing it to be close to the earth. The sun changes its distance depending on the model of the earth we assume for the experiment.
Millersville University goes over the two ways of interpreting Eratosthenes' data. The first part of the article goes over the interpretation of his data under a Round Earth model, and the bottom part of the article goes over an interpretation of the data under a Flat Earth model.
Here's a link which explains the idea: http://www.millersville.edu/physics/experiments/058/index.php. The first part goes over the Round Earth explanation for how the sun can be computed millions of miles distant. At the bottom there is a Flat Earth explanation for how the sun can be computed as being very close to the earth's surface. Scroll all the way to the bottom to the "alternative model" section. You will find that we can use Eratosthenes' data, in conjunction with the assumption of a Flat Earth, to confirm that in FET the sun is very near to the earth's surface.
Hence, if we assume that the earth is flat and that slight travels in straight lines, triangles and trigonometry can demonstrate that the celestial bodies are fairly close to the earth.
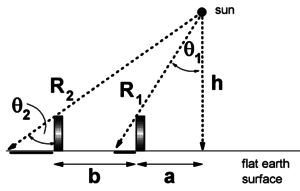
“ Eratosthenes' model depends on the assumption that the earth is a globe and that the sun is far away and therefore produces parallel rays of light all over the earth. If the sun is nearby, then shadows will change length even for a flat earth. A flat earth model is sketched below. The vertical stick casts shadows that grow longer as the stick moves to the left, away from the closest point to the sun. (The sun is at height h above the earth. ”
“ A little trigonometry shows that ”
“ Using the values 50 degrees and 60 degrees as measured on the trip, with b=1000 miles, we find that h is approximately 2000 miles. This relatively close sun would have been quite plausible to the ancients.
Continuing the calculation, we find that a is approximately 2400 miles and the two distances R1 and R2 are approximately 3000 and 3900 miles, respectively. ”
There is no other way to get a distance for the sun. Just looking at it from a single point on earth will not tell you its distance, you must look at it from several points and account for the curvature or non-curvature of the distance between those points.
Please note: The writer of that article makes a unrelated side comment about the Flat Earth model --
“ That is, as we move from Florida to Pennsylvania, our distance from the sun increases by about 30%. As a consequence the apparent size of the sun should decrease by 30%. We see no noticeable change in the apparent size of the sun as we make the trip. We conclude that the flat earth/near sun model does not work. ”
This has little to do with the distance from the sun via triangulation methods. The writer of the above statement apparently did not read Chapter 10 of Earth Not a Globe. See: Magnification of the Sun at Sunset
Sun's Distance - Zetetic Cosmogony
Thomas Winship, author of Zetetic Cosmogony, provides a calculation demonstrating that the sun can be computed to be relatively close to the earth's surface if one assumes that the earth is flat and that light travels in straight lines --
“ On March 21-22 the sun is directly overhead at the equator and appears 45 degrees above the horizon at 45 degrees north and south latitude. As the angle of sun above the earth at the equator is 90 degrees while it is 45 degrees at 45 degrees north or south latitude, it follows that the angle at the sun between the vertical from the horizon and the line from the observers at 45 degrees north and south must also be 45 degrees. The result is two right angled triangles with legs of equal length. The distance between the equator and the points at 45 degrees north or south is approximately 3,000 miles. Ergo, the sun would be an equal distance above the equator. ”
Sun's Distance - Modern Mechanics
Modern Mechanics describes how on a Flat Earth the sun can be computed to 3,000 miles via straight line triangulation, whereas on a globe earth those same angles can calculate the sun to nearly 93 million miles away --
$5,000 for Proving the Earth is a Globe (Modern Mechanics - Oct, 1931)