Atlas Burdened to Carry the Heavens —
The Cosmographicall Glasse, 1559It has been asserted many times, and with great insistence, that astronomers can simulate and predict the positions of the bodies in the Solar System for any given time with the Round Earth Theory of the Solar System. Because of this, it is powerful evidence that the system of the Round Earth Theory is true. Kepler's Laws, Newton's Laws, with other Celestial Mechanics equations and resources, are presented as undeniable fact. It is presented in that manner to children in school, in popular culture, and this assertion is seen by our society on a near daily basis.
The system of the Round Earth Theory has been verified and validated through astronomical and mathematical prediction, as the story goes, and anyone who dare speak a word otherwise is a fool.
Readers of history and astronomy, however, will know that this is not how astronomers predict the location of bodies in the sky. The bodies are not predicted based on any heliocentric construct of the solar system and orbits. Prediction in astronomy is based solely on patterns in the sky. Celestial events come in patterns and trends. By analyzing the patterns from past behaviors from historic tables it is possible to create an equation that will predict a future event. This is how prediction in astronomy has been performed for thousands of years, and how it is still performed today.
Thomas Winship provides the following—
"Sir Richard Phillips in his Million Facts, says, 'Nothing therefore can be more impertinent than the assertion of modern writers that the accuracy of astronomical predictions arises from any modern theory. Astronomy is strictly a science of observation, and far more indebted to the false theory of Astrology, than to the equally false and fanciful theory of any modern.
We find that four or five thousand years ago, the mean motion of the Sun, Moon and Planets were known to a second, just as at present, and the moon's nodes, the latitudes of the planets, &c., were all adopted by Astrologers in preparing horoscopes for any time past or present. Ephemerides of the planet's places, of eclipses, &c., have been published for above 600 years, and were at first nearly as precise as at present.'"
The above quote speaks for itself. It is true now as it has ever been.
It may come as a shock to learn that Celestial Mechanics, whether in the days of Kepler, or in its form today, cannot actually predict the placement of any body in the solar system at all. The many computer software applications that predict the locations of the planets are not doing so based on orbital motions in a heliocentric system.
It may come as a greater shock to learn that not only are they unable to predict, they are unable to even model or simulate the basic motions of the solar system based on the heliocentric theory, even on a fundamental level.
We will look at works by professionals in the field who will explain why Celestial Mechanics cannot model the solar system. Who better to consult than those who have labored to predict with the system?
Modern Celestial Mechanics
MODERN CELESTIAL MECHANICS
Aspects of Solar System Dynamics
By Alessandro Morbidelli, PhD
PDF Link
This book begins its introduction by describing Celestial Mechanics as a wonderful and successful tool for the theory of the structure and evolution of the Solar System.
From the first sentence:
In the last 20 years, Celestial Mechanics has achieved spectacular results on the structure and evolution of our Solar System.
—Modern Celestial Mechanics
|
After the triumphing the success of theory to predict theory, the author, a Mathematician, provides a background on Celestial Mechanics and its ability to predict reality.
The first attempts to predict the motion of the planets in the sky date back to the dawn of civilization. However, what is now properly called Celestial Mechanics was born with Newton’s announcement (1687) of the law of universal gravitation. Since then, the computation of precise ephemerides has become essentially a mathematical challenge. Lagrange and Laplace particularly distinguished themselves in this search at the end of the XVIIIth century. To obtain increasing accuracy, they designed the first step of the theory of secular motion of planetary orbits, and the latter also understood the importance of a quasi-resonance between the orbital periods of Jupiter and Saturn. At that time, every apparent anomaly in planetary motion seemed to be accountable by a sufficiently accurate theory based on Newtonian gravitation. This success forged Laplace’s absolute faith in determinism, which then characterized the whole science of the XIXth century. The search for increasingly accurate analytic ephemerides has been continuing through the centuries up to the present time. But two centuries later than Laplace’s work – after the discovery of a new phenomenon called chaos, the introduction of the first numerical methods for its detection and the construction of powerful computers – it was pointed out that the motion of the planets is in fact chaotic. Since then, a major goal of Celestial Mechanics has been to understand the reasons for this chaotic motion, and its consequences for the long-term evolution of the planetary system.
—Modern Celestial Mechanics
|
The reader is informed that Celestial Mechanics is not, and has never been, successful at predicting the positions of planets.
A further definition is given for "chaotic":
the considered orbit is chaotic, if we intend the word chaos as a synonym for irregular and unpredictable behavior
—Modern Celestial Mechanics
|
Another description:
Because of the existence of chaos, which makes the motion unpredictable on timescales of several times the inverse of the Lyapunov exponent (5 My), the results of these integrations should be regarded only as representative of possible evolutions; however, as seen in the simple numerical examples of Chapter 4, numerical integrationmay give an indication of the extent of the chaotic region that is reachable over the integration time.
—Modern Celestial Mechanics
|
Chaos and the Solar System
In Chaos and the Solar System by Paul Trow a good history and description of Chaos Theory is given, with further clarification on the issue of modeling the behavior of seemingly simple systems.
Chaos and the Solar System
by Paul Trow
Article Link
What exactly is chaos? We can give an example by a rigid pendulum, such as in a grandfather clock. If the pendulum swings freely, its motion will be perfectly regular and periodic, and if there were no friction, it would continue this way forever. The system is perfectly predictable – it is the opposite of chaos. But now suppose that we place an electric magnet at the base of the pendulum, and arrange for the magnet turn on momentarily at regular intervals – say once every second – at which time it exerts a magnetic force on the pendulum. This device is rather like a parent pushing a child on a swing, but unlike the parent who pushes in time with the swing, the magnet’s forces are out of phase with the pendulum. If the magnet exerts its force during the pendulum’s downward swing, it speeds the pendulum up – but if it does so during the upward swing, it slows the pendulum down. The question is simply this: what will happen to the pendulum? Will it swing regularly or irregularly? Can we predict its motion at all?
Since the device is such a simple deterministic system, and the magnet’s push occurs at regular intervals, we might guess that the pendulum’s motion would be periodic. In other words, after a while the motion would begin to repeat itself. Surprisingly, what actually happens is that the pendulum begins to swing irregularly, sometimes higher and sometimes lower, without any discernible pattern. We are no more able to predict how high the pendulum will go after a few swings than we are to predict the outcome of a roll of the dice. What this device shows is that a simple deterministic mechanism can generate what appears to be random motion – in other words, it is chaotic.
There is a historical irony in the fact that this simple device is chaotic. Galileo studied the motion of freely swinging pendulums, and discovered that their period is independent of the length of the pendulum. Indeed, this discovery, along with his famous analysis of falling bodies and projectiles, were some of the first quantitative descriptions of terrestrial motion. Galileo’s work was one of the two most significant influences on Newton’s thinking. The irony is that something so simple as a pendulum – the very symbol of the deterministic universe – can be altered so slightly as to produce chaos. And the historical question this raises is why it took almost three hundred for someone to recognize the possibility of chaotic motion. I think it is safe to say that because Galileo and the other great genius of the scientific revolution were searching for order in the universe, they were blind to the existence of chaos all around them.
—Chaos and the Solar System
|
The author goes on, describing that the motion of planetary systems has been an issue for a long time.
Describing the motion of any planetary system (including purely imaginary ones that exist only on paper) is the subject of a branch of mathematics called celestial mechanics. Its problems are extremely difficult and have eluded the greatest mathematicians in history.
—Chaos and the Solar System
|
The mathematician and theoretical physicist Henri Poincaré was instrumental in showcasing the challenges of Celestial Mechanics:
As other mathematicians had done before, Poincaré considered a special case in which there are just three planetary bodies (the so-called three-body problem). Poincaré, however, tried a novel approach to the problem: rather than trying to explicitly solve the equations of motion, as mathematicians had always done previously, he looked at the qualitative behavior of planetary orbits - for example, whether they were periodic or followed more irregular paths. This approach had a liberating effect, enabling him to see possibilities that others had overlooked. What he discovered was quite unexpected: the motion of a planet in a three-body system can be very wild and unpredictable indeed. Its orbit can follow an apparently random curve, winding back around itself over and over again, like a long and tangled string. As he described such curves:
When one tries to depict the figure formed by these two curves and their infinity of intersections, each of which corresponds to a doubly asymptotic solution, these intersections form a kind of net, web, or infinitely tight mesh; neither of the two curves can ever cross itself, but must fold back on itself in a very complex way … Nothing can give us a better idea of the complexity of the three-body problem.
—Chaos and the Solar System
|
The article continues:
Poincaré’s discovery was surprising because it contradicted age-old assumptions about the motion of the planets. Beginning with the early Greeks, who thought that the planets moved in circles, astronomers had long believed that planetary motion was built up from simple motion. The theories of Kepler and Newton reinforced this belief. Before Poincaré, no one had imagined that such complicated, unpredictable motion could occur in the solar system. It must have come as a shock to him to realize that the motion of a planet could appear to be as random as that in a pinball machine.
—Chaos and the Solar System
|
From 'Mathematics Applied to Deterministic Problems in Natural Sciences' we read another account of Poincare's discoveries:
As Poincare experimented, he was relieved to discover that in most of the situations, the possible orbits varied only slightly from the initial 2-body orbit, and were still stable, but what occurred during further experimentation was a shock. Poincare discovered that even in some of the smallest approximations some orbits behaved in an erratic unstable manner. His calculations showed that even a minute gravitational pull from a third body might cause a planet to wobble and fly out of orbit all together.
—Mathematics
|
The Best of the Best
The analytical solution to the three-body problem is the ability to predict where bodies will be based on starting parameters, which is admitted to be impossible.
The numerical solution to the three body problem is essentially the ability to model or simulate where bodies will be, by accounting for the gravitational influences of the bodies at small incremental time steps.
In such simulations the orbits of three bodies with unequal masses will fly apart, and the available solutions to the numerical three body problem assume unrealistic scenarios-- such as the Restricted Three Body Problem, which assumes that one of the bodies is mass-less.
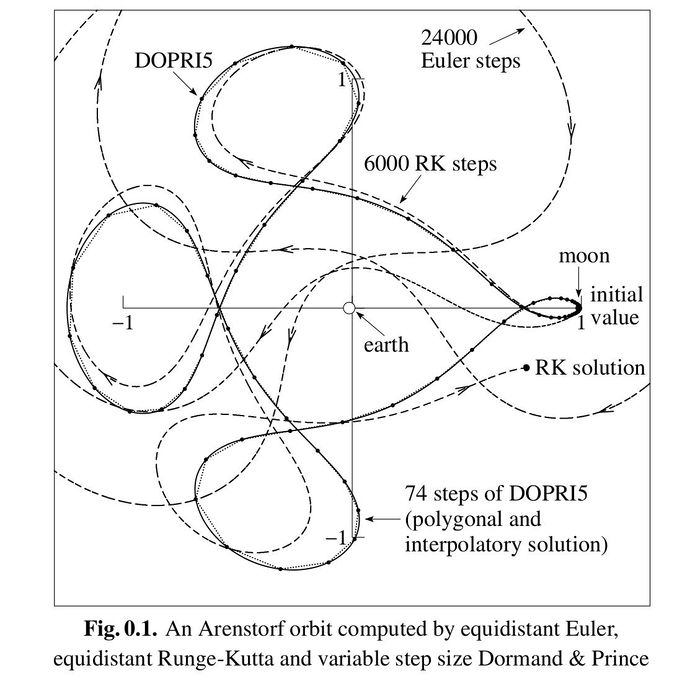
To demonstrate the state-of-the-art methods for computing the motion of bodies in Celestial Mechanics, poliastro, an astrodynamics software developer, has shared this beautiful plot of several numerical methods for the Restricted Three Body Problem when applied to the Sun-Earth-Moon system, taken from Harier et al. Solving Ordinary Differential Equations I.
The use of high order Runge-Kutta methods is pervasive in Celestial Mechanics.
—poliastro
|
When the numerical Three Body Problem solutions in Celestial Mechanics are applied to model the movement of the Moon in the Earth-Moon-Sun system we get the following:
Arenstorf orbits are the knotted closed trajectories which are the result of Restricted Three Body Problem solutions.
The Zeroth Step
In 2017, by testing out many possible orbits to find stable ones, a supercomputer found over one thousand new numerical solutions to the Three Body Problem.
Infamous three-body problem has over a thousand new solutions
The new solutions were found when researchers at Shanghai Jiaotong University in China tested 16 million different orbits using a supercomputer.
—newscientist
|
Perhaps the most important application of the three-body problem is in astronomy, for helping researchers figure out how three stars, a star with a planet that has a moon, or any other set of three celestial objects can maintain a stable orbit.
But these new orbits rely on conditions that are somewhere between unlikely and impossible for a real system to satisfy. In all of them, for example, two of the three bodies have exactly the same mass and they all remain in the same plane.
—newscientist
|
Knot-like paths
In addition, the researchers did not test the orbits’ stability. It’s possible that the tiniest disturbance in space or rounding error in the equations could rip the objects away from one another.
“These orbits have nothing to do with astronomy, but you’re solving these equations and you’re getting something beautiful,” says Vanderbei.
Aside from giving us a thousand pretty pictures of knot-like orbital paths, the new three-body solutions also mark a starting point for finding even more possible orbits, and eventually figuring out the whole range of winding paths that three objects can follow around one another.
“This is kind of the zeroth step. Then the question becomes, how is the space of all possible positions and velocities filled up by solutions?” says Richard Montgomery at the University of California, Santa Cruz. “These simple orbits are kind of like a skeleton to build the whole system up from.”
—newscientist
|
As plainly stated, the stable orbits that can be found have nothing that looks like heliocentric astronomy. The system, at its very basic level, is unable to be created.
The "thousands of stable solutions" are scenarios where the bodies have the same mass or where one of the bodies is mass-less. All of these scenarios are incredibly sensitive, and none represent anything that looks like a heliocentric system. They are crazy loopy orbits, based on situations that would not happen in nature, and which fall apart with the slightest touch.
Chaos Theory: A Demo
The available solutions to the Three Body Problem, beyond being unlike anything seen in Heliocentric Theory, are so sensitive that the slightest change or imperfection will tear the entire system apart. As a very illustrative demonstration, take a look at this online Three Body Problem simulator that uses the simplest possible figure eight pattern, which requires three identical bodies of equal mass that move at very specific momentum and distance in relation to each other.
Demo: Figure-Eight Three Body Problem
Adjust the slider values in the upper left to something very slight to find what happens. What you will see is a demonstration of Chaos Theory. Any slight modification to the system creates a chain reaction of random chaos.
This is precisely the issue of modeling the Heliocentric System, and why its fundamental system cannot exist. Only very specific and very sensitive configurations may exist. The slightest deviation, such as with a system with unequal masses, or the minute influence from a gravitating body external to the system, will cause the entire system to fly apart! The reader is invited to decide for his or her own self whether those those scenarios would happen in nature as described by popular theory.
Official Explanation: Divine Intervention
The reader may question how Issac Newton, the authority who "brought the laws of physics to the solar system,"1 answered this issue. His answer is described in the book The KAM Story by professor H. Scott Dumas, where we read the following:
At the beginning of the 18th century, Newton famously wrote that the solar system needed occasional divine intervention (presumably a nudge here and there from the hand of God) in order to remain stable.11 This was interpreted to mean that Newton believed his mathematical model of the solar system—the n body problem—did not have stable solutions. Thus was the gauntlet laid down, and a proof of the stability of the n body problem became one of the great mathematical challenges of the age.
11Newton's remarks about divine intervention appear in Query 23 of the 1706 (Latin) edition of Opticks, which became Query 31 of the 1717 (2nd Edition) edition see Quote Q[New] in Appendix E). Similar 'theological' remarks are found in scholia of the 2nd and 3rd editions of Principia, and in at least one of Newton's letters. In a 1715 letter to Caroline, Princess of Wales, Leibniz observed sarcastically that Newton had not only cast the Creator as a clock-maker, and a faulty one, but now as a clock-repairman (see [Klo73], Part XXXIV, pp. 54-55).
—The KAM Story
|
1The University of California San Diego credits Newton as providing the laws of physics for the Solar System:
Then came Isaac Newton (1642-1727) who brought the laws of physics to the solar system. Isaac Newton explained why the planets move the way they do, by applying his laws of motion, and the force of gravitation between any two bodies, letting the force decrease with the square of the distance between the two bodies.
—UC San Diego
|
.
Conclusion
As we have read, it is well admitted that Celestial Mechanics is not, and cannot, be used for the prediction of bodies in the solar system. Nor can it even create a heliocentric orbit of its simplest elements. The idea that it is used with success in astronomy software, and that astronomy literature is able to predict bodies into the future is, to say the least, misinformed. Celestial prediction software such as Stellarium are not "Round Earth" or "Heliocentric" prediction tools.
The n-body problem is the foundation of the entire field of Celestial Mechanics and the massive attempt to show the possibility of Heliocentric orbits. The efforts of hundreds of mathematicians and astronomers over hundreds of years, from the early beginnings, have failed again and again to predict or simulate motion in the system. After so much time, with such great effort by the greatest minds of history to make this system work, Celestial Mechanics is still at step zero. It is an embarrassing stain on the whole of astronomy, mathematics, and classical mechanics. The above works identify the inability to predict or create as "chaos," and from this it takes little effort to transition into a questioning of the system and the science itself.
Not only can astronomy not predict, not only can it not simulate a basic heliocentric system such as a stable earth-moon system rotating around a sun, hundreds of years of research into the matter as one of the greatest unsolved issues in science has thus-far shown that the heliocentric system cannot exist at all.
This Emerald City of Superior Predictive Ability that is used to showcase and prove the factual reality of the Round Earth System in its splendor and beauty, is revealed to be little more than a facade. The predictive power of the Round Earth System is not beautiful at all. When the Wizard's mandatorily worn spectacles, which supposedly protects inhabitants and visitors from the blinding light and brilliance, are removed from the eyes, the city is seen to be no more green than any other city. The proprietor behind the curtain is handing out phony diplomas from his palace, and we are asked to pay no attention.
The following comment left on our forum on this topic is succinct:
This point is a very powerful objection to astronomical theory in general, as opposed to observations. If all the movements of celestial bodies are simply predicted by tables based on observations of patterns, and if there is no simpler model available that explains these patterns, then there is no theory at all. We only have the observations.
This certainly deserves a separate thread. The whole project of science is based on taking complex observations, then elucidating a simpler theory or model that explains the observations. This is crucial.
—edby
|
Perhaps that is true [of the NOAA Solar Calculator], but if it were true of all astronomy, it would invalidate the entire project of Western science.
—edby
|
Indeed.
From the failure of theory to meet reality, we are reminded of the following words by Samuel Birley Rowbotham:
None can doubt that by making special experiments, and collecting manifest and undeniable facts, arranging them in logical order, and observing what is naturally and fairly deducible therefrom, the result must be more consistent and satisfactory than the contrary method of framing a theory or system--assuming the existence and operation of causes of which there is no direct and practical evidence, and which is only claimed to be "admitted for the sake of argument," and for the purpose of giving an apparent and plausible, but not necessarily truthful explanation of phenomena. All theories are of this character. "Supposing, instead of inquiring, imagining systems instead of learning from observation and experience the true constitution of things. Speculative men, by the force of genius may invent systems that will perhaps be greatly admired for a time; these, however, are phantoms which the force of truth will sooner or later dispel; and while we are pleased with the deceit, true philosophy with all the arts and improvements that depend upon it, suffers. The real state of things escapes our observation; or, if it presents itself to us, we are apt either to reject it wholly as fiction, or, by new efforts of a vain ingenuity to interweave it with our own conceits, and labour to make it tally with our favourite schemes. Thus, by blending together parts so ill-suited, the whole comes forth an absurd composition of truth and error. * * * These have not done near so much harm as that pride and ambition which has led philosophers to think it beneath them to offer anything less to the world than a complete and finished system of Nature; and, in order to obtain this at once, to take the liberty of inventing certain principles and hypotheses from which they pretend to explain all her mysteries."
"Theories are things of uncertain mode. They depend, in a great measure, upon the humour and caprice of an age, which is sometimes in love with one, and sometimes with another."
The system of Copernicus was admitted by its author to be merely an assumption, temporary and incapable of demonstration. The following are his words:--"It is not necessary that hypotheses should be true, or even probable; it is sufficient that they lead to results of calculation which agree with calculation. * * * Neither let anyone, so far as hypotheses are concerned, expect anything certain from astronomy, since that science can afford nothing of the kind, lest, in case he should adopt for truth, things feigned for another purpose, he should leave this science more foolish than he came. * * * The hypothesis of the terrestrial motion was nothing but an hypothesis, valuable only so far as it explained phenomena, and not considered with reference to absolute truth or falsehood."
The Newtonian and all other "views" and "systems" have the same general character as the "hypothesis of the terrestrial motion," framed by Copernicus. The foundations or premises are always unproved; no proof is ever attempted; the necessity for it is denied; it is considered sufficient that the assumptions seem to explain the phenomena selected. In this way it is that theory supplants theory, and system gives way to system, often in rapid succession, as one failure after another compels opinions to change. Until the practice of theorizing is universally relinquished, philosophy will continue to be looked upon by the bulk of mankind as a vain and mumbling pretension, antagonistic to the highest aspirations of humanity. Let there be adopted a true and practical free-thought method, with sequence as the only test of truth and consistency, and the philosopher may become the Priest of Science and the real benefactor of his species. "Honesty of thought is to look truth in the face, not in the side face, but in the full front; not merely to look at truth when found, but to seek it till found. There must be no tampering with conviction, no hedging or mental prevarication; no making 'the wish father to the thought;' no fearing to arrive at a particular result. To think honestly, then, is to think freely; freedom and honesty of thought are truly but interchangeable terms. For how can he think honestly, who dreads his being landed in this or that conclusion? Such as one has already predetermined in his heart how he shall think, and what he shall believe. Perfect truth, like perfect love, casteth out fear."
Let the method of simple inquiry--the "Zetetic" process be exclusively adopted--experiments tried and facts collected--not such only as corroborate an already existing state of mind, but of every kind and form bearing on the subject, before a conclusion is drawn, or a conviction affirmed.
"Nature speaks to us in a peculiar language; in the language of phenomena. She answers at all times the questions which are put to her; and such questions are experiments."
—Samuel Birley Rowbotham, Earth Not a Globe
|