Difference between revisions of "Round Earth Theory Curvature Calculations"
(Earth is a sphere) Tags: Blanking Undo |
PeteSvarrior (talk | contribs) m (Reverted edits by 107.167.244.83 (talk) to last revision by Tom Bishop) Tag: Rollback |
||
| Line 1: | Line 1: | ||
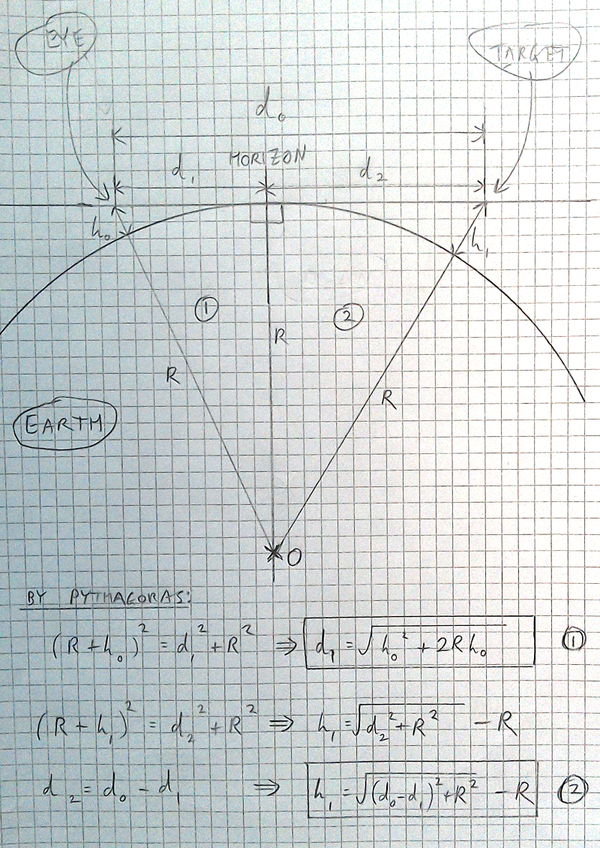
| + | =Manually Calculating the Amount Hidden by Curvature= | ||
| + | In order to calculate the amount that should be hidden we may use the Theory of Pythagoras. | ||
| + | |||
| + | [[File:Calc-method.png|600px]] | ||
| + | |||
| + | Diagram & Transformations Credit: dizzib | Theory Credit: Pythagoras | ||
| + | |||
| + | ==Important Equations== | ||
| + | |||
| + | To find the distance from the observer's eye to the horizon (d1) we first perform the following: | ||
| + | |||
| + | 1. d1 = sqrt(h0^2 + 2 * R * h0) | ||
| + | |||
| + | Next, we place d1 in the following equation to find the amount hidden below the horizon of the earth (h1): | ||
| + | |||
| + | 2. h1 = sqrt((d0 - d1)^2 + R^2) - R | ||
| + | |||
| + | ===Example 1: Sea Level=== | ||
| + | |||
| + | To calculate the amount hidden at sea level, over 6.23 miles, with an observer height of 32 inches, we convert to a like unit (e.g. km) and perform the following: | ||
| + | |||
| + | R = 6371 km<br> | ||
| + | h0 = 0.0008128 km (32 inches)<br> | ||
| + | d0 = 10.02621 km (6.23 miles)<br> | ||
| + | |||
| + | 1. d1 = sqrt(0.0008128^2 + 2×6371×0.0008128) = 3.21818<br> | ||
| + | 2. h1 = sqrt((10.02621 - 3.21818)^2 + 6371^2) - 6371 = 0.00363752 | ||
| + | |||
| + | 0.00363752 km converted to feet = 11.93412073491 feet hidden | ||
| + | |||
| + | ===Example 2: Lake Above Sea Level=== | ||
| + | |||
| + | To calculate the amount hidden across a lake with an altitude of 1368 meters above sea level, we make a slight adjustment to R and perform the following: | ||
| + | |||
| + | R = 6372.368 km (6371 km + 1368 m)<br> | ||
| + | h0 = 0.0008128 km (32 inches)<br> | ||
| + | d0 = 10.02621 km (6.23 miles)<br> | ||
| + | |||
| + | 1. d1 = sqrt(0.0008128^2 + 2×6372.368×0.0008128) = 3.21853<br> | ||
| + | 2. h1 = sqrt((10.02621 - 3.21853)^2 + 6372.368^2) - 6372.368 = 0.00363636 | ||
| + | |||
| + | 0.00363636 km converted to feet = 11.93031496063 feet hidden | ||
| + | |||
| + | =Online Calculator= | ||
| + | |||
| + | Based on the above, dizzib has provided an online calculator for computing the drop distance and the amount which should be hidden per observer height according to the curvature of the earth. | ||
| + | |||
| + | Link: https://dizzib.github.io/earth/curve-calc/ ([https://web.archive.org/web/20190618213453/https://dizzib.github.io/earth/curve-calc/?d0=30&h0=10&unit=imperial Archive]) | ||
| + | |||
| + | [[Category:Miscellaneous]] | ||
Latest revision as of 17:22, 15 October 2022
Manually Calculating the Amount Hidden by Curvature
In order to calculate the amount that should be hidden we may use the Theory of Pythagoras.
Diagram & Transformations Credit: dizzib | Theory Credit: Pythagoras
Important Equations
To find the distance from the observer's eye to the horizon (d1) we first perform the following:
1. d1 = sqrt(h0^2 + 2 * R * h0)
Next, we place d1 in the following equation to find the amount hidden below the horizon of the earth (h1):
2. h1 = sqrt((d0 - d1)^2 + R^2) - R
Example 1: Sea Level
To calculate the amount hidden at sea level, over 6.23 miles, with an observer height of 32 inches, we convert to a like unit (e.g. km) and perform the following:
R = 6371 km
h0 = 0.0008128 km (32 inches)
d0 = 10.02621 km (6.23 miles)
1. d1 = sqrt(0.0008128^2 + 2×6371×0.0008128) = 3.21818
2. h1 = sqrt((10.02621 - 3.21818)^2 + 6371^2) - 6371 = 0.00363752
0.00363752 km converted to feet = 11.93412073491 feet hidden
Example 2: Lake Above Sea Level
To calculate the amount hidden across a lake with an altitude of 1368 meters above sea level, we make a slight adjustment to R and perform the following:
R = 6372.368 km (6371 km + 1368 m)
h0 = 0.0008128 km (32 inches)
d0 = 10.02621 km (6.23 miles)
1. d1 = sqrt(0.0008128^2 + 2×6372.368×0.0008128) = 3.21853
2. h1 = sqrt((10.02621 - 3.21853)^2 + 6372.368^2) - 6372.368 = 0.00363636
0.00363636 km converted to feet = 11.93031496063 feet hidden
Online Calculator
Based on the above, dizzib has provided an online calculator for computing the drop distance and the amount which should be hidden per observer height according to the curvature of the earth.