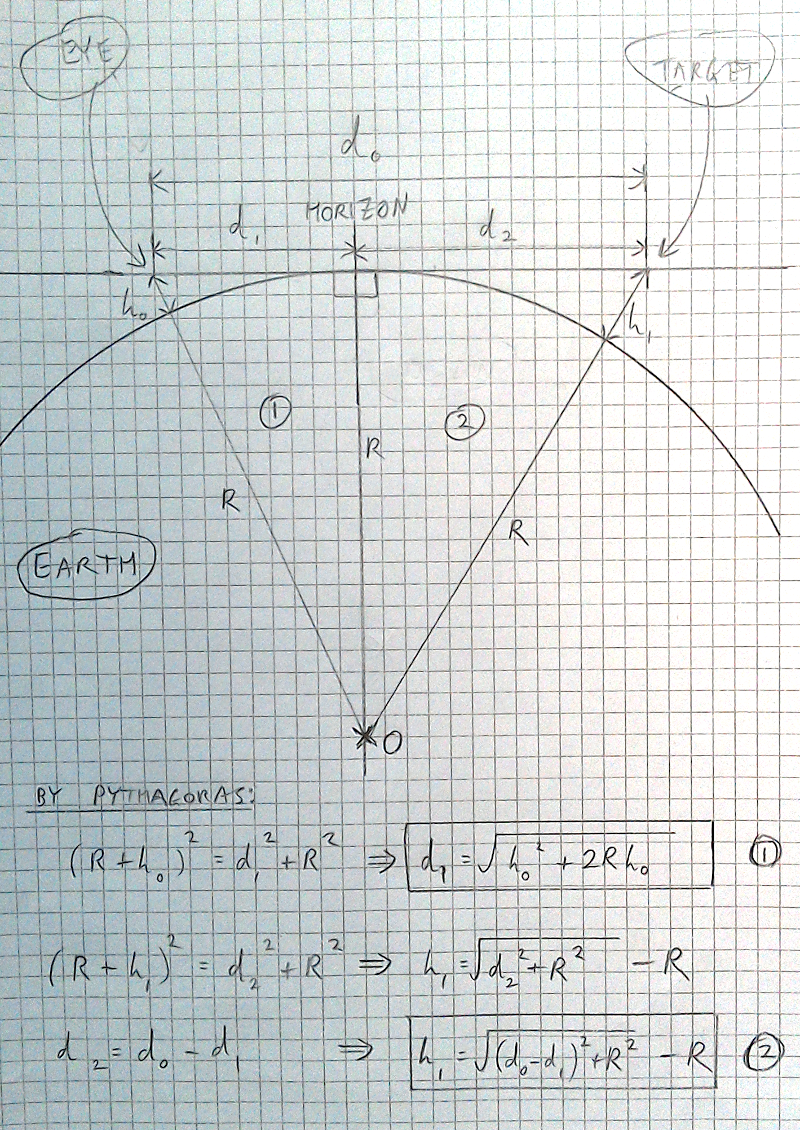
Round Earth Theory Curvature Calculations
Manually Calculating the Amount Hidden by Curvature
In order to calculate the amount hidden we may use the Theory of Pythagoras.
Illustration Credit: dizzib | Theory Credit: Pythagoras
Important Equations
To find the distance from the observer's eye to the horizon we first perform the following:
1. d1 = sqrt(h0^2 + 2 * R * h0)
Next, we place that in the following equation to get the amount hidden behind the alleged curvature of the earth:
2. h1 = sqrt((d0 - d1)^2 + R^2) - R
Example 1: Sea Level
To calculate the amount hidden at sea level, over 6.23 miles, with an observer height of 32 inches, we convert to a like unit (ie. km) and perform the following:
R = 6371 km
h0 = 0.0008128 km (32 inches)
d0 = 10.02621 km (6.23 miles)
1. d1 = sqrt(0.0008128^2 + 2×6371×0.0008128) = 3.21818
2. h1 = sqrt((10.02621 - 3.21818)^2 + 6371^2) - 6371 = 0.00363752
0.00363752 km converted to feet = 11.93412073491 feet hidden
Example 2: Lake Above Sea Level
To calculate the amount hidden by a lake with an altitude 1368 meters, we make a slight adjustment to R and perform the following:
R = 6372.368 km (6371 km + 1368 m)
h0 = 0.0008128 km (32 inches)
d0 = 10.02621 km (6.23 miles)
1. d1 = sqrt(0.0008128^2 + 2×6372.368×0.0008128) = 3.21853
2. h1 = sqrt((10.02621 - 3.21853)^2 + 6372.368^2) - 6372.368 = 0.00363636
0.00363636 km converted to feet = 11.93031496063 feet hidden