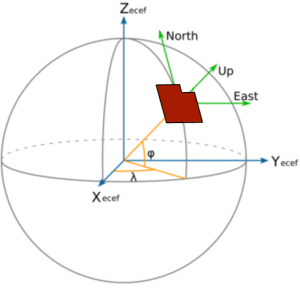
WGS84
Definitions
Geographic Coordinate System
A Geographic Coordinate System is a spherical coordinate system which uses longitude and latitude.
From What are geographic coordinate systems? by ArcGIS:
“ A geographic coordinate system (GCS) uses a three-dimensional spherical surface to define locations on the earth. A GCS is often incorrectly called a datum, but a datum is only one part of a GCS. A GCS includes an angular unit of measure, a prime meridian, and a datum (based on a spheroid). ”
The World Geodetic System 1984 (WGS84) is an example of a Geographic Coordinate System.
Projected Coordinate System
A Projected Coordinate System is a planar coordinate system.
From What are Projected Coordinate Systems? by ArcGIS:
“ A projected coordinate system is defined on a flat, two-dimensional surface. Unlike a geographic coordinate system, a projected coordinate system has constant lengths, angles, and areas across the two dimensions. ”
The State Plane Coordinate System (SPCS) is an example of a Projected Coordinate System
Datums
A Datum is an anchor point which ties two systems (geographic and projected) coordinate systems together.
From Datums by ArcGIS we read:
“ While a spheroid approximates the shape of the earth, a datum defines the position of the spheroid relative to the center of the earth. A datum provides a frame of reference for measuring locations on the surface of the earth. It defines the origin and orientation of latitude and longitude lines. ”
The North American Datum 1983 (NAD83) is an example of a datum.
State Plane Coordinate Systems and NAD83
State Plane Coordinate Systems are widely used for geographic data, and are based on a flat earth 'plane surveying' methods with simple XY coordinates:
https://en.wikipedia.org/wiki/State_Plane_Coordinate_System
“ The State Plane Coordinate System (SPS or SPCS) is a set of 124 geographic zones or coordinate systems designed for specific regions of the United States. Each state contains one or more state plane zones, the boundaries of which usually follow county lines. There are 110 zones in the contiguous US, with 10 more in Alaska, 5 in Hawaii, and one for Puerto Rico and US Virgin Islands. The system is widely used for geographic data by state and local governments. Its popularity is due to at least two factors. First, it uses a simple Cartesian coordinate system to specify locations rather than a more complex spherical coordinate system (the geographic coordinate system of latitude and longitude). By using the Cartesian coordinate system's simple XY coordinates, "plane surveying" methods can be used, speeding up and simplifying calculations. ”
Lower down in that article we read that the State Plane Coordinate Systems are associated with the North American Datum of 1983:
“ Originally, the state plane coordinate systems were based on the North American Datum of 1927 (NAD27). Later, the more accurate North American Datum of 1983 (NAD83) became the standard (a geodetic datum is the way a coordinate system is linked to the physical Earth). More recently there has been an effort to increase the accuracy of the NAD83 datum using technology that was not available in 1983. ”
The United States Government echoes the same association:
https://catalog.data.gov/dataset/united-states-stateplane-zones-nad83
“ United States Stateplane Zones - NAD83 Metadata Updated: August 11, 2016
U.S. State Plane Zones (NAD 1983) represents the State Plane Coordinate System (SPCS) Zones for the 1983 North American Datum within United States. ”
The Earth is Not Round!
The Earth is Not Round! Utah, NAD83 and WebMercator Projections
By the Utah Automated Geographic Reference Center
Anchor Point Datum
It has been asked what the ellipsoid and center-of-earth anchor point that is associated with the NAD83 is referring to. If the NAD83 is composed of state plane maps with a flat XY coordinate system, why is there a reference to involvement of a globe model?
From the 'The Earth is Not Round!' article we read:
“ The UTM NAD83 projection uses the GRS80 ellipsoid and a center-of-the-earth anchor point as its datum ”
The ellipsoid and anchor point associated with NASD84 is necessary to interconnect with other spherical models, in order to connect correctly at the correct location and interchange data.
First it talks about the spherical model:
“ Geographic coordinates use latitude and longitude values to define positions on the 3D surface of the earth, which is of course, best modeled as an ellipsoid, not a sphere. The ellipsoid and its accompanying anchor point that ties it in to the real world, are known collectively as the WGS84 datum. ”
Note "real world."
Then it talks about the flat model:
“ UTM NAD83 is a projected coordinate system that represents physical locations abstracted to a flat, cartesian coordinate system. The UTM NAD83 projection uses the GRS80 ellipsoid and a center-of-the-earth anchor point as its datum ”
The passage is speaking of an anchor point to connect the two types of systems together.
The accompanying image is the flat map with anchor point:
WGS84 Requires Flat Maps
WGS84 relies on flat projections to give out accurate data.
https://www.gpsworld.com/data-collection-of-wgs-84-information-or-is-it/
“ In the meantime, here are a few of the main differences between WGS 84 and NAD83:
The coordinate system for WGS 84 is geographic, and the NAD83 system is projected. ”
As we will recall from the definitions section, a geographic coordinate system is spherical and a projected coordinate system is flat. NAD83 provides a flat coordinate system.
https://www.gpsworld.com/data-collection-of-wgs-84-information-or-is-it/
“ WGS84 doesn't define a projection, so it's up to the GIS software to decide which projection to use for displaying the data on the screen (unless you manually pick a projection, of course). ”
Take a look at the list of projections for the ARCGIS software:
ArcGIS 10.7.0 and ArcGIS Pro 2.3 Geographic and Vertical Transformation Tables
These are the world-wide transformation tables used with ARCGIS, of which NAD83 is one of them. These are all flat coordinate systems. It is taking data from flat systems, because as the "Earth Not Round!" article says, these flat systems that are more accurate and give out more accurate figures.
Spherical Coordinates Projected To a Plane
“ The State Plane Coordinate System was established to provide a means for transferring the geodetic positions of monumented points to plane coordinates that would permit the use of these monuments in plane surveying over relatively large areas without introducing significant error.
A plane-rectangular coordinate system is by definition a flat surface. Geodetic positions on the curved surface of the earth must be “projected” to their corresponding plane coordinate positions. Projecting the curved surface onto a plane requires some form of deformation. Imagine the stretching and tearing necessary to flatten a piece of orange peel. In California the Lambert Conformal map projection is used to transform the geodetic positions of latitude and longitude into the y (Northing) and x (Easting) coordinates of the CCS83. ”
We read that the geographic (spherical) coordinates are projected to the plane coordinates. Not the other way around.
West Virginia GIS Technical Center
“ Geographic Coordinate System (GCS): An unprojected coordinate system that uses latitude and longitude to define the locations of points on a sphere or spheroid. The use of longitude and latitude is encouraged for general reference and distribution of national framework data because it provides a seamless coordinate system for most of the United States. Geographic coordinates can be readily projected onto a planar coordinate system to display data properly or measure distances accurately. The Geographic Coordinate System is the recommended coordinate system for unprojected GIS data sets that cover the entire geographic extent of West Virginia. ”
We read that the geographic (round earth) coordinates can be projected onto a planar (flat earth) coordinate system to accurately display distances.
The reader should ponder how spherical coordinates projected onto a planar coordinate system could display data and distances accurately if the earth is a globe. Why should these systems require that? Are maps with spherical coordinates are not possible?
If the earth is a globe, the opposite should be true. Projecting spherical coordinates onto a plane should make data and distances more inaccurate. Not accurate.
Classified Coordinate Transformations
Of interest, some coordinate transformations are not publicly known.
“ Why are there so many transformations?
Between any two geographic coordinate systems, there may be zero, one, or many transformations. Some geographic coordinate systems do not have any publicly known transformations because that information is considered to have strategic importance to a government or company. ”
Flat Maps as Standard
We find several sources which describe that flat maps are the standard in GIS work.
From https://www.e-education.psu.edu/geog862/book/export/html/1644 we read:
“ Welcome to Lesson Six of this GPS course. And this time, we'll be talking about two coordinate systems. And I have a little bit of discussion concerning heights. We've touched on that a little bit. Now these coordinate systems that we're going to discuss are plane coordinate systems based upon the fiction that the earth is flat, which, of course, immediately introduces distortion. However, much of GIS work—and GPS work as well—is done based upon this presumption. ”
Another comment: https://www.pobonline.com/articles/86585-geodetic-surveying-made-plain
“ A decade or two ago, I was the instructor for some introductory surveying courses at a community college. In the first class we would define “plane surveying” as surveying that did not take into consideration the curvature of earth, and “geodetic surveying” as that which did. That was about the only time the two categories received anywhere near equal attention. Oh, we would point out (still in that first lecture) some of the real-world evidence of a non-flat earth, such as the fact that the length of an 11.5-mile arc on the earth's surface is only five hundredths of a foot longer than its subtended chord, or that the sum of the angles in a spherical triangle on the earth’s surface having an area of 75 square miles is only one second greater than the angle sum of the same size plane triangle. (Even today I get a kick out of those dramatic tidbits. I’m sure a real geodesist would roll his or her eyes at such trivia!) But those examples were used as reasons for not focusing—no, for not mentioning—geodetic concepts for the rest of the semester. We would end the ten-minute token nod to geodetic surveying with the tongue-in-cheek remark, “Therefore, for this class, we will respect the time-honored principle handed down through the ages—that the earth is flat.” And, truth be known, that’s probably not a bad narrowing of a dauntingly broad subject.
But more than narrowing, it was simply that few rank-and-file surveyors in private practice ever had occasion to use geodetic concepts in their daily work. Even when we dutifully enrolled in the occasional State Plane Coordinate seminar, the principles quickly faded from memory from lack of use. If a surveyor from the general population had ever even heard of the geoid and its relationship to the ellipsoid, and where mean sea level fit into the picture, hearing about it was as far it went. ”
We see that flat maps are the standard.