High Altitude Horizon Dip
High Altitude Horizon Dip
JTolan has published an interesting series of videos in which a camera with an infrared filter is taken up on a plane to an altitude of 33,000 feet, where he is able to see much further than the Round Earth Theory should allow. Mountains and other bodies which should be below the horizon are instead above the horizon and visible.
In his Infrared Flight over Gulf of Mexico video an analysis is performed showing that, although he can see various bodies much further than should be seen, the horizon is not where it should be on either a Flat Earth or a Round Earth model. According to a planar prediction the horizon should be at 0 degrees eye level. According to a Round Earth prediction the horizon should be at 3.2 degrees below eye level. Yet the horizon matches neither model.
Infrared Flight over Gulf of Mexico HD1080 (16:00 mark)
"Globe Horizon" is the geometric prediction for the globe. "Globe Horizon (4/3R)" is the globe earth + standard refraction theory.
Since the height of the horizon matches neither model, the above analysis may suggest that either:
- The earth is round and massive downwards bending of light is occurring
- The earth is flat and massive upwards bending of light is occurring
- Light is traveling in straight lines and the earth is something else (ie. a globe much larger than claimed, or other model)
Under a flat earth model it can be interpreted as evidence that light is bending upwards on a large scale.
Gulf of Mexico Analysis
As verification for the author's procedure and methods, see the following:
Red Ball Example
It is possible to determine where eye level is in an image if one has knowledge of his or her position and the positions of distant bodies or structures.
As an example, if your eye is at an altitude of 5 feet, 6 inches, and there is an object, say a red ball on a post, 500 feet away from you, which is also at altitude of 5 feet, 6 inches, then the position of that ball to you will be parallel on the horizontal. The path to that object will be at your eye level.
Instead, lets say that the red ball is 500 feet away from you and 2 feet in altitude above the surface. In order to find its position in degrees below eye level we can use the knowledge that there is a gap of 3 feet, 6 inches; a space which represents where the hypothetical eye level ball would be.
Perform the calculations for angular diameter of that space manually or find an angular diameter calculator. At 500 feet, 3.5 feet (3 feet, 6 inches) makes up 0.401 degrees of space. Therefore a ball that is 500 feet away from you and 2 feet in altitude is 0.401 degrees below eye level.
JTolan is using the above method, but adapted to the distances involved.
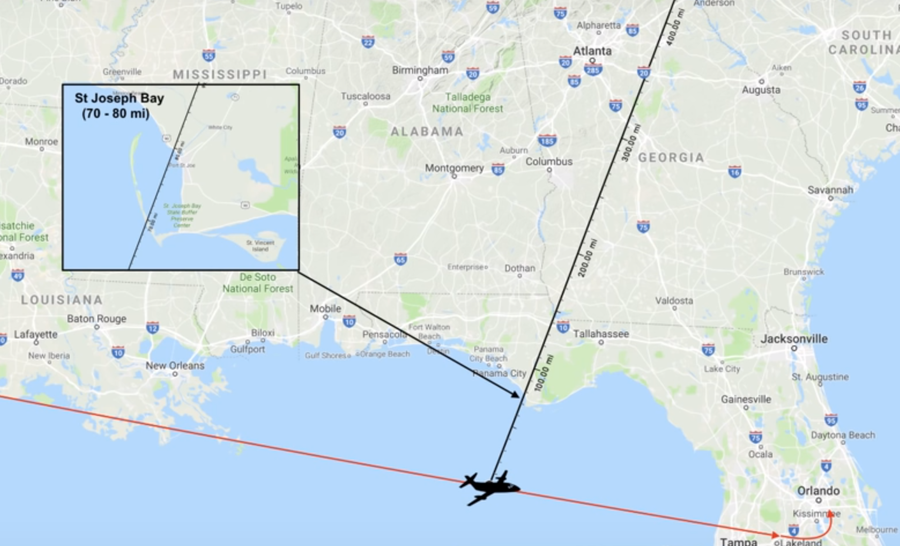
Location
According to the author, his GPS and flight path shows that he is 33,000 feet in altitude and at a location 71 miles from the start of Joseph Bay, closest to the observer, and 79 miles from the far end of it, furthest from the observer.
Degrees Below Eye Level Scale
On a Flat Earth with traditional perspective theory and an eye level horizon, an object in the distance must be at an altitude of 33,000 feet in order to be at eye level with an observer who is at an altitude of 33,000 feet. We may compute the size of this space in degrees according to its distance from the observer with an angular diameter calculator.
https://rechneronline.de/sehwinkel/angular-diameter.php
Knowing that the St. Joseph Bay is 71 miles, or 374,880 feet, from the observer, we may use the above angular diameter calculator to find that a vertical span of 33,000 feet at a distance of 374,880 feet away makes up a space of 5.04 degrees from the observer's eye level down to where the observer would see the to the start (closest point to observer) of the bay. Therefore the start (observer near point) of St. Joseph Bay is 5.04 degrees below eye level. Performing the same for the end (observer furthest point) of St. Joseph Bay, 33,000 feet at a distance of 79 miles, or 417,120 feet, makes up a space of 4.531 degrees. Therefore the end of St. Joseph Bay is 4.531 degrees below eye level.
Subtracting the two, an equidistant scale may be created upon the image with the space between the start and end of St. Joseph Bay representing 0.509 degrees, which is consistent with JTolan's scale above.
Round Earth Horizon Dip
The horizon dip below the theoretical planar eye level for a geometric Round Earth and a Round Earth with 'Standard Refraction' may be verified with MetaBunk's Earth Curve Calculator. For a height value of 33,000 feet and a distance value of 300 miles away (distance value does not matter for the horizon dip calculation), the result is the following:
- With "Standard" refraction adjustment of 7/6 radius (4618.83 miles) [...]
- Refracted Horizon Dip = 2.979 Degrees, (0.0520 Radians)
- Geometric results (no refraction) [...]
- Geometric Horizon Dip = 3.217 Degrees, (0.0562 Radians)
Although the above calculator is using Standard Refraction 7/6R rather than the 4/3R which JTolan uses, the result is essentially the same. These values for the Round Earth 'horizon dip' are consistent with JTolan's scale above. The horizon should be 3.217 degrees below eye level with a Geometric Round Earth prediction and 2.979 degrees below eye level with a Standard Refraction Round Earth prediction.
Florida In Infrared
Another video Florida in Infrared shows a similar scale, with a similar horizon dip. On a plane over the Gulf of Mexico the author claims to have used an infrared filter to look over the state of Florida to the Atlantic Ocean beyond it; a much further distance than a geometric Round Earth horizon dip should allow.
Topics
Sunrise and Sunset - Sunrise and Sunset Main Page
- Electromagnetic Acceleration - EA Main Page
- Lunar Eclipse due to Electromagnetic Acceleration - The Lunar Eclipse occurs when the Moon moves beyond the Sun's light
- Celestial Sphere - The tails of comets, Aurora Borealis, Milky Way, and the path of the Moon and Sun are warped on a 'Celestial Sphere'
- Moon Tilt Illusion - Illuminated portion of the Moon does not point in the expected direction
- High Altitude Horizon Dip - Horizon dip at high altitudes may suggest a bending of light