Moon Tilt Illusion
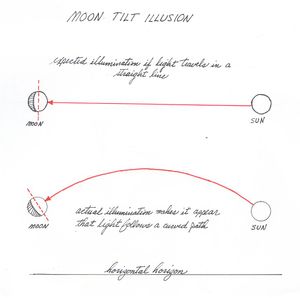
If the light travels in straight lines and the Sun illuminates the Moon then it is expected that the Moon's illuminated portion should always point at the Sun. The Moon Tilt Illusion is a phenomenon in which the lit portion of the Moon unexpectedly points away from the Sun. The phenomenon is most extreme for phases between Half Moon and Full Moon. The Moon Tilt Illusion even occurs after the Sun has set, a situation in which the the illuminated portion of the Moon is pointing upwards and away from the Earth while the Sun is below the horizon.
Some attribute this phenomenon to 'perspective', others suggest distortion in our visual field, while astronomers tell us that there is a 'celestial sphere' which the celestial bodies glide upon at different angles, and upon which straight lines become curved. We are given a series of analogies and explanations separate from, and incompatible with, the Round Earth Theory.
The Moon Tilt Illusion is geometric anomaly predicted by the Flat Earth Theory. Under the FET the Moon Tilt is directly predicted by Electromagnetic Acceleration (EA). The nature of EA results in the tilt of the Moon's phase away from and independent of the Sun's position and, for those who will accept the proof when furnished, acts as a vivid piece of evidence for the Flat Earth celestial model which is visible and accessible to all.
This page describes the Moon Tilt Illusion and the FE and RE explanations given for it. For the supplementary discussion on the String Experiment and Ball Experiment, which claim to be able to detect or replicate the presence of the illusion, see the page Moon Tilt Illusion Supplement
Description
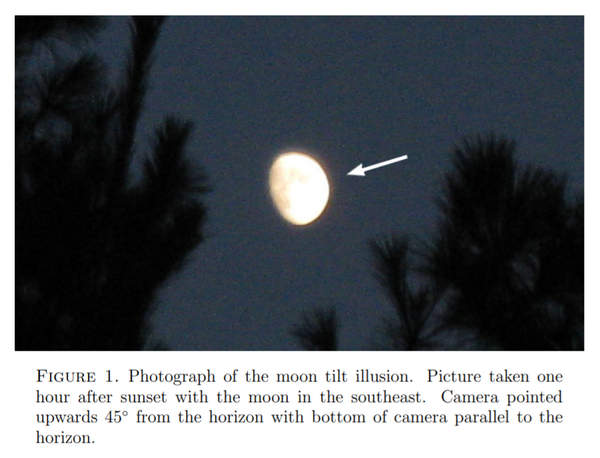
(Source)
Professor Myers at the University of Pennsylvania provides the following description:
http://www.upenn.edu/emeritus/essays/MyersMoon.html
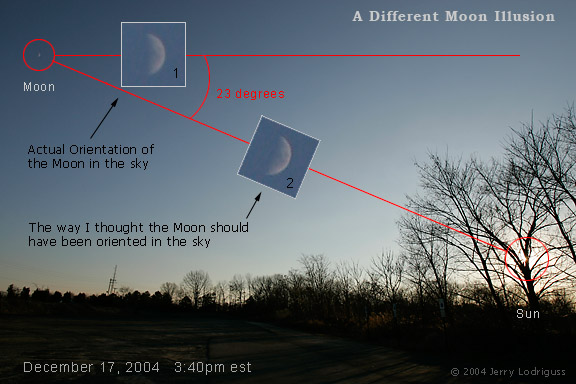
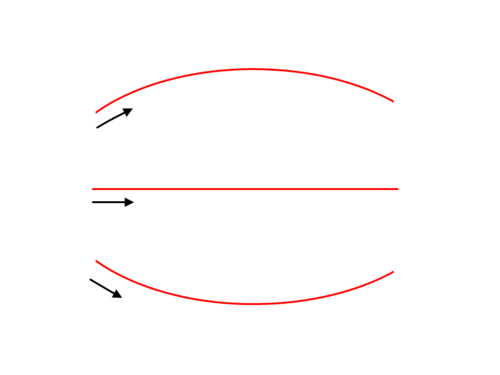
“ One evening several years ago, I took this picture of the misty glow of an almost full moon shining between pine trees in my backyard. The moon was beautifully illuminated and dominated the dark sky. Yet something was disturbing about the atmospheric night scene: the illumination of the moon seemed to be coming from the wrong direction! In this photograph of a waxing moon in the southern sky, its illumination appears to be coming from above to the right. But the sun---which had set an hour earlier---was already below the western horizon to the right when this photo was taken. If the sun is below the horizon, I thought, shouldn't its illumination of the moon appear to be coming from below the horizon? Intrigued, I made further observations when both the sun and the moon occupied the evening sky at the same time, and it certainly seemed that light rays from the sun would have to follow a curved path to shine on the moon at the observed angle. The sketch drawn below may help to explain the difference between what I expected to see and what I actually saw.
I asked everyone willing to listen if they were familiar with this illusion: why does a light ray from the sun to the moon appear to follow a curved path? No one had seen or heard of it. Several imaginative explanations were offered: "The light rays are bent by the earth's atmosphere." Or, "Gravitational lensing as predicted by Einstein's general theory of relativity is responsible." I was surprised not to find the illusion described in astronomy textbooks. I googled "moon illusion" but the articles were about an entirely different illusion: the apparent magnification of the full moon when it's close to the horizon.
Finally, help came from my daughter, who located published papers by googling "moon tilt illusion". The scientific explanation is based on the projection of a straight line onto the surface of a sphere. A simpler explanation was provided in a conversation with Benjamin Shen, Professor Emeritus of Astronomy at Penn, who said that light appears to follow a great circle route from the sun to the moon. That's why the moon's lit face appears to us not to face the sun squarely, regardless of whether the sun is above or below the horizon.
The moon tilt illusion is counter-intuitive and magical---look for it the next time you are under a night sky. ”
Moon Tilt Observational Diagram
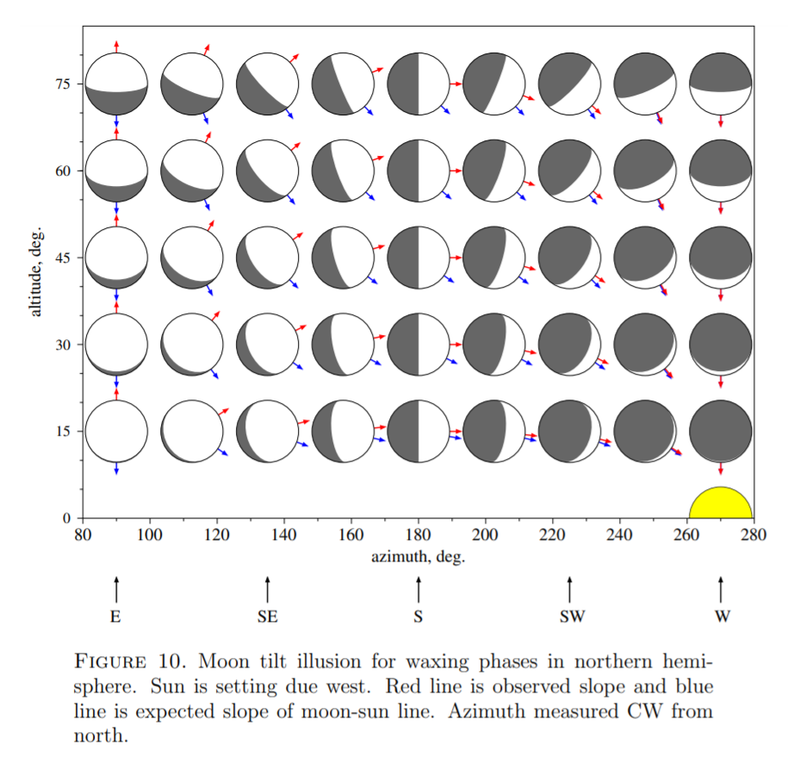
In a related paper from the same author titled The Moon Tilt Illusion (Archive), Professor Myers provides the following diagram of the observed tilt of the Moon and its displacement from the expected angle for waxing phases in the North:
Altitude is the elevation of the moon in the sky. Azimuth is the degrees clockwise from North. The diagram shows phases from full to new. At times the Moon is pointing towards the Sun, and at other times the Moon is pointing away from it. When opposite from the Sun, the Moon's tilt can be wildly displaced from its expected position.
Other Versions
From the source:
“ The most impressive illusion occurs at sunset when the gibbous moon is at high altitude in the southwest or at sunrise when the gibbous moon is at high altitude in the southeast (both cases for the northern hemisphere). ”
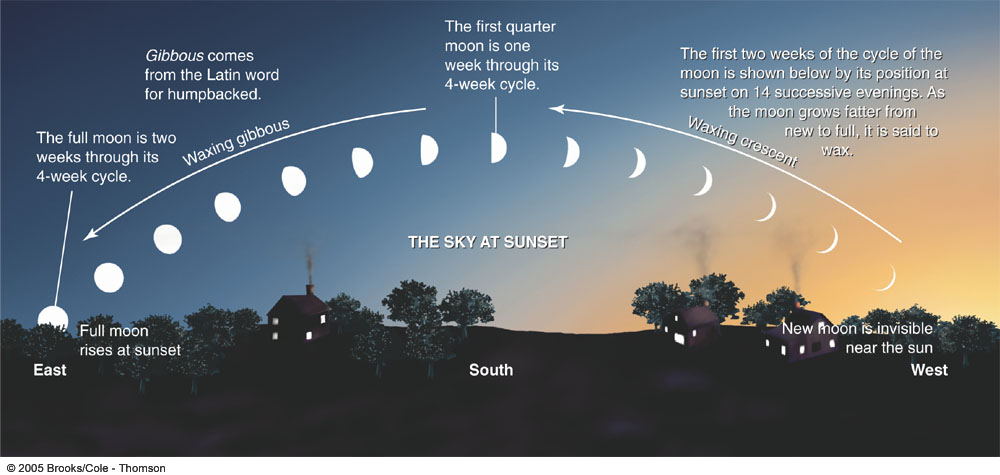
Lunar Phases at Sunset
Another depiction of the various orientations of the Moon in relation to the Sun at the time of sunset for waxing phases in the North may be found below:
(Source)
Other Versions
Sun and Moon Anomaly
From a Stack Exchange post on the Moon Tilt Illusion we find an observation (Archive):
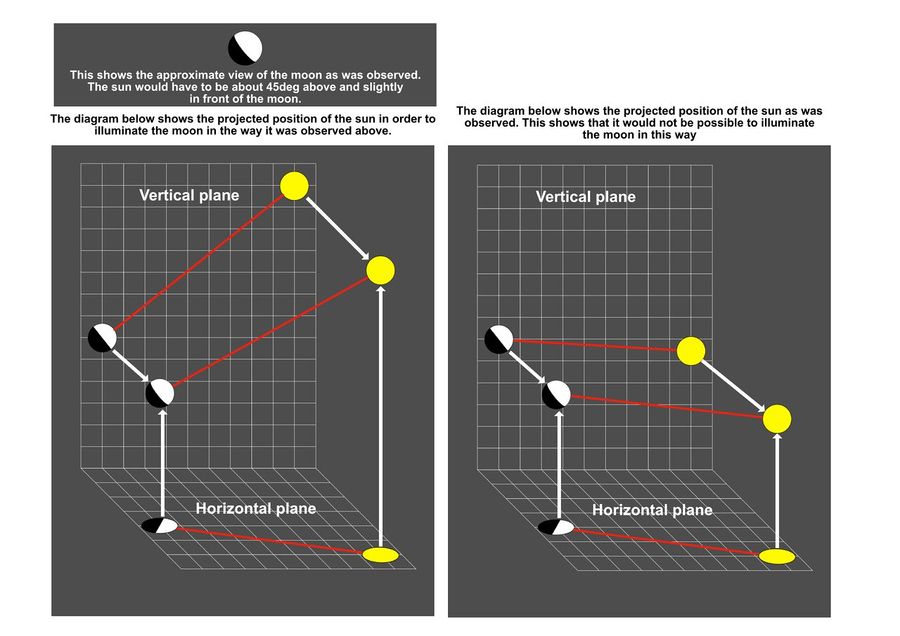
“ Below is a photo that my son took in Scotland showing the sun and moon at the same time. I immediately noticed this anomaly that the light illuminating the moon could not possibly come from the sun. I sent the photo to 4 University astronomy departments and only one responded and that was Cambridge University which is near where I live. The response came from the department librarian (not an astronomer) who said he had never heard of this before. He gave me two possible solutions, one was was from an engineer (not an astronomer) in which he got confused between perspective and light ray tracing and the other was referring to Einstein's theory of light bending by gravity. I check out Einstein and the effect was so small as to be almost immeasurable. ”
“ I have looked at the various 'complex' explanations for what to me is a very simple model. What need is there to introduce 'curved planes' and 'starry sky domes' all of which do not exist in reality? It is only referred to as an 'illusion' because observation doesn't fit the conventional model hence the complex explanations to try and make it work. The anomaly is acknowledged to exist with or without photos. Since everyone believes that the moon is illuminated by the sun then simple normal physics do not seem to work. Either the physics is wrong or the sun does not illuminate the moon. I realise that is a heavy statement!
Therefore I state once again:
- The sun and the moon are two objects (like a torch and a football) that are suspended in a 3 dimensional space and size should not matter.
- The moon/football are illuminated by the sun/torch and a perpendicular line or light ray can be drawn between them.
- It doesn't matter where in space you choose to view them, a perpendicular line or light ray can still be drawn between them.
This drawing explains my doubts: ”
“ I'm very surprised that some of you have never noticed it before hence the suggestion asking me to post a video. This is a very common occurrence and I have seen it many many times as I go for my morning walk at about 8.00am every morning. I have never thought of actually tabulating my observations. ”
Flat Earth Moon Tilt
It has been asked if there is an example of a celestial event that the Flat Earth Theory predicts which the Round Earth Theory does not. The Moon Tilt Illusion is one such example. While RET has difficulty explaining this anomaly, with university professors calling it "counter-intuitive and magical"[1], and multiple contradictory and geometrically questionable explanations are put forward in attempt to explain it, the phenomenon is directly predicted by the Flat Earth astronomical model. According to the theory of Electromagnetic Acceleration light curves upwards over very long distances, is the cause for the rising and setting of celestial bodies, and is responsible for dome-like effects involving curving celestial phenomena. When this scheme of upwardly bending light is applied to the orientation of the Moon it is seen that Electromagnetic Acceleration directly predicts the Moon Tilt Illusion.
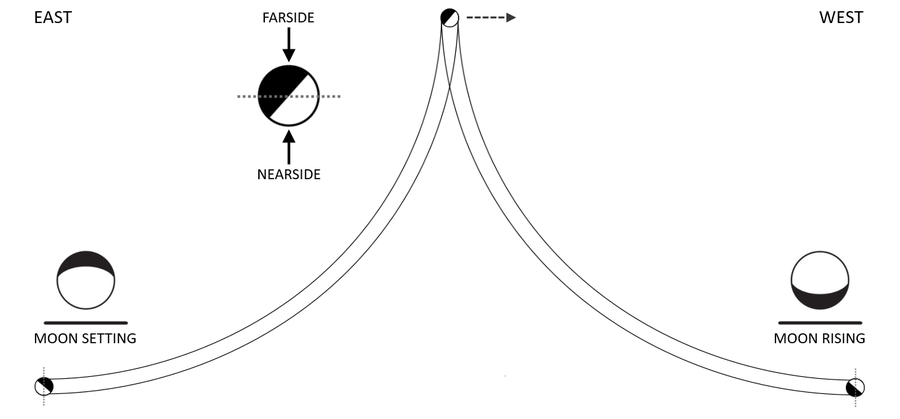
Moon Flipped
Due to EA the observer will always see the nearside (underside) of celestial bodies. As result, the orientation of the image on opposite sides will be upside-down. The illustration below shows the extremes of the Moon's rising and setting and the upside-down flipping of the Moon's image to observers positioned on opposite sides of the Moon.
An observer to the West of the Moon sees the phase pointed upwards away from the horizon, and an observer to the East of the Moon sees the phase pointed downwards towards the horizon.
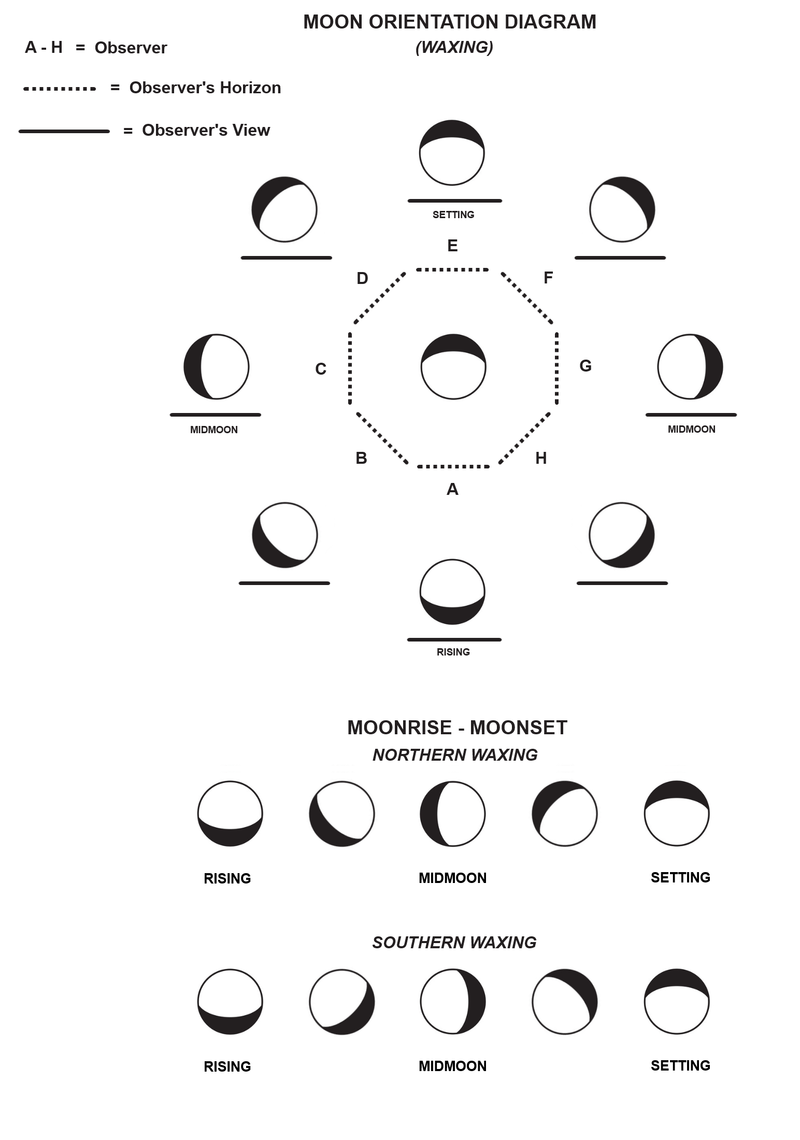
Moon Tilted
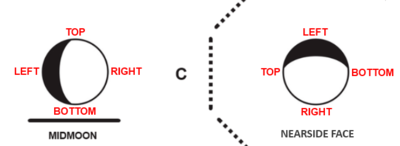
When viewing the Moon at various positions around it, it is seen that the Moon's phase tilts until it matches the opposite orientation. In the below illustration observers A - H are standing around the Moon, viewing it at various positions around it. The Moon over the solid horizon shows the observer's view. The central Moon illustration is the nearside (underside) of the Moon.
Notice that the views on opposite sides of each observer (A - H) are vertically flipped to each other like in the rising and setting side view diagram.
To simulate the view for each observer flip the central nearside face in relation to the observer's orientation around the Moon (positions A - H), so that the observer sees the furthest part of the Moon from his or her position at the closest to that observer's horizon. This represents each observer's view of the Moon.
For instance, Observer C at midmoon is looking to the right (Southward) at the Moon and from that position will see the darkened portion to the left of the Moon's image, with the furthest part of the Moon from Observer C's location at the bottom closest to that observer's horizon. The same may be applied for each observer, relative to their various positions around the Moon. Alternatively, one may take the vertically flipped rising phase for Observer A and rotate that image in 45 degree increments to match the positions of the Observers B - H around the Moon.
EA predicts that between rising and midmoon the Moon's phase will be pointed significantly away from the Earth, and independent of the Sun, angled in an upwards direction. At midmoon the illuminated portion of the Moon will be pointing at a right angle in the sky. Between midmoon and setting the phase will be pointing downwards towards the Earth. EA also predicts that the Moon's face will roll and rotate clockwise in the North and counter-clockwise in the South.
Comparison
Compare the EA Moon Tilt diagrams to the diagrams which were shown at the beginning of the page showing the Moon Tilt Illusion for the Waxing Phases in the North and South.
Round Earth Explanations
Perspective Explanation
An explanation of the Moon Tilt Illusion for the Round Earth Theory is given in the form of a perspective effect. It is possible to arrange yourself under an object so that it points upwards above your head. It is claimed that this is occurring with the Moon.
This is often demonstrated with a hallway. When standing in the middle of a hallway it is possible to see the edges of the ceiling angled in different directions by looking from the left to the right. From The Moon Tilt Illusion (Archive) we see:
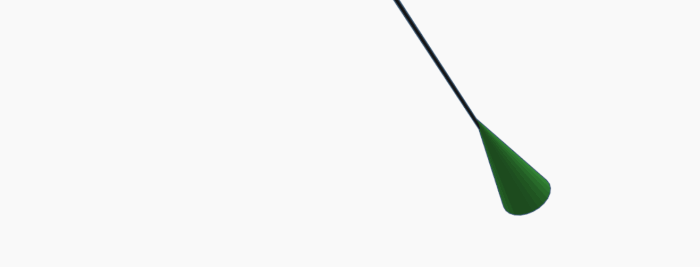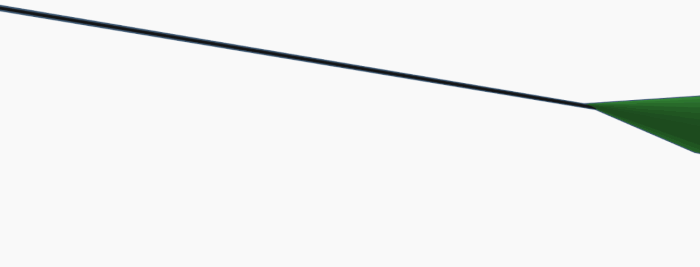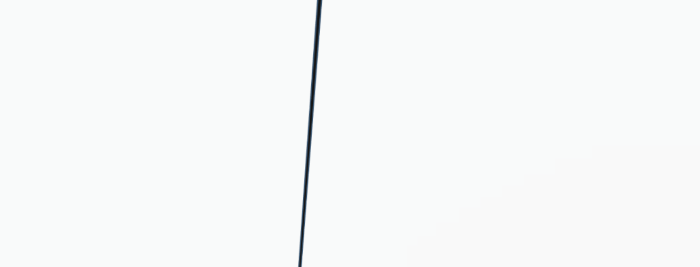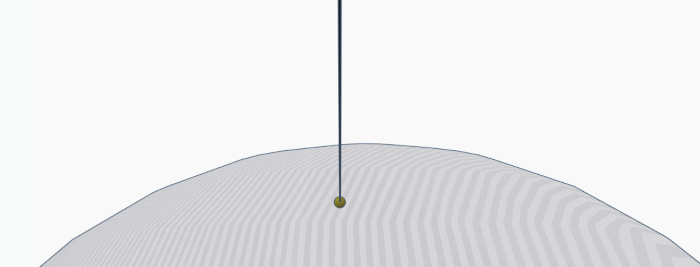
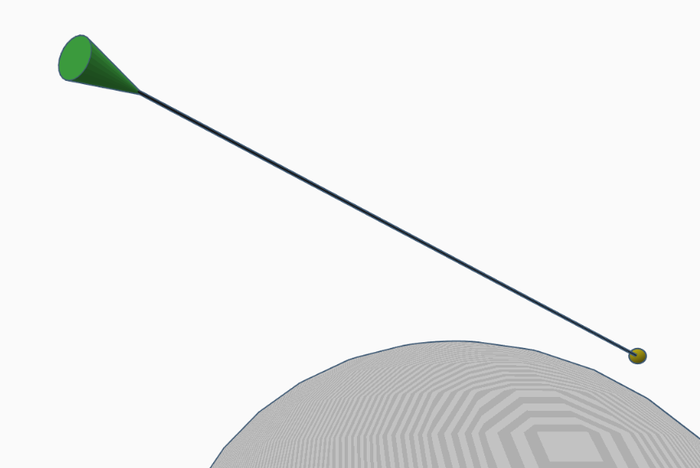
Using an example with a Green Cone (Moon) connected to a Sun on a straight line over a semi-transparent Earth, it is possible that the apparent direction of Green Cone is angled upwards when looking away from the Sun, and can apparently point in a straight line to a Sun below the horizon.
Scene zoomed out:
Two Object Problem
One issue with this explanation of 'perspective' is that if the observer is ever in a position to see both the Moon and Sun simultaneously, the illuminated portion of the Moon should point at the Sun. When moving the camera around the above scene, whenever the green cone and yellow ball are in the same field, the cone will always point at the ball along that straight line.
However, in contrast to this experimental determination of perspective, we find that with the Moon Tilt Illusion it is possible for an observer to see both the Moon and Sun simultaneously, misaligned to each other.
At https://www.astropix.com/html/observing/moonill.html (Archive) professional astrophotographer Jerry Lodriguss (bio) reports:
From the author:
“ Now, I have always under the impression that if you took the Moon's phase illumination angle it would draw a line straight back to the sun. But this sure wasn't what I thought I saw this day.
Obviously, it's an illusion that has something to do with a three-dimensional space being projected onto a two-dimensional plane in my eyeballs. Some people have tried to explain it as involving great circles, just as airplanes fly great circle routes to places on the opposite side of the globe. However they only do this because they can't fly a straight line through the Earth.
What I can't seem to get past is that the Sun and the Moon were in the same field together and I could view them both at the same time and that the light from the Sun is going in a straight line from the Sun to the Moon. It is not following a great circle. ”
In contradiction to this observation, it is seen that when the Moon and Sun are in the same field together and can be seen simultaneously the illuminated portion of the Moon should point at the Sun along a straight line.
String and Ball Experiments
It is sometimes argued that one can detect or replicate the illusion with a string or ball. This line of argumentation is addressed on the page Moon Tilt Illusion Supplement
Higher Sun Argument
It is also sometimes argued that the Moon would see the Sun from a higher position than the observer does, or that the Sun is illuminating from a higher position, as the rays of the Sun are parallel to the Earth-Moon system. This is a misinterpretation of the involved geometry; the Sun's rays are not exactly parallel to the RE Earth and Moon, and the Moon's illuminated area would point at the center of the Sun rather than any other point.
This is addressed at Moon Tilt Illusion Supplement - Higher Sun Argument
Visual Field Distortion
Another explanation for the Moon Tilt Illusion invokes distortion in the visual field. It is explained that we view the world with our visual sensory organs in a warped manner, to which our brain reprograms or ignores. A famous American artist named Todd Lockwood calls it 'curvilinear perspective' and explains it on the art education website Muddy Colors as so (Archive):
“ Our view of the universe is, in a real sense, like a fish-eye photo. Your field of view is a sphere, not a flat plane. But we fail to notice, in part because of our inability to see it all at once, and in part due to the psychology of perception derived from the fact that our visual organs and the cortex that interprets their data focus on the center … but also because we have been taught a formal way of interpreting the universe that insists on straight lines.
We tend to draw what we perceive in the center most area of our retina; our peripheral vision is an addendum. We rarely consider what’s going on outside our center of focus unless it looks like it might eat us. ”
Proponents of this idea generally claim that we view the world like a photograph from a fish-eye lens, but that the distortion is hidden from our conscious perception.
Noticable Distortion
An issue with this argument is that if there were warping in our vision then we should notice this effect with objects other than just the Moon. We should see bodies pointing upwards or downwards depending on where they were in our visual field.
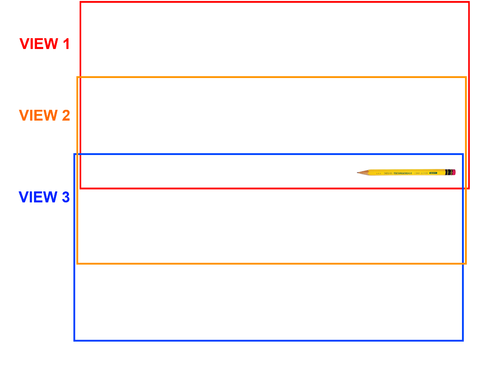
Pencil Warping
For example, if we had a horizontal pencil suspended in the air, changing its placement in our visual field should cause it to point upwards or downwards.
It is questionable why this effect apparently only applies to the Moon and is otherwise untestable.
Celestial Sphere
Yet another explanation for the Moon Tilt Illusion involves a "Celestial Sphere" in the sky, upon which straight lines become curved.
In the paper The Moon Tilt Illusion (Archive) by Adrea and Alan Myers, the following is stated:
“ The moon tilt illusion is not described in astronomy textbooks because astronomers know that straight lines in object space become great circles on the celestial sphere. Minnaert [5] gives only a passing reference: “...the line connecting the horns of the moon, between its first quarter and full moon, for instance, does not appear to be at all perpendicular to the direction from sun to moon; we apparently think of this direction as being a curved line. Fix this direction by stretching a piece of string taut in front of your eye; however unlikely it may have seemed to you at first you will now perceive that the condition of perpendicularity is satisfied”. An article by Sch¨olkopf [8] documents the illusion in an experiment involving 14 subjects by having them indicate their expectation of how the moon’s illumination should be oriented with respect to the position of the (visible) sun. He reports that an average discrepancy of 12◦ is perceived by the subjects between the observable versus expected orientation of the moon’s bright limb. Schott’s website entitled “ ‘Falsche’ Mondneigung” (‘False’ Moontilt) [9] is devoted to the moon tilt illusion, and features illustrations and useful links. Schott correctly proposes to quantify the effect by comparing the observed tilt angle with the angle from horizontal of the line connecting the moon and sun, but an error in geometry leads to an incorrect expression for the expected tilt. A paper by Glaeser and Schott [2], approaching the phenomenon via the principles of photography, show that the magnitude of the illusion could in theory be measured through comparison of a close-up shot of the moon with a photograph containing both sun and moon, with the camera directed in a specified direction between them (although no equations are given). However, as they point out, in practice it is not feasible since even a wide-angle lens cannot capture both sun and moon in a photo with azimuth differences for which the illusion can be most clearly observed (between 90◦ and 180◦). Berry[1] proposed using a star chart, which is a zenith-center stereoscopic projection of the celestial sphere onto a flat surface, to define the moon tilt illusion as the angle between the projected great circle and a straight moon-sun line drawn on the same chart “mimicking how we might see the sky when lying on our back looking up”. Clearly, there exists a lack of consensus in the literature about the explanation of the moon tilt illusion and disagreement about the best way to describe it.
~
Astronomers rely upon the celestial sphere model for maps of the sky because locations of stars and constellations depend only on their right ascension and declination. For the topocentric model used for the sun and the moon, location is specified by azimuth and altitude. All objects in the sky are assumed to be located at the same distance from the observer, as if pasted upon the surface of an imaginery sphere surrounding the observer. Astronomers, for whom the celestial sphere model is a basic tool for mapping the stars, are not surprised by the apparently curved path of light from the sun to the moon because they know that straight lines in 3-D object space are transformed to great-circle arcs on the imaginary celestial sphere. ”
We are told that straight lines become curved when looking into the sky because of the "celestial sphere" which exists above our heads.
3D Model Example
A demonstration against this concept may be found in any 3D modeling program. Create a long straight line and place the camera at various positions and distances from it. At what point does the straight line become curved? The answer we have found is: At no point. A straight line in the distance will always be straight.
Alternatively, if the line were a green cone pointing at a yellow ball, the green cone would always point at the yellow ball.
In the above we took a picture of a 3D scene in various positions. With various positions and greater and greater distances from the scene, the cone will always point at the ball. One must wonder, why does the arrow always point at the ball? The assertion that arrows would not point at the things they are pointing at also implies that if you took a picture of any line in 3D space, that it would appear curved on the picture.
On this topic we receive arguments such as "What you are failing to consider is that the night sky is not a euclidean space; it's a curved surface." But just what is being described? In RET the space above and around it is not a "curved surface". It's not a surface at all. What reason is there to think that we would see it as a surface around us where straight lines become curves? This can only be seen as wild imagination from a desperate position.
Hence, the concept of a celestial sphere is seen to be a contrived concept bearing no relation to the 3D space which the Sun-Earth-Moon systems of astronomy are said to exist in. As there is no sphere around the Earth in RET upon which straight lines may become curved, it is again found that a geometric explanation for the Moon Tilt Illusion is unavailable. Astronomers disagree among themselves on the cause, with some speculating on a planetarium-like celestial sphere which does not exist in the physical Sun-Earth-Moon system.
Celestial Sphere Project
Our experts on astronomy provide us with a panoramic Moon Tilt Illusion scene with a Moon tilted upwards away from the Sun on the right hand side of the image cut into a "Celestial Sphere" to give us a better idea on "how things work in 3D space." Straight lines become curved on the Celestial Sphere.
Unfortunately, this example comes with a fictitious premise. The sky is not a sphere which the Sun, Moon, and lines of light rays rest against to cause artificial curvature. Straight lines will be straight in space above us, not 'curved on a celestial sphere'.
If the Sun and Moon can be connected in such a manner, it merely provides a small clue for the underlying mechanism, and does not imply that there is a "celestial sphere" above the Earth where "straight lines become curved". Such a mechanism is entirely unexplained and nonphysical in the Round Earth Theory.
Curving Lines on Celestial Sphere
The claim that lines curve on the Celestial Sphere above us is to claim that if we shine a laser into space that we will see it wrap around the dome and hit the opposite horizon.
If Dexter fires his laser beam into the sky and into space, will we see it 'wrap around' on the Celestial Sphere and hit the opposite horizon?
We are obliged to answer in the negative. The laser beam will not wrap around to the opposite horizon. We again see that the mechanism of a 'Celestial Sphere' is nonphysical and unexplained.
At amazingsky.com we find the following (Archive):
Caption: "The MSM’s bright laser pointer is useful for aiming the tracker at the North Celestial Pole, located about a degree away from Polaris in the direction of Alkaid, the end star in the Handle of the Big Dipper or Plough."
If the laser could continue forever into the distance, would it curve around on the Celestial Sphere and hit the horizon?
Predictive Equation
In The Moon Tilt Illusion (Archive) Professor Myers provides equations which can be used to predict the Moon's tilt in the Moon Tilt Illusion. Some have attempted to reference these equations as a piece of evidence that the Moon Tilt can be explained under the Round Earth Theory. Assessing the scheme of the model used, however, shows that it is not a Round Earth model.
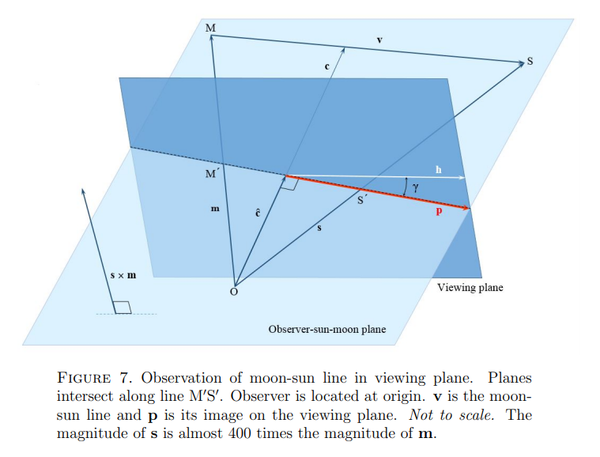
Viewing Plane
In Professor Myers' model the distant Moon and Sun are projected onto a "viewing plane" near the observer. Figure 7 on p.8 shows a diagram of this model:
In the above caption it is stated of the Moon and Sun that the "image is on the viewing plane". Is there a viewing plane above our heads in RET where bodies are projected upon? As we are not taught that there is a "viewing plane" close above our heads where the celestial bodies are projected, we must question the premise of the calculations.
Why is a "viewing plane" necessary? We see that the model is unrelated to the systems which are said to be in place.
Celestial Sphere
Previously, we had read that Professor Myers told us about the curving of light on the celestial sphere as cause of the Moon Tilt Illusion. He states:
- “ Astronomers, for whom the celestial sphere model is a basic tool for mapping the stars, are not surprised by the apparently curved path of light from the sun to the moon because they know that straight lines in 3-D object space are transformed to great-circle arcs on the imaginary celestial sphere. [2] ”
- “ The scientific explanation is based on the projection of a straight line onto the surface of a sphere [3] ”
- “ The moon tilt illusion is not described in astronomy textbooks because astronomers know that straight lines in object space become great circles on the celestial sphere. [4] ”
At the bottom of p.2 of his paper The Moon Tilt Illusion (Archive) Professor Myers explains that the celestial sphere is used as an axiom in the equations for the predictive portion:
“ Our aim is to derive an equation for the magnitude of the moon tilt illusion that is straightforward to apply to all configurations of sun and moon in the sky. The viewer’s expectation for the direction of incoming light is modeled using vector geometry, which is appropriate for treating 3-D straight lines such as the sun-moon light ray. Analyzing an illusion may seem trivial but the explanation of the moon tilt illusion requires knowledge of the perspective projection basis of human vision, vector algebra, and geometrical concepts such as orthographic projections, the celestial sphere, and geodesics. ”
Once we consider all of the above, including geometrical concepts such as the celestial sphere, upon which the celestial bodies are assumed to be resting on at different angles and where straight lines become curved, we can explain the Moon Tilt Illusion.
Distance to Sun and Moon Not Used
On p.9 we see statements that the distances to the Sun and Moon are not used and are avoided.
“ The value of the angle α is the same for the vectors m, s and z or their corresponding unit vectors, which are used in Eq. (11) to avoid having to know the actual distances of the moon and the sun from the observer. The moon and sun unit vectors... ”
Doing the Math
At the 42 minute mark of a video titled Moon Tilt Illusion (Doing the Math), which looks at the math in the Myers paper, the narrator explains that the distance from the earth to the sun does not matter, and that in this model the illuminated portion of the Moon will point in the same direction regardless of the distance of the Sun to the Earth. The illuminated portion of the Moon will always point in the same direction, whether the Sun is 0 or 100,000,000 units of measurement away from the observer.
A Simple Challenge
To those who do think that this model does represent a Round Earth model; a simple exercise is to go through the document and point out the page or section where the distance from the Earth to the Sun or the Earth to the Moon is expressed in the equations. We have found that the distances do not appear anywhere in the equations.
However, there is an angle and perspective difference between moving bodies which are close by and moving bodies which are millions of miles away. A Round Earth model should have Round Earth properties. Since the above predictive model does not use the Round Earth distances, and instead appeals to 'viewing planes', 'celestial spheres', and undefined distances, it cannot be a Round Earth model. The required geometry could be seen to act more as evidence against than for.
Conclusion
The Flat Earth Theory provides a geometric explanation for the Moon Tilt Illusion and the dome-like movement and orientation of the celestial bodies in the sky. Its astronomical model directly predicts the tilting of the Moon's phase independent of the Sun's direction.
The Round Earth Theory, in contrast, has difficulty with providing a working explanation for the Moon Tilt Illusion. Straight lines in normal space should cause the illuminated portion of the Moon to point at the Sun. The explanations for this appeal to questionable perspective explanations, visual field distortion, and lines which curve on a "celestial sphere". A perspective explanation has difficulty explaining seeing the Sun and Moon misaligned when viewed simultaneously, visual field distortion is not able to be replicated with objects other than the Moon, whereas a celestial sphere explanation is entirely immaterial and without a mechanism. In complete contradiction to popular dogma, it is the Round Earth Theory which has geometric difficulties, lacking explanatory power for common observations.
Celestial Sphere
Beyond the orientation of the Moon's illuminated area, this effect also applies to other celestial phenomena. The tails of comets, meteors, Aurora borialis, Milky Way, and path of the Moon and Sun in the sky are all affected and curved upon the Celestial Sphere. See: Celestial Sphere
Topics
Sunrise and Sunset - Sunrise and Sunset Main Page
- Electromagnetic Acceleration - EA Main Page
- Lunar Eclipse due to Electromagnetic Acceleration - The Lunar Eclipse occurs when the Moon moves beyond the Sun's light
- Celestial Sphere - The tails of comets, Aurora Borealis, Milky Way, and the path of the Moon and Sun are warped on a 'Celestial Sphere'
- Moon Tilt Illusion - Illuminated portion of the Moon does not point in the expected direction
- Moon Tilt Illusion Supplement - Discussion on the 'String Experiment' and 'Ball Experiment'
- High Altitude Horizon Dip - Horizon dip at high altitudes may suggest a bending of light