Equivalence Principle
The Equivalence Principle is a fundamental principle of physics which states that gravity operates as if the observer was in an upwardly accelerating frame of reference. Despite that it takes more force to move a more massive object through space (Newton's Second Law), when in free-fall bodies of different masses 'fall' at the same rate without exhibition of different inertial resistances, just as if the bodies were inert and the Earth were accelerating upwards into them. The Equivalence Principle is also used to explain why observers in free-fall feel weightless, rather than feeling their own weight pulling them down (ie. while in a Zero G plane). Experiments with light and atomic clocks at various scales have further confirmed the nature of the Equivalence Principle[1].
“ There is no experiment observers can perform to distinguish whether an acceleration arises because of a gravitational force or because their reference frame is accelerating. ”
—Douglas C. Giancoli, Physics for Scientists and Engineers with Modern Physics, p. 155.
Description
“ Whilst preparing a review article on his new special theory of relativity, [Einstein] became convinced that the key to the extension of the principle of relativity to accelerated motion lay in the remarkable and unexplained empirical coincidence of the equality of inertial and gravitational masses. To interpret and exploit this coincidence, he introduced a new and powerful physical principle, soon to be called the ‘principle of equivalence,’ upon which his search for a general theory of relativity would be based. ”
—John Norton, What was Einstein's Principle of Equivalence? (Archive)
“ Einstein himself thought the equivalence principle deeply mysterious. ‘Mass,’ he wrote, ‘is defined by the resistance that a body opposes to its acceleration (inert mass). It is also measured by the weight of the body (heavy mass). That these two radically different definitions lead to the same value for the mass of a body is, in itself, an astonishing fact.’ Francis Everitt of Stanford put it more forcibly. ‘In truth, the equivalence principle is the weirdest apparent fact in all of physics,’ he said. ‘Have you noticed that when a physicist calls something a principle, he means something he believes with total conviction but doesn’t in the slightest degree
understand.’ ”
—Nigel Calde, Magic Universe - A Grand Tour of Modern Science, 2005
“ This equivalence of the gravitational and inertial masses (which allows us to refer simply to 'the mass'), is a truly remarkable coincidence in the Newtonian theory. In this theory there is no a-priori reason why the quantity that determines the magnitude of the gravitational force on the particle should equal the quantity that determines the particle's 'resistance' to an applied force in general. ”
—General Relativity: An Introduction for Physicists
Thought Experiments Behind Einstein's Theory
A Space.com article Relativity: The Thought Experiments Behind Einstein's Theory (Archive) by astrophysicist Paul Sutter (bio) explains that under a plain interpretation of how Newtonian Gravity pulls on objects, a body with twice the mass of another should fall faster. Newtonian Gravity requires a separation of inertial and gravitational mass and their equivalence for bodies to fall equally. It is suggested that this is an ad-hoc mechanism to explain physical phenomena.
“ Einstein's first insight into the nature of gravity was to put a new twist on an old idea. In Isaac Newton's original mathematical description of gravity ("OG"?), there's an odd coincidence when it comes to the concept of "mass." In one famous equation, F = ma, mass is your inertia — how much oomph it takes to shove you along. In Newton's other equation on gravity, mass is more like gravitational charge — the level of attraction you might feel toward the Earth, for example.
Objects with twice the mass feel twice the attraction toward the Earth, and should therefore fall twice as quickly. But years back, Galileo Galilei had conclusively shown that they don't: Neglecting air resistance, all objects fall at the same rate regardless of their mass.
Thus for Newton's theory to work, inertial mass had to be the same as gravitational mass, but only by sheer coincidence: there was no reason for this equality to hold. For an object with twice the mass, the Earth may pull on it twice as strongly, but this is perfectly canceled out by the fact that it's now twice as hard to get the object moving. Inertial and gravitational masses move in perfect lockstep.
This odd correspondence had long been a puzzle in gravitational circles, but in 1907, Einstein took it one step further. The physicist imagined what would happen if you were to fall from a great height. Again neglecting air resistance, your inertial and gravitational masses would cancel, making you feel perfectly weightless, as if there were no gravity at all. But zero-gravity environments are precisely the playground of Special Relativity, the theory he had cooked up just a couple years prior that wove our conceptions of space and time into the unified fabric of spacetime.
To Einstein, this was a major clue. Lurking in the shadows of gravity was his precious special relativity and the essential concept of space-time, and what made that realization possible was the elevation of the equivalence between inertial and gravitational masses into a fundamental principle, rather than the awkward afterthought it had been. ”
4th Cosmology School at Cracow, Poland
See this slide from the Introduction to Cosmology by the 4th Cosmology School at Cracow, Poland (Archive):
Coincidence in General Relativity
The Equivalence Principle is also said by some to be a coincidence in General Relativity. See the following quotes.
Ryan Martin
On p.112 of Introductory Physics: Building Models to Describe Our World (Archive) by astrophysicist Ryan Martin (bio), Et al., it says:
“ As you recall, the weight of an object is given by the mass of the object multiplied by the strength of the gravitational field, g. There is no reason that the mass that is used to calculate weight, Fg = mg, has to be the same quantity as the mass that is used to calculate inertia F = ma. Thus, people will sometimes make the distinction between “gravitational mass” (the mass that you use to calculate weight and the force of gravity) and “inertial mass” as described above. Very precise experiments have been carried out to determine if the gravitational and inertial masses are equal. So far, experiments have been unable to detect any difference between the two quantities. As we will see, both Newton’s Universal Theory of Gravity and Einstein Theory of General Relativity assume that the two are indeed equal. In fact, it is a key requirement for Einstein’s Theory that the two be equal (the assumption that they are equal is called the “Equivalence Principle”). You should however keep in mind that there is no physical reason that the two are the same, and that as far as we know, it is a coincidence! ”
American Institute of Aeronautics and Astronautics
Another quote from a publication of the AIAA on p.99:
“ Newton proposed two formulas: the law of motion, F = ma, and the law of gravitation, F = GMm/r2. The mass, m, has two distinct meanings in the two formulas, one as the receptacle of inertia, the other as the source and receptacle of gravitation; yet somehow the two are identical. Stated another way, if mi and mg are respectively inertial and gravitational mass, then for any two bodies A and B, regardless of what substance they are, the quantity
- η = 2 [mi/mg)A - (mi/mgB]/[mi/mg)A + (mi/mg)B] (5)
appears to be identically zero. It was just this identity that Einstein denominated a principle (weak equivalence) and extended (strong equivalence) to all the laws of physics in accelerated frames, whether the acceleration is inertial or gravitational in origin. Strong equivalence is the basis on which it becomes possible in general relativity to represent gravitation by a curvature of spacetime. Contrary to what is sometimes thought, however, general relativity does not explain equivalence. The principle is an assumption that, once made, allows the effects of gravity to be represented thus. The phenomenon remains a mystery and still needs testing. ”
Anatoly Alekseyevich Logunov
Theoretical Physicist Anatoly Alekseyevich Logunov (bio) remarks:
https://pdfroom.com/books/the-theory-of-gravity/X623zYb6g4Z
“ GRT does not comply with the equivalence principle, does not explain the equality of the inert and active gravitational masses, and gives no unique prediction for gravitational effects. It does not contain the usual conservation laws of energy–momentum and of angular momentum of matter. ”
GRT = General Relativity Theory, as defined earlier in the paper:
“ Therein, also, critical comments are presented concerning general relativity theory (GRT), which still remain in force. ”
Classroom Aid - Equivalence Principle
The following video briefly describes the Equivalence Principle (Runtime: 5m):
Examples
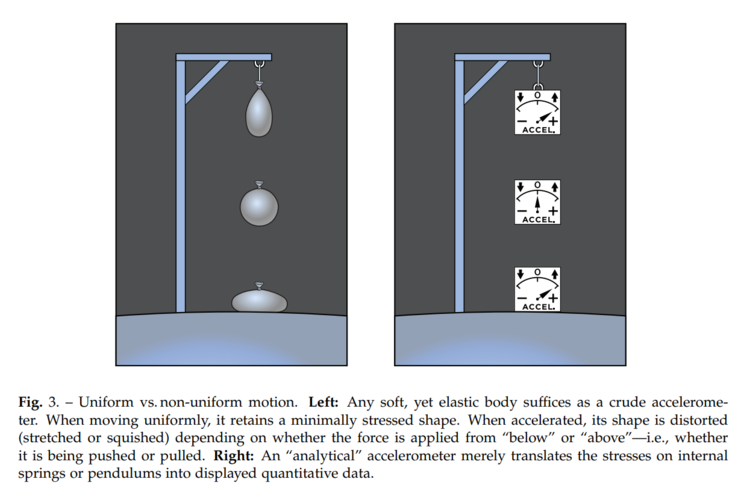
Water Balloon and Accelerometer
The effect of the surface's upwards acceleration can be seen in a hanging and falling water balloon (left) and a mechanical accelerometer (right).
http://gravityprobe.org/GravityProbe%20Links/Galileo-Undone-Mar-10-2020.pdf (Archive)
Monkey and the Hunter
https://web2.ph.utexas.edu/~gleeson/RelativityNotesChapter8.pdf (Archive)
8.3.1 The Monkey and the Hunter
“ There is a very popular demonstration that is performed in most high school and college introductory physics classes. There is a gun of some type that launches a projectile and a target object, usually a toy monkey, that can fall some distance. The gun and the monkey are rigged so that at the instant the gun fires the monkey is released to start to fall. ”
Figure 8.3: Monkey and the Hunter A popular lecture demonstration is to fire a projectile at a hanging toy monkey. The monkey is released at the instant that the gun is fired.
“ The class is usually asked where does the hunter aim. Since the monkey is falling, there is an argument that the hunter should aim below the initial position of the monkey to compensate for the finite time of flight of the projectile. On the other hand, the projectile has an arced trajectory and thus the aim should be above the current position. The correct answer is that the hunter should aim at the present position of the monkey. This is because once the gun is fired both the projectile and monkey are falling with an acceleration of g. In the frame accelerating down at a rate g, the effects of gravity are cancelled and thus neither the monkey nor the projectile have accelerated motion. In that frame, the projectile travels in a straight line and the monkey never moves. Note that if the aim is correct, no matter how small the projectile muzzle velocity, it will ultimately hit the monkey. This is an interesting pre-relativity example of the equivalence principle. ”
Science at the Amusement Park
https://web.archive.org/web/20200704180931/http://physics.gu.se/LISEBERG/callab.html
Carousel with Swings
“ A good starting point is the carousel with swings shown in Fig. 1. As the carousel rotates, the swings hang out from the vertical line, thereby enabling the chains to provide the force giving the required centripetal acceleration, while still counteracting the force of gravity. Take a moment consider which swings will hang out the most: the empty ones or the ones loaded with a child or with an heavy adult! In this situation students often pick the most heavily-loaded swings. They watch in amazement as the carousel starts - all swings (at the same radius) hang at the same angle, independent of load. ”
“ This is an eye-catching example of the equivalence principle: The angle is determined by the ratio between the centripetal force and the weight. Since the intertial mass (entering the centripetal force) and the gravitational mass (entering the weight, mg), are equal, the angle is independent of the mass. ”
Roland Eötvös
In Equivalence of Gravitational and Inertial Mass (Archive) by Benjamin Crowell, Ph.D. (bio), we read about Roland Eötvös' investigation into the Equivalence Principle:
“ We find experimentally that both gravitational and inertial mass are conserved to a high degree of precision for a great number of processes, including chemical reactions, melting, boiling, soaking up water with a sponge, and rotting of meat and vegetables. Now it's logically possible that both gravitational and inertial mass are conserved, but that there is no particular relationship between them, in which case we would say that they are separately conserved. On the other hand, the two conservation laws may be redundant, like having one law against murder and another law against killing people! ”
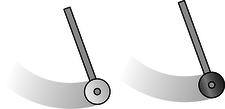
Figure a: The two pendulum bobs are constructed with equal gravitational masses. If their inertial masses are also equal, then each pendulum should take exactly the same amount of time per swing.
“ Here's an experiment that gets at the issue: stand up now and drop a coin and one of your shoes side by side. I used a 400-gram shoe and a 2-gram penny, and they hit the floor at the same time as far as I could tell by eye. This is an interesting result, but a physicist and an ordinary person will find it interesting for different reasons.
The layperson is surprised, since it would seem logical that heaver objects would always fall faster than light ones. However, it's fairly easy to prove that if air friction is negligible, any two objects made of the same substance must have identical motion when they fall. For instance, a 2-kg copper mass must exhibit the same falling motion as a 1-kg copper mass, because nothing would be changed by physically joining together two 1-kg copper masses to make a single 2-kg copper mass. Suppose, for example, that they are joined with a dab of glue; the glue isn't under any strain, because the two masses are doing the same thing side by side. Since the glue isn't really doing anything, it makes no difference whether the masses fall separately or side by side.2 ”
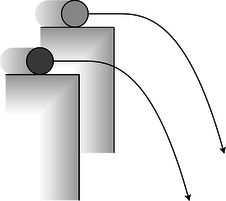
Figure b: If the cylinders have slightly unequal ratios of inertial to gravitational mass, their trajectories will be a little different.
“ What a physicist finds remarkable about the shoe-and-penny experiment is that it came out the way it did even though the shoe and the penny are made of different substances. There is absolutely no theoretical reason why this should be true. We could say that it happens because the greater gravitational mass of the shoe is exactly counteracted by its greater inertial mass, which makes it harder for gravity to get it moving, but that just leaves us wondering why inertial mass and gravitational mass are always in proportion to each other. It's possible that they are only approximately equivalent. Most of the mass of ordinary matter comes from neutrons and protons, and we could imagine, for instance, that neutrons and protons do not have exactly the same ratio of gravitational to inertial mass. This would show up as a different ratio of gravitational to inertial mass for substances containing different proportions of neutrons and protons.
Galileo did the first numerical experiments on this issue in the seventeenth century by rolling balls down inclined planes, although he didn't think about his results in these terms. A fairly easy way to improve on Galileo's accuracy is to use pendulums with bobs made of different materials. Suppose, for example, that we construct an aluminum bob and a brass bob, and use a double-pan balance to verify to good precision that their gravitational masses are equal. If we then measure the time required for each pendulum to perform a hundred cycles, we can check whether the results are the same. If their inertial masses are unequal, then the one with a smaller inertial mass will go through each cycle faster, since gravity has an easier time accelerating and decelerating it. With this type of experiment, one can easily verify that gravitational and inertial mass are proportional to each other to an accuracy of 10−3 or 10−4.
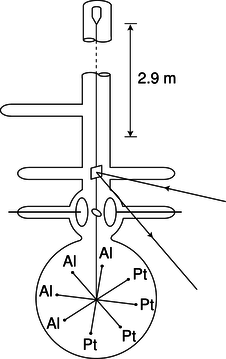
In 1889, the Hungarian physicist Roland Eötvös used a slightly different approach to verify the equivalence of gravitational and inertial mass for various substances to an accuracy of about 10−8 , and the best such experiment, figure d, improved on even this phenomenal accuracy, bringing it to the 10−12 level.3 In all the experiments described so far, the two objects move along similar trajectories: straight lines in the penny-and-shoe and inclined plane experiments, and circular arcs in the pendulum version. The Eötvös-style experiment looks for differences in the objects' trajectories. The concept can be understood by imagining the following simplified version. Suppose, as in figure b, we roll a brass cylinder off of a tabletop and measure where it hits the floor, and then do the same with an aluminum cylinder, making sure that both of them go over the edge with precisely the same velocity. An object with zero gravitational mass would fly off straight and hit the wall, while an object with zero inertial mass would make a sudden 90-degree turn and drop straight to the floor. If the aluminum and brass cylinders have ordinary, but slightly unequal, ratios of gravitational to inertial mass, then they will follow trajectories that are just slightly different. In other words, if inertial and gravitational mass are not exactly proportional to each other for all substances, then objects made of different substances will have different trajectories in the presence of gravity. ”
Figure c: A simplified drawing of an Eötvös-style experiment. If the two masses, made out of two different substances, have slightly different ratios of inertial to gravitational mass, then the apparatus will twist slightly as the earth spins.
“ A simplified drawing of a practical, high-precision experiment is shown in figure c. Two objects made of different substances are balanced on the ends of a bar, which is suspended at the center from a thin fiber. The whole apparatus moves through space on a complicated, looping trajectory arising from the rotation of the earth superimposed on the earth's orbital motion around the sun. Both the earth's gravity and the sun's gravity act on the two objects. If their inertial masses are not exactly in proportion to their gravitational masses, then they will follow slightly different trajectories through space, which will result in a very slight twisting of the fiber between the daytime, when the sun's gravity is pulling upward, and the night, when the sun's gravity is downward. Figure d shows a more realistic picture of the apparatus. ”
Figure d: A more realistic drawing of Braginskii and Panov's experiment. The whole thing was encased in a tall vacuum tube, which was placed in a sealed basement whose temperature was controlled to within 0.02°C. The total mass of the platinum and aluminum test masses, plus the tungsten wire and the balance arms, was only 4.4 g. To detect tiny motions, a laser beam was bounced off of a mirror attached to the wire. There was so little friction that the balance would have taken on the order of several years to calm down completely after being put in place; to stop these vibrations, static electrical forces were applied through the two circular plates to provide very gentle twists on the ellipsoidal mass between them.
General Relativity and Accelerating Upwards
The Equivalence Principle is a fundamental tenet of General Relativity, which describes that the surface of the Earth is accelerating upwards through curved space-time to cause the Equivalence Principle effects as experienced on Earth. The following citations describe why space was decided to be curved in the Round Earth Theory.
Gravity: A Very Short Introduction
From Gravity: A Very Short Introduction (Archive) by Cosmologist Timothy Clifton (bio), we read:
“ Consider a skydiver jumping out of an airplane. The skydiver falls freely, up to the effects of air resistance. According to Einstein, the skydiver's path is the straightest line possible through the curved space-time around the Earth. From the skydiver's perspective this seems quite natural. Except for the air rushing past her, the skydiver feels no perturbing forces at all. In fact, if it weren't for the air resistance, she would experience weightlessness in the same way that an astronaut does in orbit. The only reason we think the skydiver is accelerating is because we are used to using the surface of the Earth as our frame of reference. If we free ourselves from this convention, then we have no reason to think the skydiver is accelerating at all.
Now consider yourself on the ground, looking up at the falling daredevil. Normally, your intuitive description of your own motion would be that you are stationary. But again this is only because of our slavish regard to the Earth as the arbiter of what is at rest and what is moving. Free yourself from this prison, and you realize that you are, in fact, accelerating. You feel a force on the soles of your feet that pushes you upwards, in the same way that you would if you were in a lift that accelerated upwards very quickly. In Einstein's picture there is no difference between your experience sanding on Earth and your experience in the lift. In both situations you are accelerating upwards. In the latter situation it is the lift that is responsible for your acceleration. In the former, it is the fact that the Earth is solid that pushes you upwards through space-time, knocking you off your free-fall trajectory. That the surface of the Earth can accelerate upwards at every point on its surface, and remain as a solid object, is because it exists in a curved space-time and not in a flat space.
With this change in perspective the true nature of gravity becomes apparent. The free falling skydiver is brought to Earth because the space-time through which she falls is curved. It is not an external force that tugs her downwards, but her own natural motion through a curved space. On the other hand, as a person standing on the ground, the pressure you feel on the soles of your feet is due to the rigidity of the Earth pushing you upwards. Again, there is no external force pulling you to Earth. It is only the electrostatic forces in the rocks below your feet that keep the ground rigid, and that prevents you from taking what would be your natural motion (which would also be free fall).
So, if we free ourselves from defining our motion with respect to the surface of the Earth we realize that the skydiver is not accelerating, while the person who stands on the surface of the Earth is accelerating. Just the opposite of what we usually think. Going back to Galileo's experiment on the leaning tower of Pisa, we can now see why he observed all of his cannonballs to fall at the same rate. It wasn't really the cannonballs that were accelerating away from Galileo at all, it was Galileo that was accelerating away from the cannonballs! ”
Why Is Spacetime Curved?
In a section titled Why Is Spacetime Curved? of the book Time Travel in Einstein’s Universe by John Richard Gott III (bio), professor of astrophysical sciences at Princeton University, we read:
“ A famous (perhaps apocryphal) story about Einstein describes one occasion when he fell into conversation with a man at the Institute for Advanced Study at Princeton. During their chat, the man suddenly pulled a little book from his coat pocket and jotted something down. Einstein asked, “What is that?" “Oh,” the man answered, “it's a notebook I keep, so that any time I have a good idea I can write it down before I forget it.” “I never needed one of those," Einstein replied. “I only had three good ideas.”
One of them occurred to him in 1907—what he would later call the “happiest” idea of his life. Einstein noted that an observer on Earth and an observer on an accelerating spaceship in interstellar space would have the same sensations. Follow this chain of thought to see why. Galileo had shown that an observer dropping two balls of different mass on Earth sees them hit the floor at the same time. If an observer in an accelerating rocket in interstellar space performed the same experiment, dropping two balls of different mass, they would float motionless in space—but, since the rocket was firing, the floor of the spaceship would simply come up and hit both of them at once. Both observers thus should see the same thing. In one case, it is the result of gravity; in the other case, it is caused by an accelerating floor with no gravity involved. But then Einstein proposed something very bold—if the two situations looked the same, they must be the same. Gravity was nothing more than an accelerated frame-of-reference. Likewise, Einstein noted that if you get in an elevator on Earth and cut the cable, you and everything in the elevator will fall toward Earth at the same rate. (Galileo again—objects of different mass all fall at the same rate.) So, how do things look to you in the falling elevator? Any object you drop will float weightless in the elevator—because you, the object, and the elevator are all falling at the same rate together. This is exactly what you would see if you were in a spaceship floating in interstellar space. All the objects in the spaceship, including you, would be weightless. If you want to experience weightlessness just like an astronaut, all you have to do is get in an elevator and cut the cable. (This works, of course, only until the elevator hits bottom.)
Einstein's assertion that gravity and acceleration are, the same—which he called the equivalence principle—was influenced, no doubt, by his previous success in equating the situation of a stationary magnet and a moving charge with that of a stationary charge and a moving magnet. But if gravity and accelerated motion were the same, then gravity was nothing but accelerated motion. Earth's surface was simply accelerating upward. This explained why a heavy ball and a light ball, when dropped, hit the floor at the same time. When the balls are released, they just float there—weightless. The floor (Earth) simply comes up and hits them. What a remarkably fresh way of looking at things!
Still one must ask how Earth’s surface could be accelerating upward (away from Earth's center) if Earth itself is not getting bigger and bigger with time like a balloon. The only way the assertion could make sense is by considering spacetime to be curved.
Einstein proposed that mass and energy cause spacetime to curve. It took him 8 years of hard work to derive the equations governing this. He had to learn the abstruse geometry of curved higher dimensional spaces. He had to learn about the Riemannian curvature tensor—a mathematical monster with 256 components telling how spacetime could be curved. This was very difficult mathematics, and Einstein ran upon many false leads. But he didn't give up because he had great faith in the idea. ”
Relativity Visualized
“ Einstein’s view of gravity is that things don’t fall; the floor comes up! ”
—Epstein, Lewis Carroll: Relativity Visualized. (Insight Press, San Francisco, 1988) pp. 65 ff.
Tony Goldsmith
Tony Goldsmith, author of a mass-media book Space-time for Absolute Beginners and his Absolute Beginner book series, explains the Equivalence Principle as follows (Archive):
“ When you are in a lift you may be accelerated. Where is this coming from? It is the lift pushing you up.
Einstein said that the Earth does the same as a lift (which has an acceleration of g). The Earth isn't in the way; it is doing the pushing. This is his Equivalence Principle. ”
Why Gravity is NOT a Force
A popular science video by Veritasium with over 10 million views, Why Gravity is NOT a Force, explains at the 9:57 mark how in General Relativity you accelerate upwards without changing your spatial coordinates with the General Relativity equation:
“ But if I'm accelerating up and so is everyone else around the world and presumably the whole surface of the Earth, then shouldn't the whole earth be expanding?
No. It is possible for you to be accelerating even though your spatial coordinates are not changing. I will show you one equation from General Relativity...
[equation]
...so in curved space-time you have to accelerate just to stand still. ”
Inner Life of Numbers
In a book on how math relates to the universe One to Nine: The Inner Life of Numbers by mathematician Andrew Hodges (bio), he describes that the earth's surface is accelerating upwards against your feet in the geometry of curved space-time (Archive):
“ Earth's mass curves the geometry of space-time in such a way that the Earth's surface is always accelerating upwards at 9.81 m/sec^2 and so presses on your feet. Weight doesn't exist, but the Earth's electromagnetic forces push harder on fat boys than on slim. This sounds crazy, but it is no crazier than the fact that if you steam straight ahead on a sphere you will end up back where you started. Such things are made possible by curvature. ”
Earth’s Surface Accelerates Up (and Out)
A physics student, Berry, came across this subject and made us a brief paper about what he learned in his upper level physics classes, showing the math on how in the globe model of gravity the surface of the earth is actually accelerating upwards (Archive).
“ This paper uses the Schwarzchild geometry utilized by the current globe Earth model to show that the surface of the Earth is accelerating upwards. ”
Experiments
A great many experiments have taken place in the effort to find violation of the Equivalence Principle. The following are of interest:
- Gravitational Time Dilation - Time dilates in accordance with the uniform prediction of the Equivalence Principal to various heights
- Time Dilation by Latitude - The Equivalence Principle is used to explain why time does not dilate at different latitudes due to the different latitudinal speeds of Earth
- Vertical Michelson-Morley Experiment - Light velocity changes when photons are directed upwards or downwards
- Pound-Rebka Experiment - The frequency of light red-shifts or blue-shifts when moving upwards or downwards in accordance with Doppler Shift
Variations in Gravity
It is often claimed that gravity varies by location on a larger scale. An assessment finds that the experiments either do not show variations, show unexpected results, or are contradicted by other experiments. See Variations in Gravity
See Also
Flat Earth Gravity Topics
- Universal Acceleration - The Universal Accelerator Main Page
- Equivalence Principle - Gravity behaves as if the Earth is accelerating upwards
- Evidence for Universal Acceleration - Experiments and background foundation showing that Earth is accelerating upwards
- Variations in Gravity - Various experiments have failed to find variations in gravity or violations of the Equivalence Principle
Round Earth Gravity Topics
- Weight Variation by Latitude - An uncontrolled weight change experiment which is not performed in a vaccum chamber
- Cavendish Experiment - An inconsistent short range attraction experiment
- Gravimetry - Gravimeters are described to be seismometers by mainstream sources
- Isostasy - The mass attraction of mountains and continents does not behave in accordance with 'gravity'