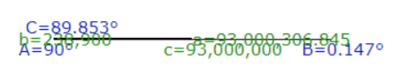Moon Tilt Illusion Supplement
The Moon Tilt Illusion Supplement page addresses some of the common counterarguments related to the Moon Tilt Illusion. Specifically, the String Experiment alleges that a string will demonstrate the direction of the Moon when held up against the Moon, the Ball Experiment alleges that a small ball held up against the Moon showing matching directions shows that a perspective illusion is occurring, and the Higher Sun Argument says that the Moon being illuminated from a higher position is caused by the Moon seeing the Sun at a higher position than the observer does.
String Experiment
As justification for the Moon Tilt Illusion we are told to take a piece of sting and to hold it across the ecliptic, the path which the Sun and Moon move across the sky, and observe that the direction of the Moon appears to connect to the Sun in the sky.
It has been argued that the string experiment shows that the bodies do actually point at each other. An illusion of some type is occurring and the string experiment "breaks the illusion," demonstrating that the illuminated portion of the Moon is actually pointing at the Sun. If it was not pointing at the Sun then it would not be possible to hold a straight piece of string along that path.
As a reply to this, consider the following scenario:
- You are laying down on the ground on your back, facing upwards, and at the edges of your vision see the top of a vertical pine tree on one side of your vision, and the top of a cabin on the other. You take out a string and connect them together across your vision. Have you proved that the tree is pointing at the cabin?
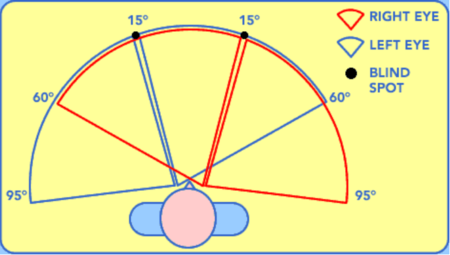
If you are laying down on the ground on your back and see the Moon pointing upwards on one side of your vision and see the Sun setting at the horizon on the other, a string connecting the two will no more prove that the Moon is pointing at the Sun than it would prove that a tree is pointing at a cabin. When you lay on your back you can see 190 degrees of space1,2. Just because an object at one side might be pointing "up" at another object at the other side, it doesn't mean that they are pointing at each other.
Footnotes
- 1 "our eyes sit in the front of our head, allowing us to see about 60 percent of world in front of us with both eyes, at the compromise that we can only see at maximum about 190 degrees around us (Block 1969; Wolfe 2006)" – Human Spatial Navigation, 2018, p.73
- 2 Explanatory image from https://www.vision-and-eye-health.com/visual-field.html (Archive) -
Fish Bowl Diagram
When wrapped around the observer, this panoramic view of the moon tilt illusion:
Turns into this, with an added airplane for reference:
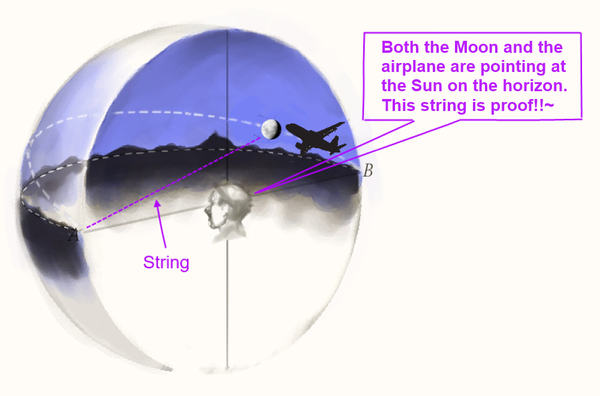
Art Credit: Todd Lockwood
In the above example both the Moon and airplane are on the ecliptic and on opposite sides of the Sun near point B. The Sun is on the horizon at point A. The Moon and airplane are not actually pointing at the Sun. The string merely connects them two dimensionally across a 'sphere of vision' exactly like the tree-cabin example.
If the airplane was actually pointing at the Sun in the above example, then when looking at the airplane face on, with the Sun on the horizon to your back, you should see the airplane pointed at you and tilted downwards towards the opposite horizon behind you. The same would also apply for the Moon. If the Moon were pointing at the Sun then when you face the Moon its illumined portion should point downwards at the Sun at the horizon behind you, just as an airplane would. Thus, we see that this assertion that the string experiment demonstrates that an illusion is occurring and that bodies are pointing at each other is erroneous.
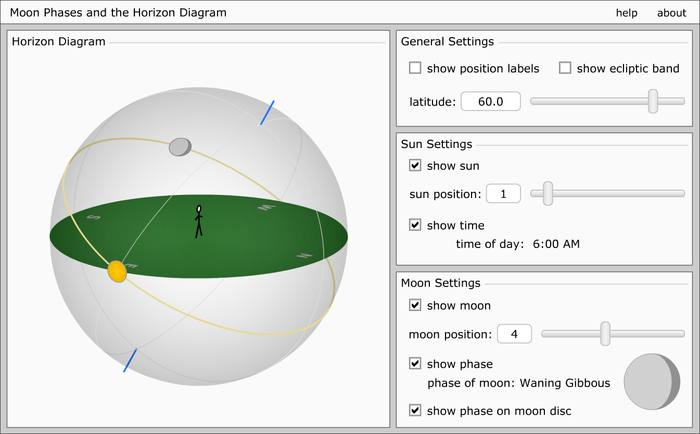
University of Nebraska Simulation
A fish-bowl type simulation of the Moon Tilt Illusion can also be seen in University of Nebraska-Lincoln's Moon Phases and the Horizon Diagram - "Provides a method of learning the correlation between the phase of the moon, the time of day, and the position of the moon in the sky." (.swf Archive Note: May need a swf player to play)
In this simulation the direction of the Moon follows the ecliptic as it progresses across the sky. Adjusting the sliders it is seen that when the Moon is rising its phase points upwards, at Midmoon the phase makes a right angle in the sky, and at setting the phase points downwards, along the yellow ecliptic.
In the above image, if the observer in the scene were to hold a water bottle at arm's length up against the Moon, aligning the direction with where the light appeared to be coming from, it would appear that the water bottle was pointing upwards into space away from the Sun. And per the 'string experiment', if the observer were to take a string and connect the Moon to the Sun across the yellow ecliptic, the Moon's phase would connect with the Sun.
String Experiment Not Reliable
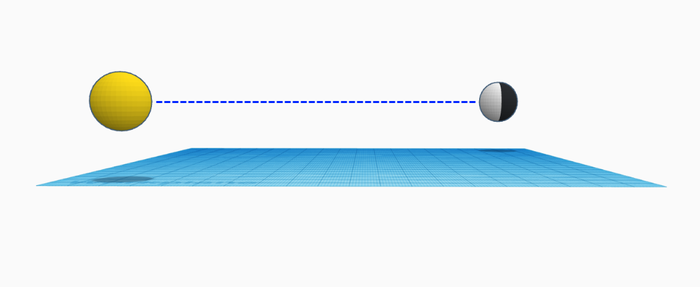
In the below scene we have a Moon misaligned from the Sun.
Changing the view to another position, we can connect a string between the two. Does this ability to connect a string prove that the Moon is pointing at the Sun?
We thus see that the string experiment is unable to distinguish whether a body is pointing at something else. It may provide a clue showing the adjacent nature of the phase with the ecliptic, but it does not show the absolute direction of bodies.
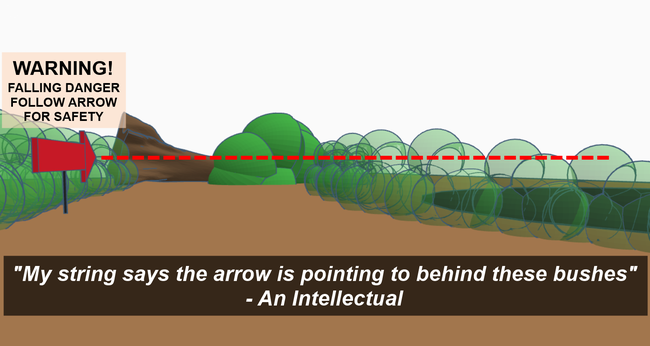
Arrow-Pit Example
Another example involves a warning arrow near a dangerous pit. The assertion that a string reveals that something is pointing at something else could lead to deadly results.
Elevated view:
First Person View:
Ball Experiment
Another justification of the Moon Tilt Illusion is the "ball experiment". A small ball is held up to the sky and the observer is able to position himself so that the phase and direction on the ball matches the Moon in the background. It is claimed that this shows that the illusion can be replicated.
Pencil Perspective Example
The effect which causes the phase of the ball to point upwards is a perspective effect. Positioning one's self beneath an object will cause the object to change orientation and point upwards.
By lowering your position beneath an object, it will point upward. This effect does not show that a tilted object is always being tilted upwards with the mechanism of perspective, however.
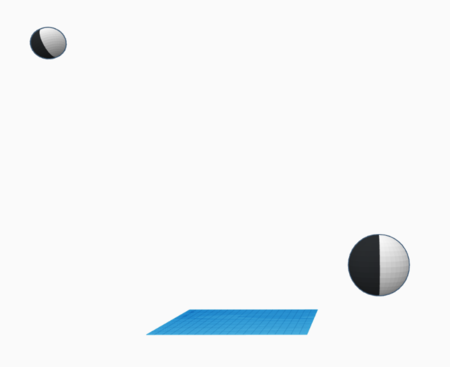
Misaligned Moons Example
It is also possible to cause a foreground object to tilt upwards to match an object that is physically tilted upwards in the background. In the below scene we have a foreground Moon physically misaligned with a Moon further in the background.
By repositioning the camera to a position beneath the foreground Moon we can get the foreground object to match the background object. Does this prove that the background object is tilted upwards to perspective?
A similar example with cones for reference may be seen here
California Bay Area Test
The following is an observation made from the California Bay Area which provides more scene references than the typical 'ball experiment' found on the internet.
https://forum.tfes.org/index.php?topic=17844.0
“ Bay Area California, Feb 21st, 2021, pictures taken around 5:27 PM PST with a Google Pixel 3 XL Phone.
- Image 1
- I placed the ball on a post along the side of a road. The sun was shining from a horizontal direction. The ball is half lit.
- Full Size: https://i.imgur.com/6AMa1fZ.jpg
- Image 2:
- Viewpoint from behind the ball, looking at Sun:
- Full Size: https://i.imgur.com/dahZJsy.jpg
- Image 3:
- From a position front of the ball, with our back to sun, we can see that the illuminated portion of the Moon pointing upwards in the background. See Full Size for detail.
- Full Size: https://i.imgur.com/yXGCLyR.jpg
- Image 4:
- Closeup of the Moon in the background, while zooming in the device created a digital leveling tool on the screen to help ensure the device was level. Compare the orientation to the Moon in the Full Size Image 3 above.
- Full Size: https://i.imgur.com/eSmtd9N.jpg
- Image 5:
- Next I moved my position to below the ball and the top of the post, to get the ball to point upwards via a close range perspective effect. I could have done a better job at getting the phase to match, by moving the camera around. But it was easy to move the camera downwards to get the illuminated portion to point upwards:
- Full Size: https://i.imgur.com/rSV2mAx.jpg
- Image 6:
- Finally, I turned the device and placed the ball across the screen from the sun on a wide frame. The illuminated portion pointed at the Sun.
- Full Size: https://i.imgur.com/BNazZl6.jpg
From the above images we can position the camera below the ball so that the illuminated portion of the ball points upwards in a manner similar to the Moon in the background. However, this does nothing to show that the Moon is actually tilted upwards with the same perspective effect. The perspective effect can tilt things upwards with careful manipulation of viewpoints, but in regards to its effect on the Moon, it is unable to explain why it is sometimes possible to view the Moon and Sun simultaneously while misaligned to each other.
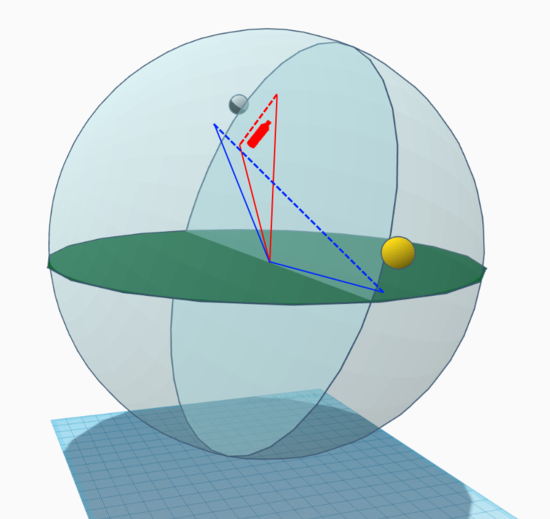
Scene Diagram
The following diagram resembles the above observation:
If we were to take a water bottle (red) and hold it out at arm's length to match the Moon's orientation and where the light is coming from, it would appear that both Moon and water bottle are pointing out into space and not at the Sun.
If we were to take a string (blue) and align it with the ecliptic, the path near where the Sun and Moon travel across the sky, the string might be able to hit the Sun, but this 'string experiment' is unable to distinguish whether the string is aligning with the body you are putting it against. The top of a tall vertical pine tree near the observer could also be made to "point" at the Sun by stretching a string across to it.
Spherical Directions
It is next argued that if we hold up and align the ball with the Moon in the sky that it will point in the same direction, and that this shows that the Moon must be tilting upwards to a perspective effect. Although it is questionable whether the phases always exactly match up (Compare the ball and Moon phases closely in the first ball experiment example), in regards to directions, it is seen that this perspective effect will also orient bodies in the same direction as the directions on the outside surface of a sphere.
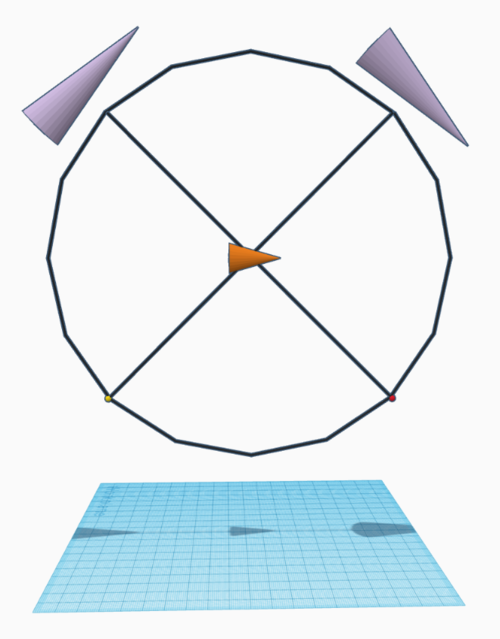
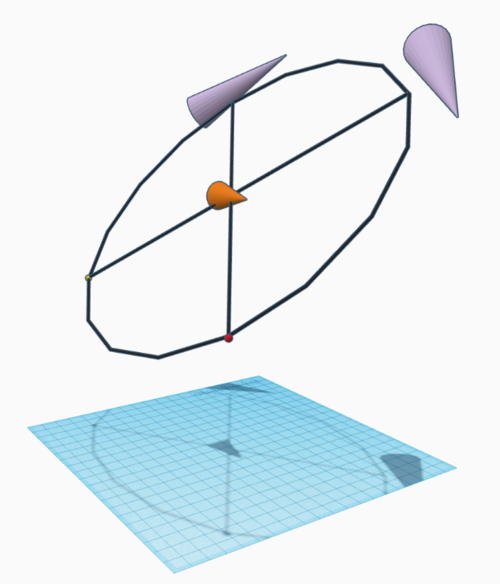
Below we have an orange cone which points horizontally and purple cones which follow the directions of the circle (representing part of a celestial sphere) around the orange cone, which are angled at +45 or -45 degrees in relation to the horizontal.
The following views are from the positions of the Red Pointer and Yellow Pointer:
Next we rotate the entire mechanism on its horizontal axis, 45 degrees to the right in relation to vertical:
From the views of the Red and Yellow Pointers we again see that the middle cone points in the same direction as the cones on the outside of the circle:
The changing angles of perspective of the orange cone matches the directions on the outside of a sphere when the bodies are aligned. This perspective experiment is unable to distinguish whether something is really tilting around you on a sphere or not.
Note: The orange cone illustrates where an object is pointing and how it changes direction to perspective. See this linked example which shows a half-colored sphere changing direction in tandem with a cone as the camera moves (Archive).
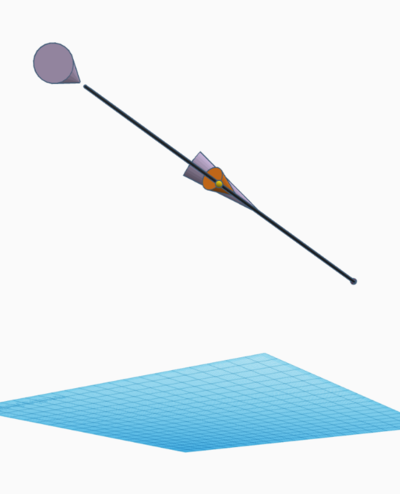
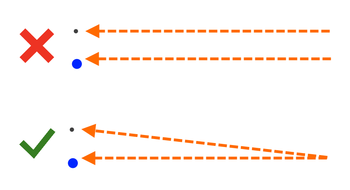
Phase Comparison
In the previous scene we saw purple and orange cones that point in the same general direction when aligned as seen by the observer, but the foreground and background objects were not in the same orientation. The observable directions they point towards is generally the same, but they are actually pointing in different directions. In the case with the Ball Experiment, the observable directions are the same, but the orientation of the Moon and the ball are different. This is evidence that the Moon is not undergoing the same perspective effect as the ball.
In the Ball Experiment the ball and Moon point in the same observable directions, but have different phases. From the orientation of the phases one can tell that the ball is pointing at a source lower than the Moon.
Since the Moon has a more crescent phase, it shows that the phase of the Moon is in a different orientation than the phase of test object.
If the ball and the Moon were undergoing the same perspective effect, and were pointing in the same direction, then the phase of the Moon should match the phase of the ball. If the ball were to recede and increase distance from the observer (and grow in size so that the observer could still see it), then the orientation of the phase should remain the same in its duration.
In the above we see that a receding half-illuminated ball should maintain its orientation. Since the orientation of the objects is not the same in the Ball Experiment, this is evidence that the orientation of the objects and light sources are not pointing in the same direction.
While true that the Sun's rays are not hitting both the observer and the Moon exactly horizontal at the displacement and distances involved, the RE Sun-Earth distance is of a significant size that Moon should only be pointing downwards at the Sun an extra small amount of about 0.147 degrees (see below Triangle Calculator section).
Higher Sun Argument
As response to the Moon Tilt Illusion it is sometimes argued that the illuminated portion of the Moon is misaligned to the Sun since Sun's light is parallel and hitting the Earth-Moon system as a whole from the side, and so the Moon will see a higher Sun than an observer on the Earth. The Sun will appear from a different position in space to the Moon, causing the Moon's illuminated area to point to a position above the Sun that we see from Earth.
In contrast to this argument, the angles are not perfectly parallel under the Round Earth system. When assessing the parallax displacement between an observer on Earth and an observer on the Moon the Sun will be in essentially the same point in space.
Angular Diameter Example
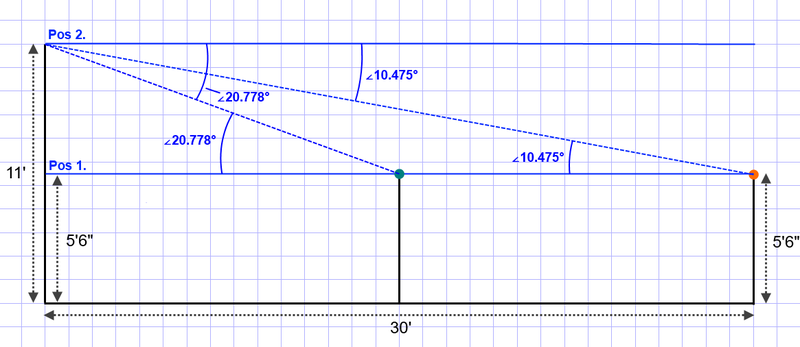
As an example, if your eye is at an altitude of 5 feet, 6 inches, and there is an object, say a Green Ball on a post 15 feet away from you at the same altitude, and an Orange Ball on a post 30 feet away from you, which are both also at altitudes of 5 feet, 6 inches, then the position of both the green and orange balls will be parallel on the horizontal. The path to those objects will be at your eye level.
Next, lets say that you step on a boulder that is 5 foot, 6 inches in height. The new altitude of your eye is 11 feet in height. We know that the green and orange balls are on posts which are 5 ft 6 in below that 11 foot elevation where it would need to be to be parallel to the eye.
In order to find the position of the green and orange balls in degrees below eye level, we can use an angular diameter calculator to calculate the missing space above the green and orange ball, to determine how far below eye level those balls will be to the observer.
For the Green Ball, 5.5 feet of vertical space at 15 feet produces an angular diameter of 20.778 degrees. For the Orange Ball, 5.5 feet of vertical space at 30 feet produces an angular diameter of 10.475 degrees.
Diagram
We see that as a body moves further from you, it gets closer to your eye level, and displaces fewer degrees in space.
Next adopt the above to the Earth and Moon in the RE system from the previous diagram with the overhead Moon misaligned with the sun setting into the horizon. In order to calculate the displacement of the Sun in the between observers on Earth and the Moon we may use the angular diameter calculator with the distances involved in miles.
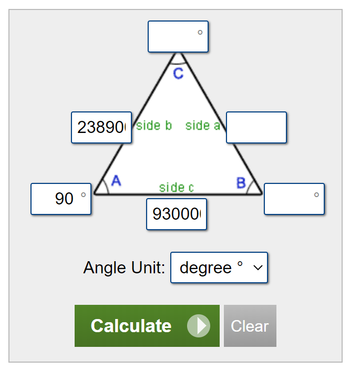
Input
g: 238900
r: 93000000
Output
a: 0.147 degrees
If the observer was able to move from the Earth to the Moon the Sun would be seen from essentially the same position in space. The diagram of the Sun appearing in two different places may be misleading, as it does not show the entire scene and the angles are not exactly parallel to the Sun.
Triangle Calculator
Next, we look at a triangle calculator, which will compute the missing values in a triangle:
We put in the distances in miles to the RE Moon at Side b, the distance to the RE Sun at Side c, and 90 degrees at the observer at Angle A. This produces the following:
We see a very thin Right Scalene Triangle diagram. We see that the angle displacement of the Sun at Angle B is 0.147 degrees, as previously seen in the angular diameter calculator. We also see that Moon at Angle C is pointing downwards at 89.853 degrees; not exactly parallel to the baseline.
The Sun is not actually shining on the Earth and Moon in a parallel manner, but at slightly different angles.
Triangle Diagram
Now, consider the above thin Right Scalene Triangle diagram which was generated by the Triangle Calculator:
If the object at Angle C Moon position was a Green Arrow pointing at the center of the Sun (Angle B), and if we could see both the Green Arrow and Sun at once in our field of vision, essentially the whole scene, like in the observation by astrophotographer Jerry Lodriguss [1], would the the Green Arrow point at the Sun?
This should be true regardless of the shape of the triangle, and demonstrates the expectation that the illuminated portion of the Moon should point at the Sun when viewed simultaneously. The Green Arrow should not point at a different spot in space.
Alignment with Sun Center
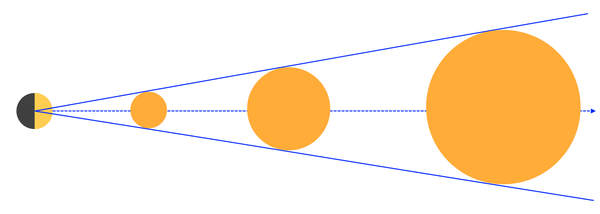
Finally, it is suggested that since the Sun is so large and the rays are essentially parallel to the relatively small Earth-Moon system at their distant location from the Sun, that the illuminated portion of the Moon is not necessarily pointing at the center of the Sun (restatement of premise).
Consider a situation where we have only have two bodies: The Moon and a Sun. The Sun starts as the size of the Moon and near to it. The illuminated portion of the Moon will point at the center of that Sun. If the Sun continuously recedes in distance away from the Moon and grows in size geometrically in a linear fashion, will the Moon ever not point at the center of the Sun?
Hence we see that, with only two bodies, the Moon will always point at the Sun's center, regardless of distance or size. There is no real reason for it to point anywhere else. From the position of the central hotspot upon the Moon's surface it will see the Sun directly 'overhead', and will be illuminated from directly 'overhead', regardless of how the Sun recedes or grows. The addition of an Earth somewhere around the Moon should not matter in regards to where the illuminated portion of the Moon points.
Back to: Moon Tilt Illusion - Higher Sun Argument
Topics
Sunrise and Sunset - Sunrise and Sunset Main Page
- Electromagnetic Acceleration - EA Main Page
- Lunar Eclipse due to Electromagnetic Acceleration - The Lunar Eclipse occurs when the Moon moves beyond the Sun's light
- Celestial Sphere - The tails of comets, Aurora Borealis, Milky Way, and the path of the Moon and Sun are warped on a 'Celestial Sphere'
- Moon Tilt Illusion - Illuminated portion of the Moon does not point in the expected direction
- Moon Tilt Illusion Supplement - Discussion on the 'String Experiment' and 'Ball Experiment'
- High Altitude Horizon Dip - Horizon dip at high altitudes may suggest a bending of light