Difference between revisions of "Celestial Sphere"
Tom Bishop (talk | contribs) |
Tom Bishop (talk | contribs) |
||
| Line 34: | Line 34: | ||
{{cite|Think of the sky as painted, or projected, onto the inside of a dome--like a planetarium dome.}} | {{cite|Think of the sky as painted, or projected, onto the inside of a dome--like a planetarium dome.}} | ||
| + | |||
| + | ==On the Evolution of the Heavenly Spheres== | ||
| + | |||
| + | A doctoral thesis explains that the the transformation of straight lines into curves on the celestial sphere has been known since antiquity. | ||
| + | |||
| + | '''On the Evolution of the Heavenly Spheres'''<br> | ||
| + | An Enactive Approach to Cosmography<br> | ||
| + | by David McConville | ||
| + | |||
| + | [https://pdfs.semanticscholar.org/ea59/3de5dae8f377560f84480618aff74889250d.pdf Full Text Link] ([https://web.archive.org/web/20191002204552/https://pdfs.semanticscholar.org/ea59/3de5dae8f377560f84480618aff74889250d.pdf Archive]) | ||
| + | |||
| + | p.40 | ||
| + | |||
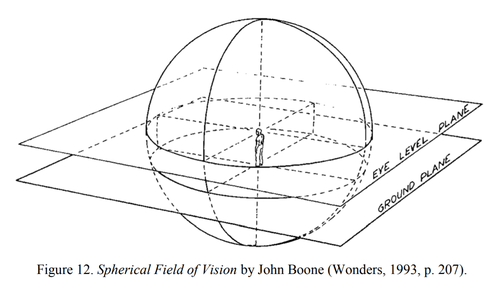
| + | [[File:Spherical Field of Vision.png|500px]] | ||
| + | |||
| + | {{cite|Though analysis of ‘one-point’ linear perspective has dominated the study of the morphology of sight since the Renaissance, numerous references to the ‘sphere’ of vision can be found dating back to antiquity. First suggested in Euclid’s Optics<sup>15</sup>, references to the curvature of the visual field has fascinated artists and astronomers alike, appearing in the writings of Johannes Kepler<sup>16</sup>, Leonardo da Vinci<sup>17</sup>, William Hershel<sup>18</sup>, Erwin Panofsky (1924), Ernst Gombrich (1972), and others (Tyler, 2009; Veltman, 1994). Though these observations have been overshadowed by analysis of single-point ‘linear’ perspective, these curvilinear speculations form a tradition that, according to Panofsky (1960), “considered our sphere of vision quite literally as a ‘sphere’” (Figure 12). This assumption, he insists, “more nearly agrees with physiological and psychological reality than that which underlies Brunelleschi's rectilinear construction” (p. 128).}} | ||
| + | |||
| + | Footnotes: | ||
| + | |||
| + | :<sup>15</sup> Kim Veltman (2004, p. 15) reviews the debate concerning the degree to which Euclid’s Optics was a precursor to either linear or spherical perspective in Literature on Perspective: Sources and Literature of Perspective. | ||
| + | |||
| + | :<sup>16</sup> Kepler writes, "But our vision has no surface like that of a painting on which it may look at the picture of the hemisphere but only that surface of the sky above in which it sees comets, and it imagines a sphere by the natural instinct of vision. But if a picture of things is extended in straight lines into a concave sphere, and if our vision is in the center of this, the traces of those things will not be straight lines, but, by Hercules, curved ones" (Galilei, Drake, & O’Malley, 1960, pp. 354–355) | ||
| + | |||
| + | :<sup>17</sup> James Elkins (1988, 1994) summarizes the dispute surrounding da Vinci’s position on the curvature of vision in “Did Leonardo develop a theory of curvilinear perspective?” and The Poetics of Perspective. | ||
| + | |||
| + | :<sup>18</sup> Hershel (1869) writes, "In celestial perspective, every point to which the view is for the moment directed, is equally entitled to be considered as the "centre of the picture," every portion of the surface of the sphere being similarly related to the eye. Moreover, every straight line (supposed to be indefinitely prolonged) is projected into a semicircle of the sphere, that, namely, in which a plane passing through the line and the eye cuts its surface. And every system of parallel straight lines, in whatever direction, is projected into a system of semicircles of the sphere, meeting in two common apexes, or vanishing points, diametrically opposite to each other, one of which corresponds to the vanishing point of parallels in ordinary perspective; the other, in such perspective has no existence” (p.70) | ||
Revision as of 16:30, 3 October 2019
Borrowed from antiquity, a cornerstone to astronomy is the celestial sphere, which describes that the celestial bodies are projected to a sphere or dome around the observer. Astronomers use a spherical coordinate system to describe the sky. Indeed, a spherical celestial sky is often put forward as evidence for a spherical world.
Going much further than it being a mere representation of a universe spread out around us, astronomers also explain that straight lines in space will appear to us as curves -- as great circles on the celestial sphere. The Moon Tilt Illusion, in which the illuminated portion of the Moon often and paradoxically points upwards and away from the Sun, is attributed as an effect caused by the Sun and Moon resting at different angles upon the celestial sphere. The Milky Way, usually thought of as a flat entity viewed from the side, appears as a bending arch in the sky on the celestial sphere. The Sun's path bends and warps on the celestial sphere. So too do shooting stars, meteors, and the aurora curve upon the celestial sphere above us. We are told, essentially, that we observe the heavens as if we were inside of a planetarium, where straight lines become curved on a spherical surface around us.
Why should it be that a straight line in space is warped and curved? If a straight line was receding in distance from our position, at which point would that straight line become curved? The celestial sphere is proposed by conventional astronomy without a mechanism, and with only vague statements that it is natural to observe nature in this way. Actively ignored as a topic of discussion, the warping of lines upon the celestial sphere showcases the weakness and untenability of conventional astronomy.
In contrast to this, the Flat Earth Theory's celestial model directly provides a mechanism for why straight lines appear curved in the sky and for our domed observations.
Description
General Astronomy
The book General Astronomy from WikiBooks says:
“ The stars appear to move together across the sky during the night, rising in the east and setting in the west, as if they are affixed to the inside of a dome. Because of this, many ancient civilizations believed that a dome really did enclose the Earth. Only a few centuries ago astronomers came to realize that the stars are actually very far away, scattered throughout the Milky Way Galaxy, rather than attached to the inside of a vast sphere.
The old idea remains useful, however. The concept of the celestial sphere provides a simple way of thinking about the appearance of the stars from Earth without the complication of a more realistic model of the universe. Working with the celestial sphere offers a convenient way of describing what we see from Earth. When we refer to the celestial sphere, we are imagining that everything we see on the sky is set on the inside of a huge spherical shell that surrounds the Earth. We will use the reference points of the celestial sphere as the basis for several coordinate systems used to place celestial locations with respect to one another and to us. ”
University of Virginia
An astronomy course at the University of Virginia describes:
“ Everything appears to move around us as though we were at the center of the Universe. The Celestial Sphere is an imaginary concept that is a useful tool for understanding some workings of the sky:
- - Sphere of infinite radius with Earth at center.
- - Stars on "surface of sphere".
~
Even though we now know that this ancient model of a stationary Earth surrounded by a rotating sphere of stars is incorrect, we still use this model because it is a convenient way to predict the motions of the stars and planets relative to a location on the Earth. ”
New Jersey Institute of Technology
The New Jersey Institute of Technology states:
“ Think of the sky as painted, or projected, onto the inside of a dome--like a planetarium dome. ”
On the Evolution of the Heavenly Spheres
A doctoral thesis explains that the the transformation of straight lines into curves on the celestial sphere has been known since antiquity.
On the Evolution of the Heavenly Spheres
An Enactive Approach to Cosmography
by David McConville
p.40
“ Though analysis of ‘one-point’ linear perspective has dominated the study of the morphology of sight since the Renaissance, numerous references to the ‘sphere’ of vision can be found dating back to antiquity. First suggested in Euclid’s Optics15, references to the curvature of the visual field has fascinated artists and astronomers alike, appearing in the writings of Johannes Kepler16, Leonardo da Vinci17, William Hershel18, Erwin Panofsky (1924), Ernst Gombrich (1972), and others (Tyler, 2009; Veltman, 1994). Though these observations have been overshadowed by analysis of single-point ‘linear’ perspective, these curvilinear speculations form a tradition that, according to Panofsky (1960), “considered our sphere of vision quite literally as a ‘sphere’” (Figure 12). This assumption, he insists, “more nearly agrees with physiological and psychological reality than that which underlies Brunelleschi's rectilinear construction” (p. 128). ”
Footnotes:
- 15 Kim Veltman (2004, p. 15) reviews the debate concerning the degree to which Euclid’s Optics was a precursor to either linear or spherical perspective in Literature on Perspective: Sources and Literature of Perspective.
- 16 Kepler writes, "But our vision has no surface like that of a painting on which it may look at the picture of the hemisphere but only that surface of the sky above in which it sees comets, and it imagines a sphere by the natural instinct of vision. But if a picture of things is extended in straight lines into a concave sphere, and if our vision is in the center of this, the traces of those things will not be straight lines, but, by Hercules, curved ones" (Galilei, Drake, & O’Malley, 1960, pp. 354–355)
- 17 James Elkins (1988, 1994) summarizes the dispute surrounding da Vinci’s position on the curvature of vision in “Did Leonardo develop a theory of curvilinear perspective?” and The Poetics of Perspective.
- 18 Hershel (1869) writes, "In celestial perspective, every point to which the view is for the moment directed, is equally entitled to be considered as the "centre of the picture," every portion of the surface of the sphere being similarly related to the eye. Moreover, every straight line (supposed to be indefinitely prolonged) is projected into a semicircle of the sphere, that, namely, in which a plane passing through the line and the eye cuts its surface. And every system of parallel straight lines, in whatever direction, is projected into a system of semicircles of the sphere, meeting in two common apexes, or vanishing points, diametrically opposite to each other, one of which corresponds to the vanishing point of parallels in ordinary perspective; the other, in such perspective has no existence” (p.70)