Celestial Sphere

Borrowed from antiquity, a cornerstone to astronomy is the celestial sphere, which describes that the celestial bodies are projected to a sphere or dome around the observer. Astronomers use a spherical coordinate system to describe the sky. A spherical celestial sky is often put forward as evidence for a spherical world.

Reading closer, the celestial sphere goes much further than it being a mere representation of a universe spread out around us. Astronomers also explain that straight lines in space will appear to us as curves on the celestial sphere. The Moon Tilt Illusion, in which the illuminated portion of the Moon often and paradoxically points upwards and away from the Sun, is attributed as an effect caused by the Sun and Moon resting at different angles upon the celestial sphere. The Milky Way, usually thought of as a flat entity viewed from the side, appears as a bending arch in the sky on the celestial sphere. The Sun's path bends and warps on the celestial sphere. So too do shooting stars, meteors, and the aurora curve upon the celestial sphere above us. We are told, essentially, that we observe the heavens as if we were inside of a planetarium, where straight lines become curved on a spherical surface around us.

Why should it be that a straight line in space is warped and curved? If a straight line was receding in distance from our position, at which point would that straight line become curved? The celestial sphere is proposed by conventional astronomy without a mechanism, and with only vague statements that it is natural to observe nature in this way. Actively ignored as a topic of discussion, neglected in astronomy texts, and mainly trotted out when forced to explain phenomena, the warping of lines upon the celestial sphere showcases the weakness and untenability of conventional astronomy.

In contrast to this, the Flat Earth Theory's celestial model directly provides a mechanism for why lines, containing points at different distances from the observer, appear curved in the sky and for our domed observations.

Description

General Astronomy

The book General Astronomy (Archive) from WikiBooks says:

  “ The stars appear to move together across the sky during the night, rising in the east and setting in the west, as if they are affixed to the inside of a dome. Because of this, many ancient civilizations believed that a dome really did enclose the Earth. Only a few centuries ago astronomers came to realize that the stars are actually very far away, scattered throughout the Milky Way Galaxy, rather than attached to the inside of a vast sphere.

The old idea remains useful, however. The concept of the celestial sphere provides a simple way of thinking about the appearance of the stars from Earth without the complication of a more realistic model of the universe. Working with the celestial sphere offers a convenient way of describing what we see from Earth. When we refer to the celestial sphere, we are imagining that everything we see on the sky is set on the inside of a huge spherical shell that surrounds the Earth. We will use the reference points of the celestial sphere as the basis for several coordinate systems used to place celestial locations with respect to one another and to us. ”

University of Virginia

An astronomy course at the University of Virginia describes (Archive):

  “ Everything appears to move around us as though we were at the center of the Universe. The Celestial Sphere is an imaginary concept that is a useful tool for understanding some workings of the sky. ...Even though we now know that this ancient model of a stationary Earth surrounded by a rotating sphere of stars is incorrect, we still use this model because it is a convenient way to predict the motions of the stars and planets relative to a location on the Earth. ”

New Jersey Institute of Technology

The New Jersey Institute of Technology states (Archive):

  “ Think of the sky as painted, or projected, onto the inside of a dome--like a planetarium dome. ”

Princeton University

Professor of Astronomy Charles A.Young, Ph.D, defines spherical astronomy as (Archive):

“ Spherical Astronomy — This, discarding all consideration of absolute dimensions and distances, treats the heavenly bodies simply as objects moving on the “surface of the celestial sphere”: it has to do only with angles and directions, and, strictly regarded, is in fact merely Spherical Trigonometry applied to Astronomy. ”

On the Evolution of the Heavenly Spheres

A doctoral thesis explains that the the transformation of straight lines into curves on the celestial sphere has been known since antiquity.

On the Evolution of the Heavenly Spheres
An Enactive Approach to Cosmography
by David McConville

Full Text Link (Archive)

p.40

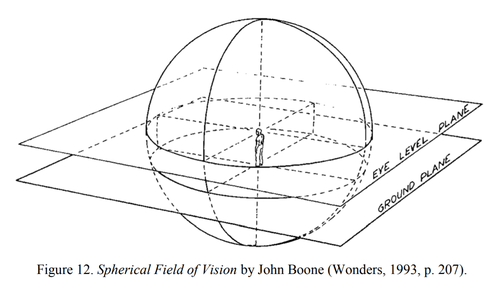
  “ Though analysis of ‘one-point’ linear perspective has dominated the study of the morphology of sight since the Renaissance, numerous references to the ‘sphere’ of vision can be found dating back to antiquity. First suggested in Euclid’s Optics¹⁵, references to the curvature of the visual field has fascinated artists and astronomers alike, appearing in the writings of Johannes Kepler¹⁶, Leonardo da Vinci¹⁷, William Hershel¹⁸, Erwin Panofsky (1924), Ernst Gombrich (1972), and others (Tyler, 2009; Veltman, 1994). Though these observations have been overshadowed by analysis of single-point ‘linear’ perspective, these curvilinear speculations form a tradition that, according to Panofsky (1960), “considered our sphere of vision quite literally as a ‘sphere’” (Figure 12). This assumption, he insists, “more nearly agrees with physiological and psychological reality than that which underlies Brunelleschi's rectilinear construction” (p. 128). ”

Footnotes:

¹⁵ Kim Veltman (2004, p. 15) reviews the debate concerning the degree to which Euclid’s Optics was a precursor to either linear or spherical perspective in Literature on Perspective: Sources and Literature of Perspective.

¹⁶ Kepler writes, "But our vision has no surface like that of a painting on which it may look at the picture of the hemisphere but only that surface of the sky above in which it sees comets, and it imagines a sphere by the natural instinct of vision. But if a picture of things is extended in straight lines into a concave sphere, and if our vision is in the center of this, the traces of those things will not be straight lines, but, by Hercules, curved ones" (Galilei, Drake, & O’Malley, 1960, pp. 354–355)

¹⁷ James Elkins (1988, 1994) summarizes the dispute surrounding da Vinci’s position on the curvature of vision in “Did Leonardo develop a theory of curvilinear perspective?” and The Poetics of Perspective.

¹⁸ Hershel (1869) writes, "In celestial perspective, every point to which the view is for the moment directed, is equally entitled to be considered as the "centre of the picture," every portion of the surface of the sphere being similarly related to the eye. Moreover, every straight line (supposed to be indefinitely prolonged) is projected into a semicircle of the sphere, that, namely, in which a plane passing through the line and the eye cuts its surface. And every system of parallel straight lines, in whatever direction, is projected into a system of semicircles of the sphere, meeting in two common apexes, or vanishing points, diametrically opposite to each other, one of which corresponds to the vanishing point of parallels in ordinary perspective; the other, in such perspective has no existence” (p.70)

Sun Path Warped

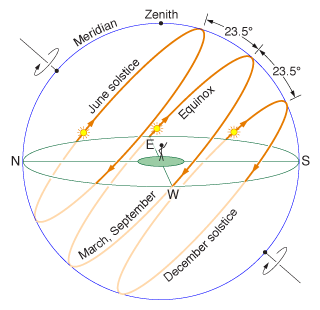
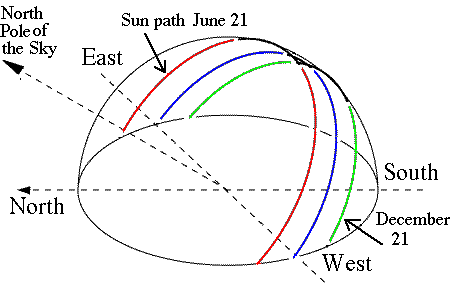
According to the conventional model the sun's path is a plane which intersects the observer's sky.

• 

  Seasonal Sun Path - Weber University

• 

  Sun Path diagram from NASA.gov

• 

  Plane of the Sun from Kutztown University

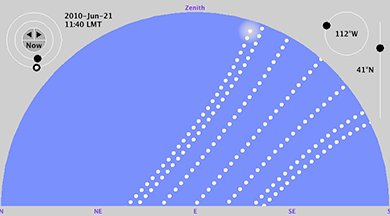
A Weber State University astronomy course by Dr. Daniel V. Schroeder (bio) shows the Sun's path is warped upon the celestial dome:

https://physics.weber.edu/schroeder/ua/sunandseasons.html (Archive)

Caption:   “ This simulated multiple-exposure image shows the path of the rising sun through the eastern sky on the morning of the 21st of each month, from December at the right through June at the left. The latitude was set to 41° north. (The spreading of the trails as they go upward is a distortion caused by stretching the domed sky onto a flat semicircle.) ”

The above website explains the distortion as caused by 'stretching the domed sky onto a flat semicircle' -- as if there is a domed sky around us which modifies the position of the Sun. The diagram comes from the linked Sky Motion Applet.

Dr. Schroeder also provides the following multiple-exposure photo:

  “ Multiple-exposure photo of the setting sun, showing that it follows the same diagonal path that a star would, as seen from a mid-northern latitude. This photo was made on June 21, when the sun set considerably north of due west. ”

Moon and Venus Star Trails

Like the Sun on the celestial dome, Venus and the Moon can also be seen to follow the path of the stars.

"Crescent Moon Venus and star trails at Nagano, Norikura mountain" (Source)

Milky Way Arch

As with the ecliptic, the Milky Way is thought to be a straight entity which we are viewing from the side. It has been asserted that the Milky Way is seen as an arch in the sky.

Source: Matt Rohlader Photography | Caption: "The arch of the Milky Way as seen from Split Rock Lighthouse State Park near Two Harbors, MN."

A Google Image Search for 'Milky Way Arch' will provide many images of the Milky Way arching in the sky.

Photographs of the Milky Way Arch from Google Image Search have been described as being affected by wide-angle, fish-eye, panorama, or other effects. While true that many images of the Milky Way Arch are affected by such distortion, sources tell us that the arch can be seen with the naked eye as well. Astronomer and Associate Editor Alison Klesman, Ph.D. (bio), at Astronomy Magazine informs us that both the Milky Way and the ecliptic (the planar path of the Sun) project as a great circle onto the celestial sphere, which create straight lines overhead, and at lower altitudes create arcs in the sky which are visible to the naked eye:

http://www.astronomy.com/magazine/ask-astro/2018/09/seeing-a-curved-milky-way (Archive)

  “ The Milky Way appears straightest when it is most directly overhead. Astronomy senior editor Rich Talcott points out, “The plane of the Milky Way projects as a great circle onto the celestial sphere (as does the ecliptic, which we are also in). So both the Milky Way and the ecliptic appear as large circles in the sky (which, if they happen to pass overhead, will appear as straight lines). But if the circles reach a peak altitude of only, say, 30°, they’re going to look like arcs to the naked eye." ”

Meteors

The International Meteor Organization says (Archive)

  “ As we mentioned earlier, meteors describe arcs on the celestial sphere that are parts of great circles. Such a circle determines a plane. Plotting a meteor then comes down to determining the intersection between this plane and the plane on which the stars were projected. Figure 1 shows two meteors and their great circles on the celestial sphere. ”

http://www.internetsv.info/MeteorRC.html (Archive)

  “ As seen from a point on the Earth's surface, meteor trails will appear to be following great circle paths. The great circles for meteors of a shower have two common intersection points; the radiant above the horizon and the anti-radiant below. The geometric definition of a great circle is the intersection of the sphere and a plane that passes through the center of the sphere. ”

Aurora

Astronomer and mathematician Simon Newcomb (bio) tells us in his Popular Astronomy that the aurora, too, projects upon the celestial sphere (Archive):

p.309

  “ A close study of the aurora indicates that its connection is not with the geographical, but with the magnetic pole. Two distinct kinds of light are seen in the aurora; or we might say that the light assumes two distinct forms, of which’ some- times the one aud sometimes the other preponderates. They are as follows:

~

2. The streamer or pillar form. This form consists of long streamers or pillars, which extend in the direction of the dipping magnetic needle. They look curved or arched, like the celestial sphere on which they are projected, but they are really straight. They are in a state of constant motion. Sometimes they are spread out in the form of an immense flag with numerous folds, dancing, quivering, and undulating, as if moved by the wind. ”

Moon Tilt Illusion

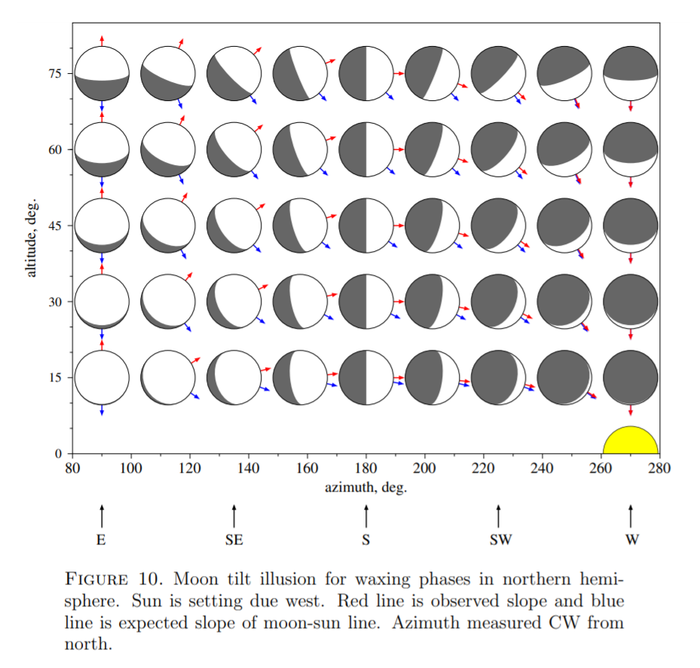
If the Moon is illuminated by the Sun then it is expected that the illuminated portion of the Moon will point at it. The Moon Tilt Illusion is a geometric anomaly in which the Moon is often seen to point upwards and away from the Sun. Astronomers attribute this to the Sun and Moon resting at different angles on the 'celestial sphere'.

Professor Alan Myers at the University of Pennsylvania says the following (Archive):

  “ Astronomers rely upon the celestial sphere model for maps of the sky because locations of stars and constellations depend only on their right ascension and declination. For the topocentric model used for the sun and the moon, location is specified by azimuth and altitude. All objects in the sky are assumed to be located at the same distance from the observer, as if pasted upon the surface of an imaginery sphere surrounding the observer. Astronomers, for whom the celestial sphere model is a basic tool for mapping the stars, are not surprised by the apparently curved path of light from the sun to the moon because they know that straight lines in 3-D object space are transformed to great-circle arcs on the imaginary celestial sphere. ”

A diagram is provided:

Professor Myers informs us on the interest of astronomers to discuss this topic:

  “ The moon tilt illusion is not described in astronomy textbooks because astronomers know that straight lines in object space become great circles on the celestial sphere. ”

MetaBunk

A physics educator under the alias Henk001 was kind enough to take the time to provide us with a free science lecture on the workings of astronomy, instructing us with the following(Archive):

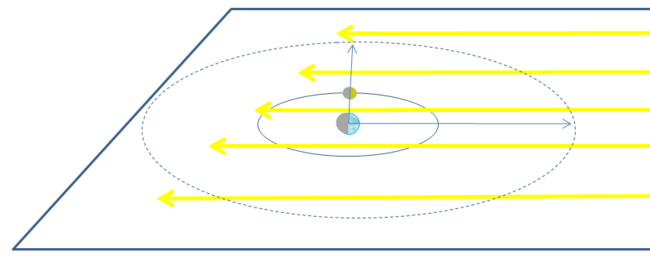
  “ I had a night to sleep on it and I came up with this short lecture (I am a physics teacher so you will excuse me for being a bit excessive). First, to put things in perpective, a scale drawing of the earth, moon and the moon's orbit....

~

We now are trying to see the moon's orbit in perspective, putting it in a plane and let the sunlight come from the right. Also we blow up the size of the earth and the moon:

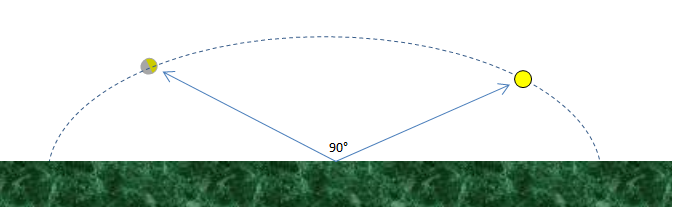
Now look at the two blue arrows, representing the viewing directions towards the moon and towards the sun, they make an angle of 90°. The dashed circle is an arbitrary circle on which we see both the moon and the sun. Now what does this circle look like when projected on the celestial sphere -- which is, for clarity, an imaginary "sphere of directions"?

~

from the standpoint of an observer living in the mid latitudes:

remember that these 2-dimensional pictures are projections of a 3-dimensional viewing sphere. At the equator the moon will even look like this:

So, on the celestial "sphere" you have to imagine a great circle, being the section of the earth-moon-sun-plane with that sphere. The circle is tilted more or less depending on your latitude (for the sake of simplicity again I also ignore the tilt of the earth's axis and the inclination of the moon's orbit), causing this illusion. ”

The educator explains that a 'celestial sphere' modifies the directions of the sun and moon, causing the illuminated portion of to Moon to point in a different direction. Following this enlightenment, our expert continues:

  “ And that is essentially where flat earthers go wrong. Their INTERPRETATION of what they observe doesn't match the generally accepted model, "so the model must be wrong" -- instead of "so what am I overlooking?" (and ask an expert (site) to explain). ”

We are told by a molder of young minds that when something does not make sense about the world our intuition and correct course of action should be to surrender curiosity, criticism, and all sense of geometry. Instead, we must seek to "ask an expert"—stoic educators and pillars of the community who will proceed to correct our misunderstanding of nature with impeachable facts from science scholarship, such as with teachings of the celestial dome which the celestial bodies project upon at different angles and where straight lines become curved.

Sky Dome and Projections

Over the course of the year the path of the Sun is seen to curve upon a dome, which can be seen in sun charts. Penn State University provides an overview of 'sky domes', projections, and polar sun charts:

https://www.e-education.psu.edu/eme810/node/534 (Archive)

2.13 Sky Dome and Projections
Sun Charts: Projections of Solar Events and Shadowing from the Sky Dome

  “ The emphasis of this lesson is the Sun Chart tool (or Sun Path). These flat diagrams are found in many solar design tools, but may look completely foreign to the new student in solar energy. How do we interpret the arcs and points plotted on a sun chart? Why do we have two different types of plots (one looks like a rectangle, and one looks like a circle)? Why do some plots go from 0-360°, while others go from -180° to +180°?

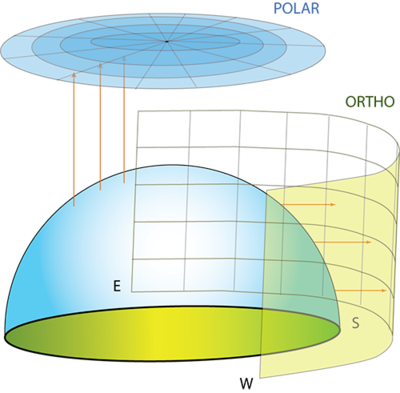
If we want to visually convert our observations of the sky-dome onto a two-dimensional medium, we can either use an orthographic projection or a spherical projection on a polar chart. These projections are useful for calculating established times of solar availability or shadowing for a given point of solar collection. ...The Sky Dome refers to the sum of the components for the entire sky from horizon to zenith, and in all azimuthal directions.

~

Projections

The sky dome can be projected onto flat surfaces for analysis of shading and sky component behavior.

Figure 2.15: The sky dome as projected to the right in orthographic form, and as projected upward in polar form.

~

Polar Projection: takes the sky dome and projects altitude and azimuth values down onto a circular plane. However, in the polar projection, the arc for December 21 is at the top while the arc for June 21 is at the bottom. This happens because we are effectively lying on the ground with our heads facing south, and holding that large piece of paper straight up to the sky.

Figure 2.17: Polar Projection ”

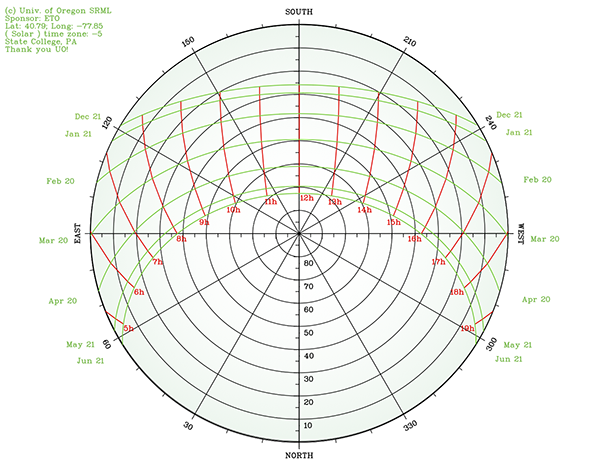
The above is a polar sun chart, showing how the sun would move as if we were laying on the ground with our head towards the south. Holding a large piece of paper straight up into the air, over the course of the year the sun would shine through the paper and trace arcs across the sky. Despite the sun's ecliptic being a plane which cuts through the earth, the path of the sun is seen to curve in the sky.

At the bottom of the page we see that the polar projection sun chart was generated with the University of Oregon's Polar Sun Chart Program. Using this tool to create a polar sun chart for the opposite Southern Hemisphere version of the above polar sun chart, for Latitude -40.79 and Longitude -77.85, we see the following:

Notice that the day of December 21st is convex in the Northern Hemisphere and concave in the Southern Hemisphere. The shape of the curve for the same day is seen to be convex and concave for different observers simultaneously, truly as if each observer had his or her own personal planitarium-like "dome" of vision.

Addendum

The 'celestial sphere' is seen to be quite literal. Distant observations paradoxically project upon a sphere around the observer. In order for different observers to have his or her own personal dome where lines simultaneously appear concave and convex depending on position, the mechanism cannot be anything other than the curvature of light rays creating the appearance of our domed surroundings, and hence a piece of evidence for the Flat Earth's celestial model of Electromagnetic Acceleration.

See Also

• Moon Tilt Illusion
• Electromagnetic Acceleration