Variations in Gravity

The Variations in Gravity are the supposed variations to gravity due to either the variations in strength of the gravitational field of the earth or due to the presence of masses such as hills or celestial bodies. It is often stated that the strength of gravity decreases with altitude or that the gravity of the Sun and Moon pulls upon the earth's surface.

A number of tests have been conducted in search of these variations. It has been found that in experiments on medium and long ranges, "gravity" does not deviate from the Universality of Free Fall or the Equivalence Principle. The Equivalence Principle is a principle of nature which says that 'gravity' behaves as if the experiment were conducted on an Earth or in a container which was accelerating upwards. Supposedly only a 'local' concept, experimenters have tested this concept at various vertical distances without violation of this principle.

External gravity sources, such as from the Sun, are also unable be felt. Gravity appears to behave as if the earth is accelerating upwards, that the strength of gravity is uniform, and there are no other gravitating sources around us.

Also see Weight Variation by Latitude for discussion on the weight variation by latitude experiments.

Celestial Variations in G

The Equivalence Principle Torsion Balance tests are incredibly reliable precision machines which are used to measure the Equivalence Principal to increasing sensitivity. Experimenters have redesigned the Equivalence Principle's Torsion Balance tests to try and detect the gravity variations caused by the sun, moon, and the tidal forces. It was found that the gravitational influence of the sun, moon, or the tidal forces could not be measured as manifest of the attraction of the bodies in the experiments. Variations to "gravity" did not appear.

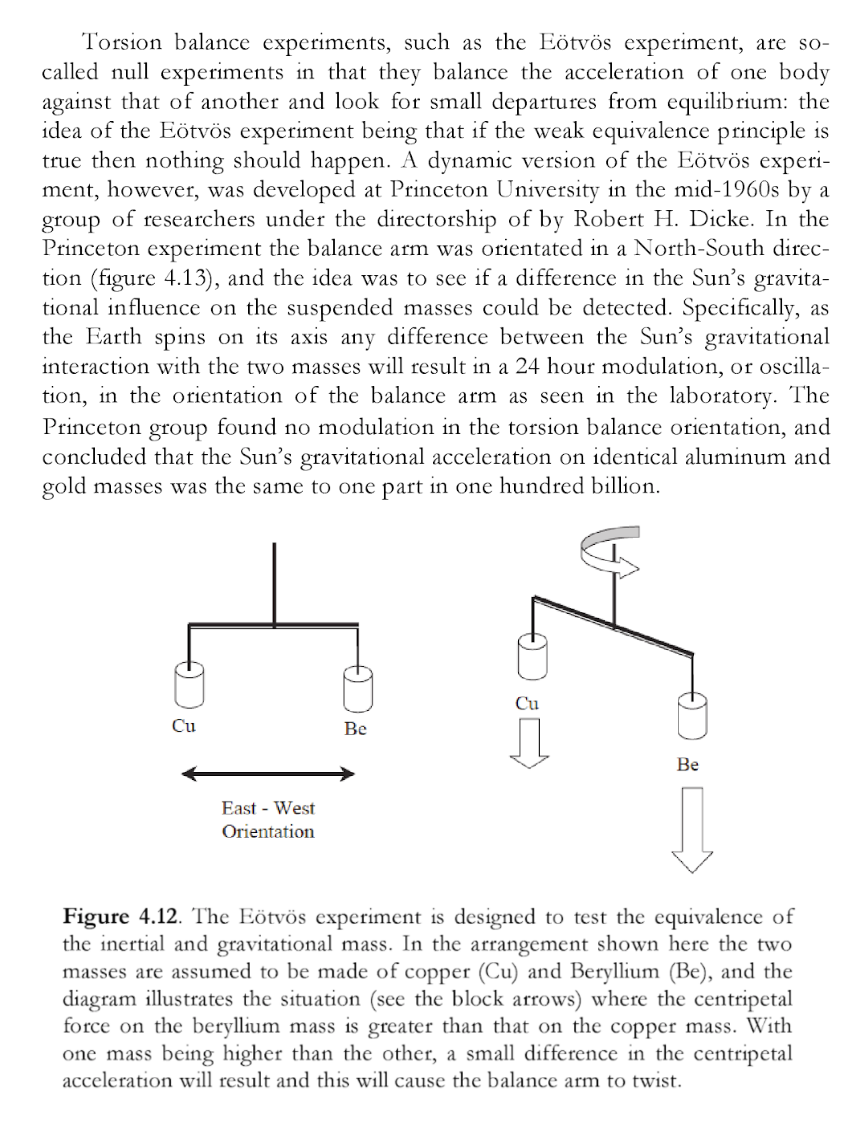
Princeton Experiment

From 'The Pendulum Paradigm: Variations on a Theme and the Measure of Heaven and Earth', by Professor Martin Beech, we read the following on p.176:

Essentially, the experiment is summarized as follows:

“ In the Princeton experiment the balance arm was oriented in a North-South direction (figure 4.13), and the idea was to see if a difference in the Sun's gravitational influence on the suspended masses could be detected. Specifically, as the Earth spins on its axis and difference between the Sun's gravitational interaction with the two masses will result in a 24 hour modulation or oscillation, in the orientation of the balance arm as seen in the laboratory. The Princeton group found no modulation of the torsion balance, and concluded that the Sun's gravitational acceleration on identical aluminum and gold masses was the same to one part in one hundred billion. ”

The masses were not attracted to the sun in the experiment, to an accuracy of one part in one hundred billion.

Moscow State University Experiment

The experiment was repeated and improved by researchers at Moscow State University. The title of the paper states the conclusion:

Verification of the Equivalence of Inertial and Gravitational Mass
V. B. Branginsky and V. I. Panov
Full Text Link (Archive)

“ During the period 1959-1964 the principle of equivalence was again tested by Dicke, Krotkov, and Roll. [2] A hypothetical difference between the accelerations of two bodies, made of gold and aluminum, respectively, in the gravitational field of the sun was measured. From measurements conducted during many months it was concluded that the ratio of the inertial and gravitational masses for these two bodies does not differ by more than 3 x 10^-11 with 95% confidence.[2] An analysis of the experimental work in [2] shows that it is possible, in principle, to considerably improve the resolution by using a mechanical oscillatory system having a long relaxation time.[3] We shall here describe an experiment intended as a new test of the principle of equivalence.

1. MEASUREMENT TECHNIQUE

We retained the experimental scheme of Dicke, Krotkov, and Roll. [2] A torsion balance falling together with the earth in the gravitational field of the sun should be acted upon by a torsional mechanical moment that is proportional to a hypothetical difference between the accelerations of the materials comprising the balance (if the principle of equivalence is not fulfilled). Because of the earth's rotation this moment should vary sinusoidally with a 24-hour period (Fig. 1). ”

Repetitions

Additional experiments of this class are described (Archive). The first two experiments in this list are the Princeton and Moscow State experiments above:

Authors	Year	Description	Accuracy
Roll, Krotkov and Dicke	1964	Torsion balance experiment, dropping aluminum and gold test masses	difference is less than one part in one hundred billion
Branginsky and Panov	1971	Torsion balance, aluminum and platinum test masses, measuring acceleration towards the sun	difference is less than 1 part in a trillion (most accurate to date)
Eöt-Wash	1987–	Torsion balance, measuring acceleration of different masses towards the earth, sun and galactic center, using several different kinds of masses	difference is less than a few parts in a trillion

The Eöt-Wash experiments were repeated by others:

https://plato.stanford.edu/entries/physics-experiment/app4.html (Archive)

“ The torsion-balance experiments of Eöt-Wash were repeated by others including (Cowsik et al. 1988; Fitch, Isaila and Palmer 1988; Adelberger 1989; Bennett 1989; Newman, Graham and Nelson 1989; Stubbs et al. 1989; Cowsik et al. 1990; Nelson, Graham and Newman 1990). These repetitions, in different locations and using different substances, gave consistently negative results. ”

Long Range Variations in G

Universality of Free Fall

The Newtonian gravitational constant: recent measurements and related studies
By George T Gillies

Full Text Link (Archive)

p.200

5. Searches for variations in G
5.1. Spatial dependence of G

“ Searches for a change in G with intermass spacing have constituted a compelling quest in laboratory gravitation, especially during the past 25 years. The motivations for carrying out this kind of study were originally empirical, with the results of various benchtop experiments being interpreted in terms of either a value for or limit on some distance-dependent form of the gravitational constant (i.e. a G(r) effect), or in terms of a breakdown in the inverse square law (i.e. a modification to it of the form 1/r^2+δ, where δ is the departure parameter). Then, in the 1980s, observations that seemingly revealed evidence for non-Newtonian gravity at larger distance scales (Stacey et al 1987) fuelled much additional interest in this line of work. The contemporaneous suggestion by Fischbach et al (1986) that there may be previously undiscovered, weak, long-range forces in nature provided further impetus for investigating the composition- and distance-dependence of gravity, since the presence of any such effect might reveal the existence of a new force. During this time, a theoretical framework for admitting non-Newtonian effects into discussions of the experimental results was emerging. It led to the practice of using the laboratory data to set limits on the size of the strength-range parameters in a Yukawa term added onto the Newtonian potential, and this has become a standard method for intercomparing the results of this class of experiments. Even though convincing evidence in favour of such new weak forces was never found, the many resulting experiments, when viewed as tests of the universality of free-fall, did much to improve the experimental underpinnings of the weak equivalence principle (WEP) of general relativity. In fact, searches for departures from the inverse square behaviour of Newtonian gravity have now come to be interpreted as attempts to uncover violations of the WEP. ”

The above says that searches for departures from the inverse square bahavior of Newtonian gravity would be a violation of the Equivalence Principle which says that gravity is indistinguishable from an experiment which takes place on an upwardly accelerating Earth or compartment.

p.202

“ Other recent experimental searches for a breakdown in Newtonian gravity at large distances include a second set of tower gravity measurements made by Romaides et al (1994). Their data, taken at five points over a nearly 500m vertical rise, reconfirmed the exactness of the inverse square law. A similar result over a vertical distance of approximately 320 m was obtained at a meteorological tower in China by Liu et al (1992). ”

It should be noted that 500 meters is 1640.42 feet, and about as high as the Shanghai World Financial Center, a skyscraper in China.

Inverse Squared Law

The 'inverse squared law', the 'Universality of Free Fall,' and the 'Weak Equivalence Principle' refers to the 9.8 meters per second squared rate of acceleration. From Foundations of Modern Cosmology we see a description of the inverse square law and how Newton interpreted the phenomenon in coming up with his theory of gravity:

“ In MKS units, the acceleration due to gravity at the surface of the earth is 9.8 meters per second per second, or 9.8 m s^-2. That is, if an object falls from rest, and air resistance can be neglected, at the end of one second is will be traveling 9.8 meters per second; at the end of another second it will attain the speed of 19.6 meters per second; and so fourth, until it hits the ground or air resistance balances the force due to gravity.

Once Newton had determined that gravity followed an inverse square force law, he was able to prove that Kepler's first and second laws followed necessarily. ”

Medium Range Variations in G

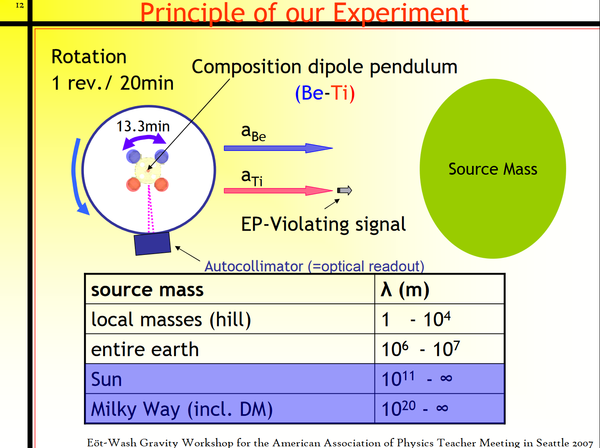
Eöt-Wash Hill Experiments

From No Easy Answers: Science and the Pursuit of Knowledge by Professor Allan Franklin (bio), on p.70 we read a summary of the Eöt-Wash hillside experiments with the rotating torsion balance:

“ The Eöt-Wash experiment used a torsion pendulum located on the side of a hill on the University of Washington campus. If the hill attracted the copper and beryllium test bodies that were used in the apparatus differently, then the torsion balance would experience a net torque. None was observed. ”

Study Link

An Eöt-Wash presentation explains (Archive) that the influence of an external source mass on these type of experiments would be a violation of the Equivalence Principle (EP).

One will notice from the graphic above that any horizontal pulling phenomenon would violate the Equivalence Principle which states that gravity operates exactly like a rocket ship accelerating upwards at 1G with no other gravitating bodies around.

Short Range Variations in G

Over shorter ranges, such as with the Cavendish Experiment, it has been seen that an attraction was found, but the attraction is not consistent. The strength of "gravity" in the universe changes by over ten fold when tested at different times. This inconsistency suggests that there are other more dominant effects at that range creating or modifying those results and that the experiment has not yet been properly refined to remove all sources of error.

On the topic of the Cavendish Experiment, the Encyclopedia Britannica article discussed below says:

“ However, despite the great attention given to systematic errors in those experiments, it is clear from the range of the results that serious discrepancies, much greater than the apparent random errors, still afflict determinations of G. ”

For further information see the Cavendish Experiment

Encyclopedia Britannica

Encyclopedia Britannica has provided an article on the experimental study of gravity. Aside from the gravimeter devices which have been shown to be seismometers (See: Gravimetry) and the Cavendish Experiment, which is an inconsistent short range experiment, Encyclopedia Britannica agrees that there are no variations in gravity:

https://www.britannica.com/science/gravity-physics/Experimental-study-of-gravitation (Archive)

“ Early in the 1970s an experiment by the American physicist Daniel R. Long seemed to show a deviation from the inverse square law at a range of about 0.1 metre. Long compared the maximum attractions of two rings upon a test mass hung from the arm of a torsion balance. The maximum attraction of a ring occurs at a particular point on the axis and is determined by the mass and dimensions of the ring. If the ring is moved until the force on the test mass is greatest, the distance between the test mass and the ring is not needed. Two later experiments over the same range showed no deviation from the inverse square law. In one, conducted by the American physicist Riley Newman and his colleagues, a test mass hung on a torsion balance was moved around in a long hollow cylinder. The cylinder approximates a complete gravitational enclosure and, allowing for a small correction because it is open at the ends, the force on the test mass should not depend on its location within the cylinder. No deviation from the inverse square law was found. In the other experiment, performed in Cambridge, Eng., by Y.T. Chen and associates, the attractions of two solid cylinders of different mass were balanced against a third cylinder so that only the separations of the cylinders had to be known; it was not necessary to know the distances of any from a test mass. Again no deviation of more than one part in 10⁴ from the inverse square law was found. Other, somewhat less-sensitive experiments at ranges up to one metre or so also have failed to establish any greater deviation.

The geophysical tests go back to a method for the determination of the constant of gravitation that had been used in the 19th century, especially by the British astronomer Sir George Airy. Suppose the value of gravity g is measured at the top and bottom of a horizontal slab of rock of thickness t and density d. The values for the top and bottom will be different for two reasons. First, the top of the slab is t farther from the centre of Earth, and so the measured value of gravity will be less by 2(t/R)g, where R is the radius of Earth. Second, the slab itself attracts objects above and below it toward its centre; the difference between the downward and upward attractions of the slab is 4πGtd. Thus, a value of G may be estimated. Frank D. Stacey and his colleagues in Australia made such measurements at the top and bottom of deep mine shafts and claimed that there may be a real difference between their value of G and the best value from laboratory experiments. The difficulties lie in obtaining reliable samples of the density and in taking account of varying densities at greater depths. Similar uncertainties appear to have afflicted measurements in a deep bore hole in the Greenland ice sheet.

New measurements have failed to detect any deviation from the inverse square law. The most thorough investigation was carried out from a high tower in Colorado. Measurements were made with a gravimeter at different heights and coupled with an extensive survey of gravity around the base of the tower. Any variations of gravity over the surface that would give rise to variations up the height of the tower were estimated with great care. Allowance was also made for deflections of the tower and for the accelerations of its motions. The final result was that no deviation from the inverse square law could be found.

...Thus far, all of the most reliable experiments and observations reveal no deviation from the inverse square law. ”

Torsion Balances

On the topic of the Torsion Balance tests discussed above which attempted to measure the gravitation of the sun, Encyclopedia Britannica says:

“ Experiments with ordinary pendulums test the principle of equivalence to no better than about one part in 10⁵. Eötvös obtained much better discrimination with a torsion balance. His tests depended on comparing gravitational forces with inertial forces for masses of different composition. Eötvös set up a torsion balance to compare, for each of two masses, the gravitational attraction of Earth with the inertial forces due to the rotation of Earth about its polar axis. His arrangement of the masses was not optimal, and he did not have the sensitive electronic means of control and reading that are now available. Nonetheless, Eötvös found that the weak equivalence principle (see above Gravitational fields and the theory of general relativity) was satisfied to within one part in 10⁹ for a number of very different chemicals, some of which were quite exotic. His results were later confirmed by the Hungarian physicist János Renner. Renner’s work has been analyzed recently in great detail because of the suggestion that it could provide evidence for a new force. It seems that the uncertainties of the experiments hardly allow such analyses.

Eötvös also suggested that the attraction of the Sun upon test masses could be compared with the inertial forces of Earth’s orbital motion about the Sun. He performed some experiments, verifying equivalence with an accuracy similar to that which he had obtained with his terrestrial experiments. The solar scheme has substantial experimental advantages, and the American physicist Robert H. Dicke and his colleagues, in a careful series of observations in the 1960s (employing up-to-date methods of servo control and observation), found that the weak equivalence principle held to about one part in 10¹¹ for the attraction of the Sun on gold and aluminum. A later experiment by the Russian researcher Vladimir Braginski, with very different experimental arrangements, gave a limit of about one part in 10¹² for platinum and aluminum.

Galileo’s supposed experiment of dropping objects from the Leaning Tower of Pisa has been reproduced in the laboratory with apparatuses used to determine the absolute value of gravity by timing a falling body. Two objects, one of uranium, the other of copper, were timed as they fell. No difference was detected. ”

Conclusion

The Britannica article concludes:

“ By the start of the 21st century, all observations and experiments on gravitation had detected that there are no deviations from the deductions of general relativity, that the weak principle of equivalence is valid, and that the inverse square law holds over distances from a few centimetres to thousands of kilometres. ”

Searching for Extra Dimensions

From the introduction of Searching for Extra Dimensions and New String-Inspired Forces in the Casimir Regime (Archive), its authors Dr. Dennis E. Krause (bio) and Professor Ephraim Fischbach (bio) tell us:

“ When Isaac Newton formulated his law of universal gravity over 300 years ago, he provided the first mathematical description of one of the fundamental forces of nature. Yet, physicists have realized only relatively recently that tests of Newtonian gravity can still provide a unique window into new physics [1-7]. Within the past 20 years, experimentalists have put Newtonian gravity to the test for distance scales 10^-3-10¹⁵ m by searching for violations of the weak equivalence principle (WEP) and inverse square law (ISL). The fact that no such violations have been observed places stringent constraints on extensions of the Standard Model that would naturally lead to such effects [1]. ”

The Weak Equivalence Principle is the principle of nature which states that the gravity behaves as if the observer were on a surface which was accelerating upwards. The Inverse Squared Law is the law which says that bodies will fall at inverse proportion to the square of the distance from the Earth. The above states that experimentalists have searched for violations in the WEP and the Inverse Squared Law on ranges from 10^-3 m to 10¹⁵ m and that "no such violations have been observed".

History of the Torsion Balance

The history of the Torsion Balance experiments began in 1889, with Barron Rosland von Eötvös' attempt to detect the Coriolis force.

Foundations of Modern Cosmology
By Professor John F. Hawley, and Katherine A. Holcomb

From p.219 of the above text we read:

“ The first highly accurate experiment to test the equivalence principle was performed in 1889 by Barron Rosland von Eötvös. Eötvös constructed a device called a torsion balance. He suspended two bodies of nearly equal mass but different composition, from a beam which hung from a very fine wire precisely at its center. If the magnitudes of the Coriolis force (from the Earth's rotation) and the gravitational force had differed between the bodies due to their differing composition, Eötvös would have been able to detect a twisting of the wire. None was seen, and Eötvös was able to conclude that inertial and gravitational mass was equal, to approximately one part in 10^9. In the 20th century, Robert Dicke and others pushed the limit of such an experiment to 10^11, but the Baron's results were sufficient to convince many, including Einstein, that inertial mass and gravitational mass are equivalent. ”

Official Explanation: Selective Gravity

The paradox that external celestial gravity from the Sun and other effects cannot be felt by the test bodies in the torsion balance experiments of Dicke, Eötvös, and others, is acknowledged and addressed by mainstream science with the concept of selective gravity. In the book Gravitation by physicists Charles W. Misner, Kip S. Thorne, and John Archibald Wheeler, on the topic of the Dicke-Eötvös experiments, we read the following at the bottom of p.1055 (Archive):

“ The uniqueness of free fall, as tested by the Dicke-Eötvös experiments, implies that spacetime is filled with a family of preferred curves, the test-body trajectories. ”

The reader is left to decide whether this answer, which was invented for the purpose, is sufficient or valid.