Gravimetry
Gravimetry and Gravity gradiometry is a field of science which supposedly measures the strength of the earth's gravitational field. In these discussions Gravimetry is often used as evidence that the gravitational field of the earth varies with latitude and by location.
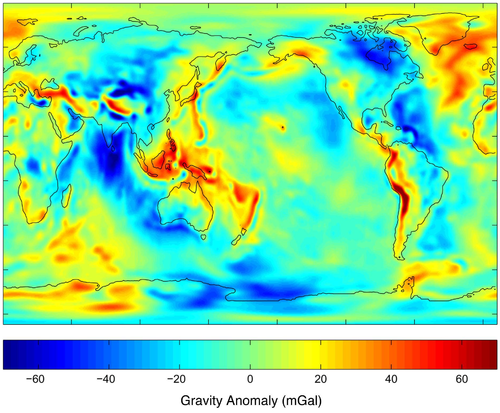
It has been found that Gravimetry is not directly measuring gravity at all. The Gravimeter devices have been described by professionals in that field as long-period seismometers that are measuring small "jerks" in the background seismic noise and interpreting it as variations in gravity.[1] Gravimeters are, in truth, seismometers. Seismometer devices have been described as having a "gravimeter mode."[2] Seismometers can double-purpose as gravimeters, and can detect the "gravity tides". Gravimeters are often similarly double-purposed as seismometers to detect earthquakes thousands of miles away.[3] Perhaps most illustrative, gravitational anomalies on gravity maps are indistinguishable from the seismic zones.[4] Finally, there are several items which do not make sense with the gravity anomalies, if they were actually a measurement of mass.[5]
The differences seen by latitude in the gravimeter are seen to be artificial corrections that are added or subtracted to the data and reference model.[6]
The theory behind the field of Gravimetry is that the masses in the subsurface are creating tiny variations or jerks, presumed to be due to "gravity", that are measured by the devices in a unit of measurement called uGal or mGal. We read a description of Gravity Gradiometry on Wikipedia:
https://en.wikipedia.org/wiki/Gravity_gradiometry (Archive)
“ Gravity gradiometry is the study and measurement of variations in the acceleration due to gravity. The gravity gradient is the spatial rate of change of gravitational acceleration.
Gravity gradiometry is used by oil and mineral prospectors to measure the density of the subsurface, effectively by measuring the rate of change of gravitational acceleration (or jerk) due to underlying rock properties. From this information it is possible to build a picture of subsurface anomalies which can then be used to more accurately target oil, gas and mineral deposits. It is also used to image water column density, when locating submerged objects, or determining water depth (bathymetry). Physical scientists use gravimeters to determine the exact size and shape of the earth and they contribute to the gravity compensations applied to inertial navigation systems. ”
What is Gravimetry?
A quote from the Enhanced Geothermal Innovative Network for Europe (Archive) explains:
“ Gravimetry
As the gravitational field of the earth depends on the density of the rocks, variations of the gravitational field (Bouguer anomalies) observed at the surface or in a borehole are due to density changes in the subsurface, which can be interpreted in terms of changes in the composition and/or geometry of the geological layers. ”
From Gravity surveying: a brief introduction (Archive) we read:
“ Everything is gravitationally attracted to everything else. And the gravitational attraction of an object is proportional to its mass. So if the rocks below you at a given place are denser, then the gravity there will be slightly larger. The changes in gravity from place to place are small: gravity, g, at the Earth’s surface is about 9.81ms−2, but the local variations are a tiny fraction of this; often we are measuring differences of 10−6 ms−2. ”
In The Gravity Method (Archive), its author Dr. Nicolas O. Mariita tells us:
“ The success of the gravity method depends on the different earth materials having different bulk densities (mass) that produce variations in the measured gravitational field. These variations can then be interpreted by a variety of analytical and computers methods to determine the depth, geometry and density that causes the gravity field variations. ”
The Global CCS Institute (Archive) says:
“ Gravimetry consists of studying the anomalies of the gravity field due to density variations underground. ”
Seismometers are Gravimeters
Comparitive Study
Comparative study of superconducting gravimeters and broadband seismometers STS-1/Z in seismic and subseismic frequency bands (Archive)
“ Superconducting gravimeters and broadband seismometers (vertial component) both measure gravity, but whereas the former are most sensitive to very long period signals (gravity tides with periods longer than 6h), the latter are designed for recording the seismic band (elastic normal modes with periods shorter than 1h) ”
Diagram from p. 212:
The paper says that when comparing with Gravimeters to the Seismometers, the gravity spectra is nearly identical:
“ The gravity spectra of the BFO station show that the seismometer STS-1/Z and the superconducting gravimeter are almost equivalent (see also Ritcher et al. (1995)). Therefore we believe that the high noise level shown by the superconducting gravimeter in Strasbourg is probably due to site effects rather than to the instrument itself: a possible reason is that Station J9 is located on a thick layer of sediments (about 3000m) in the Rhine Graben which amplifies noise at long periods. ”
Tidal Detection
Further, the above paper states that seismometers are also able to detect the tides -- p.204, second paragraph:
“ A first attempt to use broadband seismometers outside their traditional spectral range was made by Pillet et al. (1994), and they showed that the STS-1 is able to receive strong tidal signals around diurnal frequencies. ”
It is mentioned that the "gravity tides" are found in the subseismic band:
“ Two different frequency bands are considered: the seismic band (frequencies between 0.2. and 1.667 mHz), for the study of normal modes after the Bolivian earthquake of 9 June 1994, and the subseismic band (frequencies lower than 0.2 mHz), including the study of gravity tides. ”
A definition of "subseismic band" (Archive):
“ "subseismic band" (i.e. frequency lower than 0.03mHz) that has very strong background noise; ”
Is a study of subseismic activity a study of gravity?
Gravimeter Mode
From https://en.wikipedia.org/wiki/Gravimeter (Archive) we read:
“ Many broadband, three axis, seismometers in common use are sensitive enough to track the sun and moon. When operated to report acceleration, they are useful gravimeters. Because they have three axes, it is possible to solve for their position and orientation, by either tracking the arrival time and pattern of seismic waves from earthquakes, or by referencing them to the sun and moon tidal gravity.
Recently, the SGs, and broadband three axis seismometers operated in gravimeter mode, have begun to detect and characterize the small gravity signals from earthquakes. ”
The reader might ask, if gravimeters are entirely different devices than seismometers, how could seismometers have a "gravimeter mode"?
Gravimeters are Seismometers
This inventor describes gravimeters as follows:
http://www.njsas.org/projects/tidal_forces/magnetic_gravimeter/baker/ (Archive)
“ A seismometer usually looks for the smallest possible acceleration changes. Since gravity is physically the same as acceleration, gravimeters are merely versions of seismometers with an infinitely long period response. ”
From p.2 of a paper on seafloor measurements (Archive) from the Journal of Geophysical Research we see:
“ We have collected vertical compliance data using a gravimeter (long- period seismometer) and a differential pressure gauge ”
On p.4 of The Gravity Method (Archive) by Dr. Nicolas O. Mariita we read another reference:
“ An important factor in obtaining useful gravity values in detailed surveys is determining the earth tide effect as their gravitational effects may be greater than the gravity field variations due to the anomalous features being sought. The final aspect of reading a gravity meter concerns seismic activity or cultural movement such as those of vehicles or people. These will disrupt the readings (the meter is actually a low-frequency seismometer) and even though the Scintrex meter has an anti-seismic filter (the La Coste-Romberg meters are also mechanically damped to lessen the effects of earthquakes), readings will still be disrupted. ”
Again, we see that the gravimeter is actually a seismometer, and will be easily disrupted by seismic activity and other noise.
Recall from the above seismometer section that the seismometer was detecting gravity tides on subseismic bands, which was described as:
“ 'subseismic band' (i.e. frequency lower than 0.03mHz) that has very strong background noise ”
Hence, the gravimeter is a low-frequency seismometer, like the seismometer above, taking data out of those low-frequency bands.
On p.14 from a University of Hawaii lecture (Archive) we read:
“ GRAVITY METERS (GRAVIMETERS).
Nearly all gravity surveys use gravimeters to take their data. A gravimeter is identical to a long-period seismometer in most respects, the only difference being that the goal is to measure the force needed to center the mass, which is proportional to g.
This is called a Lacoste suspension. The mass deflects downwards when gravity increases. The adjusting screw changes the length of the spring until the mass is in its centered position. Such instruments are very portable but only measure gravity RELATIVE to some known value. ”
Function of a Gravimeter
It is often argued that a gravimeter works by dropping a body and measuring the full acceleration. While some types of gravimeters drop bodies, others do not. Consider how the following gravimeter works:
https://schmidtocean.org/rv-falkor/operations-and-science-systems/gravimeter/ (Archive)
“ The gravimeter, about the size of a steamer trunk, uses magnetism to suspend an internal metal cylinder, and measures changes in the way gravity pulls on that cylinder. Many people are familiar with the fact that acceleration from gravity—for instance if you jump out of a plane—is 9.8 meters per second squared. Measured in milligals (mGals)—a common research unit for gravity—that’s 980,000. Remarkably, the gravimeter can detect changes as small as 1 mGal—or roughly one millionth of gravity’s total pull. ”
The above device does not contain a falling object. The magnetism suspends the cylinder. The system then measures changes to that cylinder. The article continues:
“ The researchers aren’t interested in that total pull, though; they’re interested in learning about the seafloor. So they process the data coming in to subtract out all the normal weight of Earth below them, which is relatively constant, as well as the weight due to topography, which they get from the sonar mapping. ”
As directly stated, the interest isn't in the total pull. The designers mainly care about using the device as a seismometer.
Absolute Gravimeter Description
From Geophysics From Terrestrial Time‐Variable Gravity Measurements we read about a device that does involve a falling object. The interest is in the tiny noises that affect the mirror in the device:
“ In an absolute gravimeter, a test laser beam bounces off the free‐falling body before being reflected back to the interferometer, where the test beam interferes with a reference one. While the dropped mass is completely isolated from the Earth's vibrations during its fall, anthropogenic and natural microseismic noises continuously modify the position of the reference mirror of the interferometer. Even in the absence of an earthquake, the displacements of the Earth's surface are persistent and location and season dependent, reaching up to a few micrometers close to the coast (Kedar et al., 2008), while one should measure the free‐fall distance at the 1 nm precision level in order to achieve a precision on gravity of 10 nm/s^2. In the first white‐light gravimeter, the measurements of gravity were corrected by using the records from a 1 s period seismometer. Early in the 1980s, Rinker (1983) developed the so‐called Super Spring, that is, a modified seismometer providing an inertial reference system at periods shorter than about 1 min—the suspended mass of a seismometer provides an inertial reference frame, independent from the motions of the Earth, at periods shorter than the resonance frequency (Aki & Richards, 2002). The challenge consisted in producing a suspension device of which the free period is about 1 min, that is, longer than the periods ranging 5–20 s, where microseism is the strongest. ”
Monitoring earthquakes with gravity meters
From the abstract of a paper titled Monitoring earthquakes with gravity meters (Archive) we read:
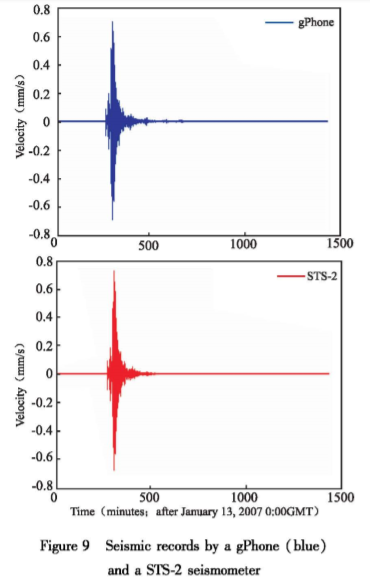
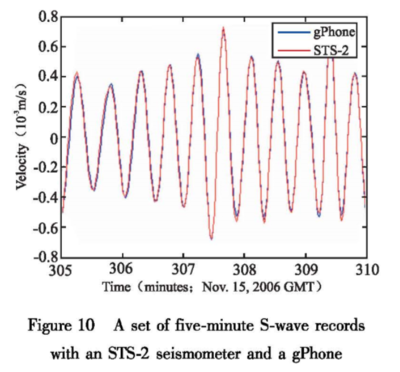
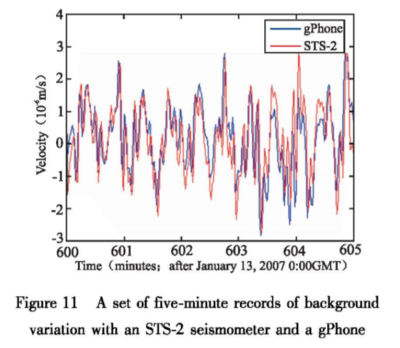
“ Seismic waves from a magnitude 8.3 earthquake in Japan were consistently recorded by five nearly identical gPhone gravity meters in Colorado. Good correlation was also found in the response of two different types of gravity meters and a standard seismometer in Walferdange, Luxembourg to an earthquake of magnitude 8.2 in Japan, indicating that all of them were capable of measuring the surface waves reliably. The gravity meters, however, recorded 11 separate arrivals of Raleigh waves, while the seismometer only one. Thus the gravity meters may be useful for obtaining new information in the study of seismic velocities, attenuation and dispersion. ”
The ending two sentences of that abstract even imply that gravity meters may be superior for measuring seismic elements.
Earthquake Comparison Readings
From the study we see several seismic reading comparisons between gravimeters and seismometers:
Gravity anomalies observed before earthquakes
Pre-seismic gravity anomalies before Linkou Ms 6.4 earthquake by continuous gravity observation of Crustal Movement Observation Network of China (Archive)
The reader may ponder why the gravity of the earth would change before an earthquake.
Corrections for Latitude
It is asserted that gravimetry has shown trends at different latitudes, and so this is validation of the idea that it is really measuring "gravity". We find that this assertion is unfounded.
From a university course on gravity surveying we read:
http://www.geol-amu.org/notes/m10-1-4.htm (Archive)
“ Recall that, if the Earth were an homogeneous ellipsoid, the value of gravity at the surface would be given by:
g = g0 (1 + k1 sin2 ϕ – k2 sin2 2ϕ)
The objective of gravity surveys is to look for deviations from this reference value. ”
If the objective of gravity surveys is merely to look for deviations from a round earth reference model with the vibrating gravity theory, then the final computed number in meters per second squared would becomes meaningless for the purpose of discussion. Any modifications to the reference values are constructed on an entirely theoretical basis.
The above page tells us that there is a theoretical model and that the goal of gravity surveys is to modify that model. Further down we see, among the list of corrections to be made, the latitude correction:
“ Latitude correction: The earth's poles are closer to the centre of the equator than is the equator. However, there is more mass under the equator and there is an opposing centrifugal acceleration at the equator. The net effect is that gravity is greater at the poles than the equator.
For values relative to a base station, gravity increases as you move north, so subtract 0.811 sin(2a) mGal/km as you move north from the base station. (where a is latitude). ”
We read that we are subtracting or adding values to the reference model and the data to make the corrections for latitude, which is very different than using the data to determine the latitude. The claim that the final number is meaningful as evidence to showcase any particular point is shown fallacious.
United Nations University
On p.9 of Seismic Activity, Gravity, and Magnetic Measurements (Archive) by LaGeo as part of the United Nations University Geothermal Training Program we read:
“ 3.6 Reduction of data
Gravimeters do not give direct measurements of gravity; rather, a meter reading is taken which is then multiplied by an instrumental calibration factor to produce a value of observed gravity (known as gobs). The correction process is known as gravity data reduction or reduction to the geoid. The various corrections that can be applied are the following. ”
The section goes on to list a number of corrections, including corrections for latitude and elevation, which is not data contained in the measurement readings:
“ Latitude correction (gn) - Correction subtracted from gobs that accounts for earth's elliptical shape and rotation. The gravity value that would be observed if the earth were a perfect (no geologic or topographic complexities) rotating ellipsoid is referred to as the normal gravity. ”
“ Free-air corrected gravity (gfa) - The free-air correction accounts for gravity variations caused by elevation differences in the observation locations ”
These are artificial corrections which are added or subtracted to the data and reference model. If the earth were really elliptical or rotating, then these artificial corrections would not be necessary.
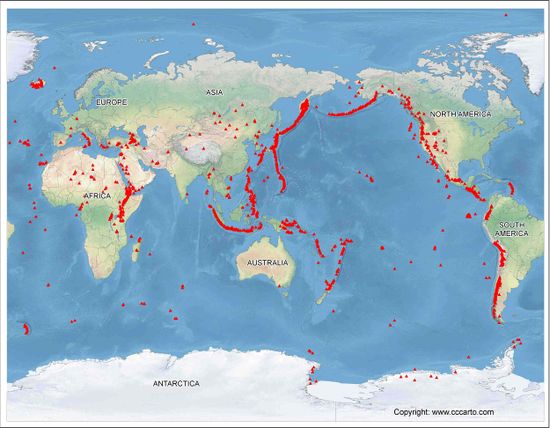
Seismic Map Similarities
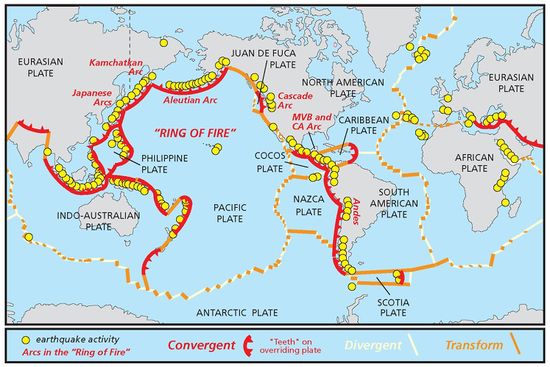
Convergent Plate and Earthquake Map
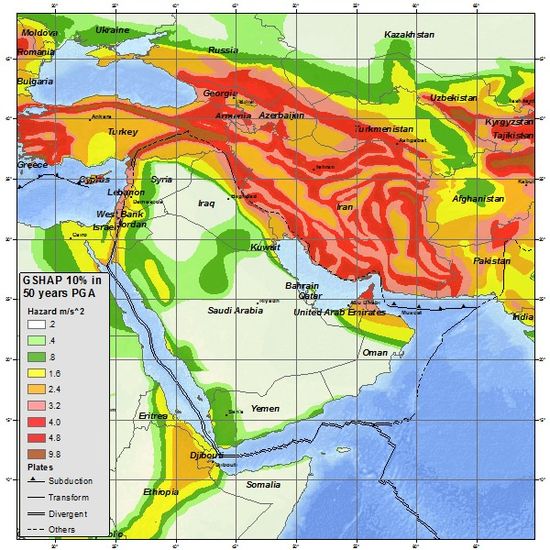
Compare the gravity anomalies to a map of the plate boundaries and the earthquake zones:
Convergent Plates Map Source (Archive)
World Volcano Map
World Volcano Map Source p.10 (Archive)
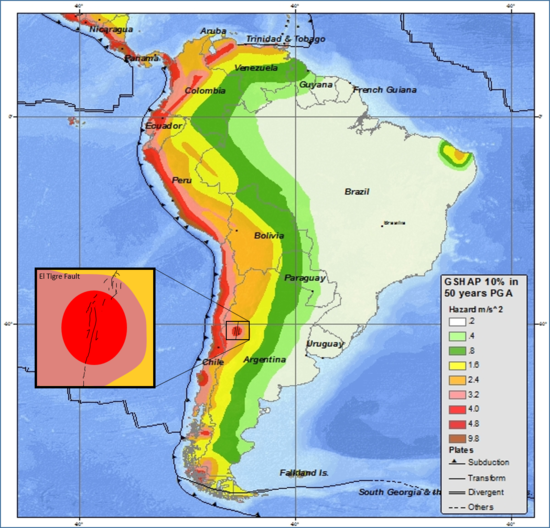
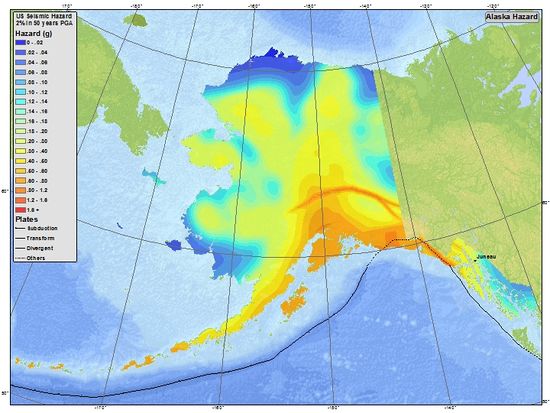
Seismic Hazard Maps
South America Seismic Hazard Map Source (Archive)
Alaska Seismic Hazard Map Source (Archive)
Perplexing Anomalies
The anomalous deviations of gravity, as detected by the gravmieter, are called Bouguer Anomalies.
https://en.wikipedia.org/wiki/Bouguer_anomaly (Archive) explains:
“ In geodesy and geophysics, the Bouguer anomaly (named after Pierre Bouguer) is a gravity anomaly, corrected for the height at which it is measured and the attraction of terrain. The height correction alone gives a free-air gravity anomaly.
Anomaly
The Bouguer anomaly is related to the observed gravity gobs as follows:
gB = gobs - gλ + δgF + δgB + δgT
gB = gF - δgB
gB is the Bouguer anomaly;
gobs is the observed gravity;
gλ is the correction for latitude (because the Earth is not a perfect sphere);
δgF is the free-air correction;
δgB is the Bouguer correction which allows for the gravitational attraction of rocks between the measurement point and sea level;
gF is the free-air gravity anomaly.
δgT is a terrain correction which allows for deviations of the surface from an infinite horizontal plane ”
Note that a correction for latitude needs to be made, and that the data is not in the gravimeter readings itself.
Gravity Anomalies Contrary To Theory
"Bouguer Anomalies Over The Continents and Oceans" in the Journal of the Geological Society of India tells us that the anomalies are often greater over the ocean than over the land, which is contrary to gravity theory:
“ Why, in general, the Bouguer gravity anomalies are negative in continental areas and positive in oceanic areas? Extending the question further, why do the predominant negative and positive anomalies respectively correspond to the mountain peaks and ocean depths? Although the Bouguer gravity data are not brought on to an even datum, there is fairly a good inverse correlation of Bouguer anomalies with height/depth as well as seismic data. This obviously indicates the excess mass reflected as gravity lows and the deficit mass as gravity highs with respect to the geoid/ellipsoid surface. This is in contrast to the theory of the gravity field which is proportional to the excess or deficit mass. Mathematically speaking, the observed anomalies are proportional to the vertical gradient of gravity, indicating excess mass above the geoid as gravity lows and deficit mass below the geoid as gravity highs. If this were true, far reaching implications arise in the understanding of the theory and interpretation of Bouguer anomalies. ”
The anomalies are negative in continental areas and positive in oceanic areas. The anomalies are also negative in the mountains. These anomalies appear to go against the theory that the anomalies are due to the attraction of mass.
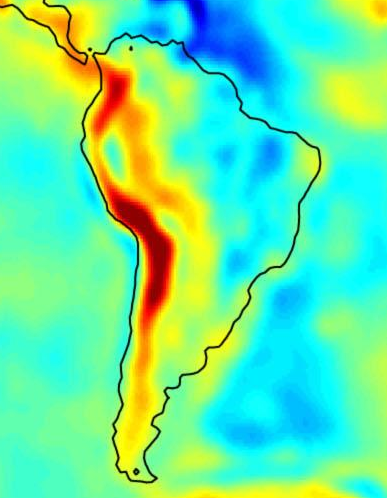
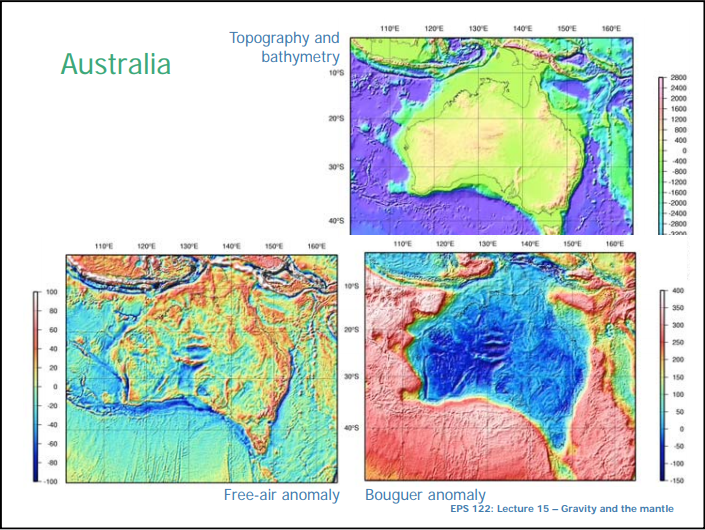
Bouguer Anomalies - Australia
We find the following depiction of Australia's Complete Bouguer Anomalies and Free Air Anomalies on a University of California Berkeley lecture on gravimetry (Archive) p.3, showing that the anomalies are negative over continental areas and positive over oceanic areas:
Bouguer Anomalies - Alps of Germany
https://www.leibniz-liag.de/en/research/methods/gravimetry-magnetics/bouguer-anomalies.html (Archive)
“ This map shows the Bouguer anomalies over the whole of Germany and surrounding areas, in a detailed but still clear way.
...The resulting gravity anomalies vary across the mapped area from -170 mGal in the Alps to +40 mGal around the gravity low in the Magdeburg area. ”
The above map and description shows that the anomalies are negative in the Alps of Germany.
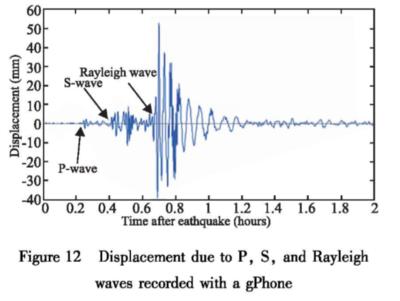
Seismic Wave Propagation
Background Seismic Noise
It should be noted that there is constant background seismic noise, which emanate from the earth. From http://microglacoste.com/gPhoneNoise/gPhoneSeismicNoise.pdf (Archive) we read:
“ It is interesting to speculate on the precise origin of the background seismic noise. Haubrich et al ii for example, open their article with the following description of the seismic noise background and the large interest it has generated over the years as well as the intractability of its investigation:
The low‐level background unrest of the earth, called microseisms or earth noise, has puzzled seismologists and other scientists for nearly a century. The problem of its nature and causes has proved particularly unyielding, not, however, for lack of investigation. A bibliography covering work up to 1955 [Gutenberg and Andrews, 1956] iii lists over 600 articles on the subject; one covering the years from 1955 to 1964 [Hjortenberg, 1967] iv lists 566. Unfortunately, much of this work has advanced the subject but slightly. ”
Airborne Seismic Waves
It should also be noted that seismic waves can become airborne, which would explain the ability of gravimeter devices on airplanes to register the anomalies.
https://en.wikipedia.org/wiki/Seismic_wave (Archive)
“ Primary waves (P-waves) are compressional waves that are longitudinal in nature. P waves are pressure waves that travel faster than other waves through the earth to arrive at seismograph stations first, hence the name "Primary". These waves can travel through any type of material, including fluids, and can travel nearly 1.7 times faster than the S waves. In air, they take the form of sound waves, hence they travel at the speed of sound. Typical speeds are 330 m/s in air, 1450 m/s in water and about 5000 m/s in granite. ”
Noise Analysis
On analysis of the gravimeter we find its primary purpose is to measur noise and use many software algorithms to interpret and filter out the noise. Every part of the device's components—the lasers which measure the motion, the mirrors, the springs which launch the mass up and down the small tube, and all component parts—are all connected in some manner to the earth, and are subject to noise and vibrations.
https://link.springer.com/chapter/10.1007/978-3-662-03482-8_9 (Archive p.1 p.2)
“ One of the most serious problems for absolute gravimeters is the vibration disturbances. ”
Marine Gravimeters
Below we see an example of gravimetry devices and methods for marine gravimetric surveying:
http://www.iitk.ac.in/nicee/wcee/article/WCEE2012_1237.pdf (Archive)
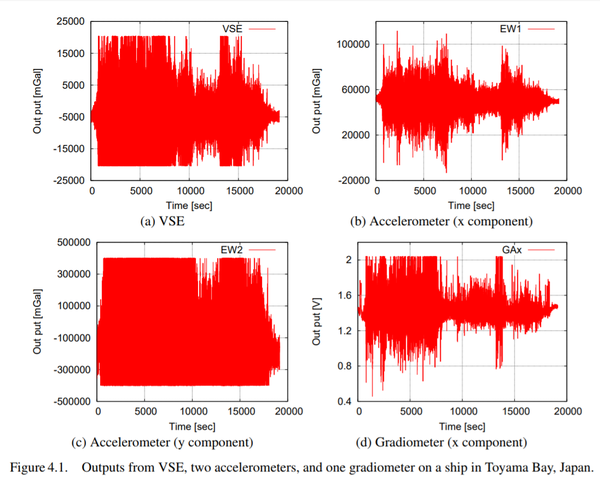
An example is given of outputs from VSE, Accelerometer, and Gradiometer devices on a mid-size ship navigating Toyama Bay, Japan:
Following the illustration we find the following:
“ FINDING GRAVITY FROM VERY NOISY DATA
In the previous section, the low-pass filter is used to find the gravity from the noisy data. We can expect that the variation of gravity consists of components with long period, however the vibration of carrier with short period. If this expectation is satisfied, the low-pass filter should work well. Actually, analysis for the first observation on an observation wheel works well, though, not for the other two observations. The reason is the difference of the amplitude of the noise: it is very difficult to pick up the gravity data with very small amplitude from very large vibration of the carrier. This must be limitation of simple filtering technique.
To reduce the vibration of the carrier, we can choose two different approaches. ”
From the above we see that a need to use algorithms and filters to 'find gravity' from noise. The levels of g are not readily apparent, and must be constructed by subtracting from the noise to 'find gravity'. The above passage states that "We can expect to find the variations of gravity consists of components with long period, however the vibration of the carrier with short periods."
The reader may decide whether the process of subtracting vibrations with one characteristic to reveal other vibrations is truly measuring gravity. Why does "gravity" need to be found?
Galathea-3: A global marine gravity profile
The Danish vessel Galathea-3 describes its methods for gravimetric surveying:
Galathea-3: A Global Marine Gravity Profile (Archive)
“ The Galathea-3 navigation data included raw depth records provided by The Danish Hydrological Office. The data transfer was sometimes unstable and the data themselves were often very noisy. A preparation of such data for the Bouguer gravity processing requires a cumbersome data cleaning the removal of the spikes, the smoothing, and often the interpolation ”
We see that the process involves extensive data analysis, filtering, and cleanup from noise — to 'find gravity'.
Airborne Gravimetry
Airborne gravimetery methods reviel the same:
Improving the Accuracy and Resolution of SINS/DGPS Airborne Gravimetry (Archive)
“ Because the resulting signal is very noisy (see Sections 2.3.2 to 2.3.4 for details), its derivation is followed by a filtering step that removes most of the noise by low-pass filtering the data. ”
Again, we see that filtering is necessary to clean up the noise.
General/Land Based Gravimetry
The following paper describes the process of turning a laser signal into a "variation of gravity":
Ultra-high Precision, Absolute, Earth Gravity Measurements (Archive)
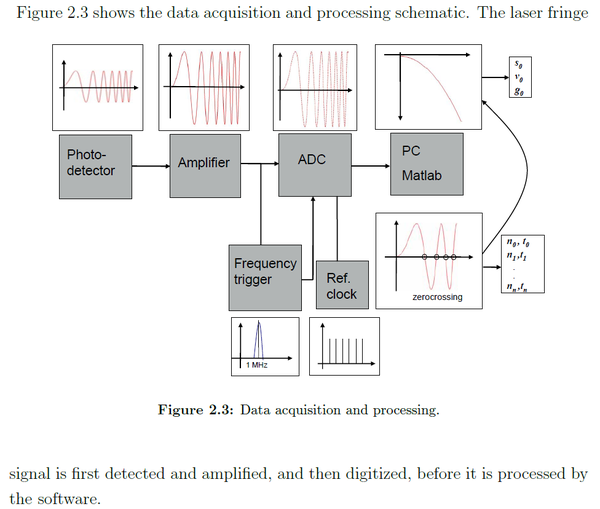
The paper describes that the fringe signal from the laser beam is digitized and processed:
“ One of the new features of our setup is that the whole fringe signal (with up to 1.6 million data points) is digitized and processed. In other gravimeters usually just parts of the fringe signal are used for data processing. Since the duration of our FB’s fall in the MPG-1 is about 200 ms, the resultant signal reaches a frequency of up to 6.2 MHz. As an industry standard, a sampling rate of at least 7 times the measured frequency is suggested. ”
Processing Steps
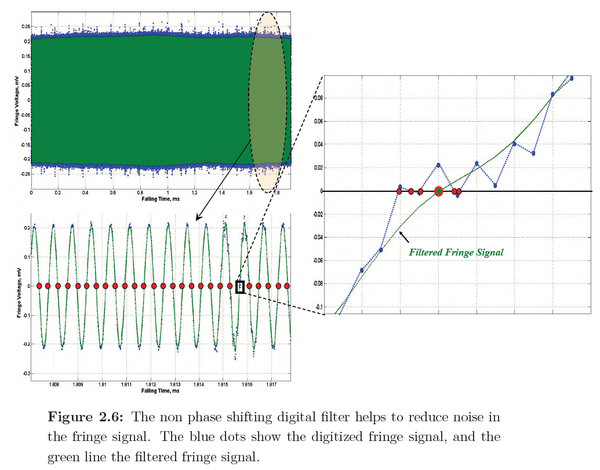
The fringe signal from the laser must be filtered with software:
The remainder of the document describes how the filtering occurs. All sources, to the best of the author's ability, are given an "uncertainty budget," to which is subtracted from the noise. The uncertainty budgets are estimated ranges to which a phenomenon may be contributing to the noise. All possible phenomena in nature must be considered and precisely defined. Everything from air drag, electrostatic fields, pressure, seismic vibrations, &c.
In the Table of Contents we find a list of tables, showing the various elements which are subtracted:
4.6 Uncertainty budget of the measured imbalance – Method II. . . . 84
4.7 Uncertainty budget: COM and OC adjusted – Method II. . . . . . 84
5.1 Uncertainty budget for air drag . . . . . . . . . . . . . . . . . . . 89
5.2 Uncertainty budget for outgassing . . . . . . . . . . . . . . . . . . 90
5.3 Uncertainty budget for eddy currents . . . . . . . . . . . . . . . . 91
5.4 Uncertainty budget for electrostatic field . . . . . . . . . . . . . . 91
5.5 Uncertainty budget for instrumental masses . . . . . . . . . . . . 94
5.6 Uncertainty budget for laser verticality . . . . . . . . . . . . . . . 96
5.7 Length standard specifications. . . . . . . . . . . . . . . . . . . . 96
5.8 Uncertainty budget for laser stability . . . . . . . . . . . . . . . . 97
5.9 Frequency standard specifications. . . . . . . . . . . . . . . . . . . 98
5.10 Uncertainty budget for clock stability . . . . . . . . . . . . . . . . 98
5.11 Uncertainty budget for corner cube rotation . . . . . . . . . . . . 98
5.12 Uncertainty budget for radiation pressure . . . . . . . . . . . . . . 99
5.13 Uncertainty budget for beam divergence . . . . . . . . . . . . . . 100
5.14 Uncertainty budget for temperature gradient . . . . . . . . . . . . 101
5.15 Uncertainty budget for seismic noise . . . . . . . . . . . . . . . . 107
5.16 Uncertainty budget for speed of light . . . . . . . . . . . . . . . . 108
5.17 Uncertainty budget for effective height . . . . . . . . . . . . . . . 109
5.18 Specifications of Photoreceiver. . . . . . . . . . . . . . . . . . . . 110
5.19 Uncertainty budget for amplifier . . . . . . . . . . . . . . . . . . . 111
5.20 Uncertainty budget for solid Earth tides . . . . . . . . . . . . . . 113
5.21 Uncertainty budget for ocean loading . . . . . . . . . . . . . . . . 113
5.22 Uncertainty budget for polar motion . . . . . . . . . . . . . . . . 114
5.23 Uncertainty budget for environmental pressure . . . . . . . . . . . 115
5.24 Uncertainty budget for Coriolis force . . . . . . . . . . . . . . . . 116
5.25 Uncertainty budget for MPG-1. . . . . . . . . . . . . . . . . . . . 117
5.26 Uncertainty budget for MPG-2. . . . . . . . . . . . . . . . . . . . 118
Once all of these items and their theoretical uncertainties are subtracted, we are left with "gravity".
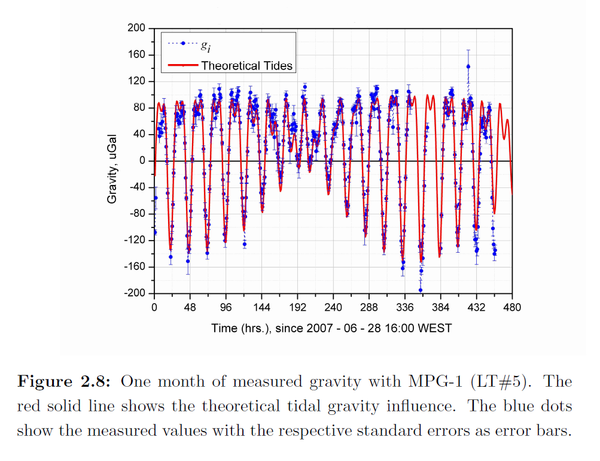
Gravimeter Tides
The above pdf mentions that long-term analysis of the gravimeter noise can detect the tides:
The main conclusion from this is that the tides may be related in some manner to vibration or noise that is being processed. No mechanism is presented, or is identifiable, from a long term analysis of noise trends.
Fringe Noise
We look at the following paper:
From the introduction the author states that the input is a noisy fringe signal.
“ The advantages of digitizing the entire fringe signal are as follows: the imperfect electronic components are eliminated; the full information on the quality of the fringe signal is available; a noisy fringe signal is digitally filtered at the pre-processing steps; different numerical algorithms to calculate a g value can be interchangeably applied. ”
The g value must be extracted with various methods. It is not direct and apparent:
“ Usually, the fringe signal is digitized at a sampling rate exceeding its maximum frequency. However, a few methods have demonstrated the possibility to extract a g value from the fringe signal sampled far below the Nyquist criterion (table 1). ”
Multiple methods, functions, to "extract" the gravity value from the "noisy fringe signal."
Not an obvious and apparent method; multiple models are involved:
“ This method has been developed by Niebauer et al [18]. The basic idea is to extract the gravity value directly from the undersampled waveform of the fringe signal given by the non-linear model (1). To find the initial estimates of the model parameters, required in the non-linear leastsquares adjustment, it was proposed to iteratively demodulate the digitized waveform. For this the acquired fringe signal is multiplied by a swept sinusoid, denoted as a complex heterodyne function. This method requires prior knowledge of the sweep parameters. A complex heterodyning is used to reduce the bandwidth of the demodulated signal in order to double the signal-to-noise ratio, compared with a singlesideband demodulation [18]. ”
Filtering agreement can be made with other fringe signal processing methods:
“ Up to now, a few comparisons of different fringe signal processing methods have reported an agreement within several parts in 10^9 of g [10, 18] or even larger [12, 16]. ”
These processes are filtering out the noise to find trends. From the conclusion we read:
“ 5. Conclusions
For the first time, a comparison of the three different digital fringe signal processing methods, realized in the same absolute gravimeter, has been completed. The two-sample zerocrossing method, the windowed second-difference method and the method of non-linear least-squares adjustment using the initial parameter estimates, found by the demodulation of the undersampled fringe signal, have been compared in numerical simulations, hardware tests and actual measurements with the MPG-2 absolute gravimeter. Up to now, diversity of the digital fringe signal processing methods in absolute gravimetry was mainly caused by a certain technical restriction: processing of the huge amount of digitized fringe data was limited by the available computing capabilities. Owing to this, several original, though complicated, algorithms have been developed. In contrast, the reported comparison involves the simple and straightforward method to detect all the zero-crossings in a digitized fringe signal. ”
This document was written in 2010. If Gravimetry were really 'direct measurement of the acceleration,' as some have claimed, then the reader might ask, why was it limited by pre-2010 computing capabilities? The answer is that it is not direct at all. It is the many algorithms necessary to interpret the "noisy" fringe signal that need large amounts of computing power. The process is interpretation of a noisy fringe signal.
From the paper:
“ Therefore, a combination of the different methods of fringe signal processing in the same instrument is a useful tool to compose a more complete uncertainty budget. ”
Uncertainty budgets, just as we saw in the earlier paper, are subtracted from the noise in the effort to find gravity.