Difference between revisions of "Planets"
Tom Bishop (talk | contribs) (→Topics) |
Tom Bishop (talk | contribs) |
||
| Line 185: | Line 185: | ||
{{cite2|People need to be aware that there is a range of models that could explain the observations. For instance, I can construct you a spherically symmetrical universe with Earth at its center, and you cannot disprove it based on observations. You can only exclude it on philosophical grounds. In my view there is absolutely nothing wrong in that. What I want to bring into the open is the fact that we are using philosophical criteria in choosing our models. A lot of cosmology tries to hide that.|Cosmologist George Ellis in Scientific American, "Thinking Globally, Acting Universally", October 1995}} | {{cite2|People need to be aware that there is a range of models that could explain the observations. For instance, I can construct you a spherically symmetrical universe with Earth at its center, and you cannot disprove it based on observations. You can only exclude it on philosophical grounds. In my view there is absolutely nothing wrong in that. What I want to bring into the open is the fact that we are using philosophical criteria in choosing our models. A lot of cosmology tries to hide that.|Cosmologist George Ellis in Scientific American, "Thinking Globally, Acting Universally", October 1995}} | ||
| + | ==Topics== | ||
| + | ''Round Earth Topics'' | ||
| + | |||
| + | :*[[Discovery of Neptune]] - A claim that Neptune was discovered through mathematics alone | ||
| + | :*[[Precession of Mercury's Orbit]] - Einstein's use of Mercury as evidence of Relativity | ||
| + | |||
| + | ''Flat Earth Topics'' | ||
| + | |||
| + | :*[[Kings Dethroned]] - A text questioning astronomical triangulation methods | ||
| + | :*[[Astronomical Prediction Based on Patterns]] - Epicycles are still used for astronomical prediction | ||
| + | :*[[Three Body Problem]] - The heliocentric Sun-Earth-Moon system cannot be simulated | ||
[[Category:Planets]] | [[Category:Planets]] | ||
Revision as of 03:43, 31 January 2021
The planets are spherical bodies which revolve above the Earth. The planets follow a similar daily route across the sky as the Sun. Five planets — Mercury, Venus, Mars, Jupiter, and Saturn are visible to the naked eye and were known to the ancients as "wandering stars;" entities which appear to move differently from the fixed path of the stars. The word "planet" comes from the Greek word planetes, meaning "wanderer."
On the topic of the history of the planets and the invention and acceptance of the heliocentric system, by the time of Copernicus and Galileo it was already widely believed that the Earth was a globe, largely based on Ancient Greek knowledge. The debate was whether the Sun was a central point of rotation for the Solar System, and if so, whether the Earth was in motion and moving in it. There is some agreement in the Flat Earth movement that they had gotten some things right, such as the Sun being a central body for the planets, since that is the most natural inclination when one sees Mercury and Venus following the Sun in the sky and moving to either side of it. In this sense, it may be accepted that the Solar System is Heliocentric or semi-Heliocentric under the Flat Earth model. However, from viewing the motions of the planets above us, it does not necessarily follow that the Earth is a planet in the Solar System. The Earth is a fundamentally different kind of body; a plane rather than a planet, much like how a basketball court is a fundamentally different kind of body to the basketballs which bounce on top of it. The Solar System sits in a layer above the plane of the Earth.
Dance of the Planets
The Sun moves in Northward and Southwards paths across the sky over the course of the year when changing seasons and the planets follow along that path, with an apparent relationship to the Sun. Mercury and Venus appear to be rotating around the Sun, while the other planets have a less direct effect. The below animation shows the Sun's progress across the sky over the course of a year as a panorama, its Northward and Southward motions, and the 'dance of the planets' as they follow the sun. The daily paths across the sky are subtracted, showing yearly movement.
(Source)
The Copernican Revolution of the 16th century held that this relationship with the Sun was evidence that all of the planets of the Solar System moved around the Sun. At the time the idea of a Round Earth was already widely prevalent, based on the teachings of the Ancient Greeks. It was deduced that since the Earth is a round body in a Sun-centered celestial system, that the earth must also be a body in motion similar to the planets seen in the sky.
Flat Earth System
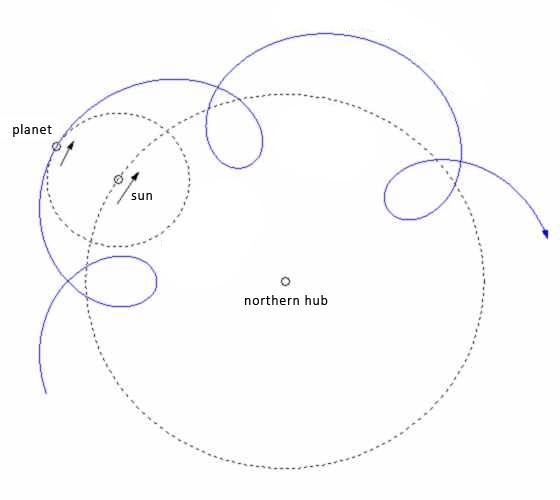
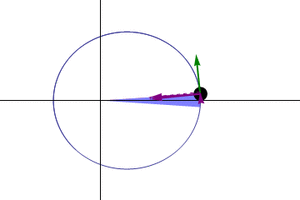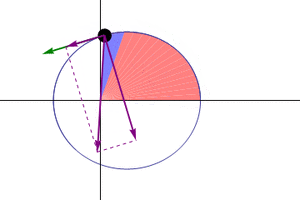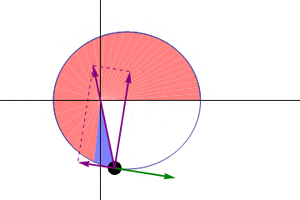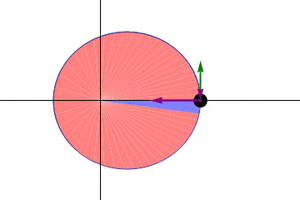
Under a Flat Earth model with a mobile Sun, the retrograde loops may be explained by the planets revolving around the Sun, while the Sun and planets simultaneously move around the hub of the earth. The planets are moving very slowly around the Sun and the hub, in circles or ellipses of various sizes in particular to the planet, as the Sun moves around the center. Over time this disagreement in movement can create retrograde loops seen in the sky.
The speed of the planet around the circle and its size may define the rate of retrograde. Some advocate for a "neo-tychonian" system similar in concept to Tycho Brahe's[1] semi-heliocentric planet model which featured a mobile sun which rotates around the earth once a day while the planets revolve around the Sun with various orbital circumferences. With a Flat Earth interpretation Mercury and Venus would rotate around the Sun near to it while the superior planets rotate around the Sun on larger circles encompassing the northern pole on paths similar to the Sun's main path, and which sit between the tropics.
Superior Planets
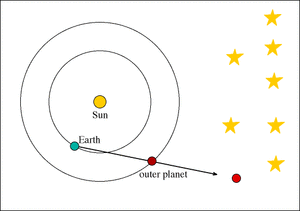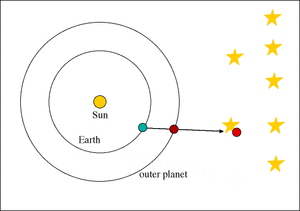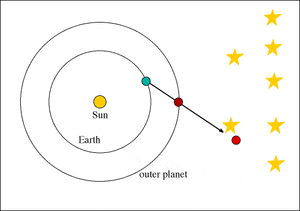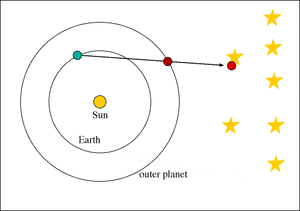
In the Flat Earth model the stars are in motion above the earth, at a rate of one rotation every 23 hours 56 minutes. If a planet is not matching this rate of rotation it may appear to either lag behind or move faster than the stars. One contribution to astronomy was by the German astronomer Johannes Kepler, who found that the rate of a planet's speed changes over the course of its orbit. When a planet is close to the Sun it is moving faster, and when a planet is far from the sun it is moving slower.
Kepler suggested magnetism as a basis for this attraction, while Newton suggested a phenomenon called gravity. Immaterial of mechanism, however, this concept suggests that planets slow down or speed up depending on their proximity the Sun. Notice how in the Dance of the Planets animation above that Saturn and Jupiter progress and move faster than the stars when the Sun is approaching their vicinity, and that they regress and move slower than the stars when the Sun is far away from them. This pattern of movement is similar to Kepler's depiction of elliptical orbits, provides an explanation for the retrograde, and suggests that the planets are connected to the Sun.
Related
- Video: Flat Earth Planets - Mercury Retrograde (Runtime 7m20s) — User 'Alternative Cosmology' makes several observations on the topic of Mercury's Retrograde under the context of a Flat Earth model.
History
“ Accordingly, since nothing prevents the earth from moving, I suggest that we should now consider also whether several motions suit it, so that it can be regarded as one of the planets. For, it is not the center of all the revolutions. ”
—Nicolaus Copernicus
“ I demonstrate by means of philosophy that the earth is round, and is inhabited on all sides; that it is insignificantly small, and is borne through the stars. ”
—Johannes Kepler
“ In the middle of all sits Sun enthroned. In this most beautiful temple could we place this luminary in any better position from which he can illuminate the whole at once? He is rightly called the Lamp, the Mind, the Ruler of the Universe: Hermes Trismegistus names him the Visible God, Sophocles’ Electra calls him the All-seeing. So the Sun sits as upon a royal throne ruling his children the planets which circle round him. The Earth has the Moon at her service. As Aristotle says, in his On Animals, the Moon has the closest relationship with the Earth. Meanwhile the Earth conceives by the Sun, and becomes pregnant with an annual rebirth. ”
—Nicolaus Copernicus , De Revolutionibus, Of the Order of the Heavenly Bodies 10.
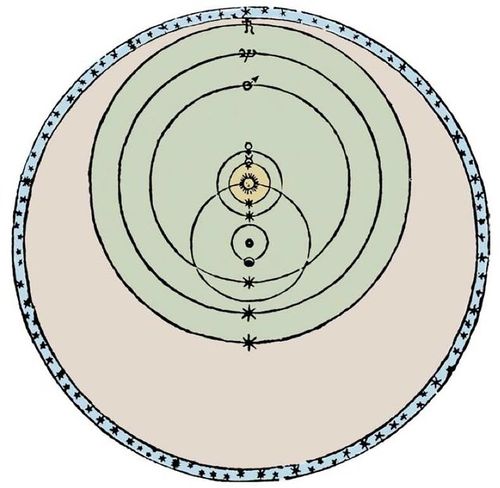
Ptolemaic System
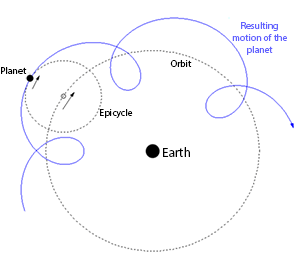
Prior to the heliocentric system of Copernicus the prevailing astronomical model featured an earth-centered system, with main attribution to mathematician and astronomer Claudius Ptolemy. The Earth was round and at the center of this system while the planets moved around it on epicycles - a small circle whose center moves around the circumference of a larger one. However, this was considered to be a mathematical construct rather than a geometric one, the epicycles being a mathematical method to predict patterns of movement. Its authors felt that prediction was more important than a geometric depiction of the system. In Beyond Reason: Essays on the Philosophy of Paul Feyerabend its author, philosopher of science Paul Feyerabend (bio), describes Ptolemy's construct:
“ Ptolemy continually seeks to chart and predict “the appearances” - the points of light on the celestial globe. The Almagest abandons any attempt to explain the machinery behind these appearances. Apollonius, Hipparchus, and Claudius Ptolemy decide in favor of inventing abstract mathematic devices. They view the provision of an explanation of celestial motions as beyond human powers ....49
The great astronomers of the ancient world ... — Eudoxus, Apollonius, Hipparchos, Claudius Ptolemy — could predict where planets and stars would appear at future dates. But each explicitly rules out the possibility of explaining the physics behind the apparent motions of the cosmos Indeed, the history of planetary theory could be viewed as conceptual struggle between two opposed forces, the urge to explain and the urge to predict .... Ptolemy sacrificed a philosophically coherent and unified picture of the heavens in favor of an accurate instrument of forecast ...
Ptolemy stressed that he could never hope to explain the wanderings of the planets. His inspiration was only to find a geometrical calculus through which he might forecast when next a given planet would halt in its eastward motion, “back-up” a few degrees, and then continue forward again. Understanding beyond this exceeded Ptolemy’s objectives. The Almagest was but a computational machine; it had some success in saying when celestial events might occur, but did not even undertake to ask why they occurred.50
~
Ptolemy was content to “save appearances” and did not speculate about the underlying fabric of the heavens. He did not even care whether the mathematical constructions he used for astronomical purposes were consistent with one another .... Whenever two constructions yields equivalent mathematical results, there was, in Ptolemy’s view, no astronomical difference between them. We are at liberty to account for the one anomaly in terms of “eccentrics” and the other in terms of “epicycles” - whichever way round we please. So far as Ptolemy is concerned, the question of the physical reality or unreality of these motions is beside the point ...
From the physicist’s point of view, the equant was a very unsatisfactory device. Mathematically it might do a job, but there was something intrinsically mireasonable about it. Ptolemy thought physics irrelevant to astronomy, and confined himself to mathematics.52
On the one hand was the subject of descriptive and physical cosmology, predominantly Aristotelian .... On the other hand was the highly complex mathematical theory concerned with the phenomenological determination and prediction of the irregularities of planetary motions .... We shall call this mathematical theory “Ptolemaic Theory”, ... There are many widespread misconceptions about this Ptolemaic Theory ... First, there never was such a thing ... as a Ptolemaic System. The complex mathematical theory is arranged so as to deal with each planet separately and individually. There is no single mathematical connection between these several models, only a general similarity in the methods used for each.53 ”
Copernican System
The Copernican System, introduced in 1543, attempted to move the Ptolemaic System forward by proposing a Sun-centered geometric solar system. The main pieces of evidence for this model were the motions of Mercury and Venus being more physically pleasing with a Sun as center point, the retrograde motion of Mars as the result of a Sun-centered system, and the fact that Jupiter had moons (Galileo) -- a piece of evidence that the Earth was not necessarily the center of everything as Ptolmy suggested. However, to explain the retrogrades as a Sun-centered system, this model still introduced complexities elsewhere. The complex and physically unpleasing mathematical constructs of epicycles were still in the Copernican system, rearranged in a way so that the Sun was at the center. Despite the complexity necessary for prediction, it was argued that the concept of a Sun-centered system was more philosophically pleasing.
What Is This Thing Called Science? (Archive)
By Prof. Alan Chalmers (bio)
“ In View of the strength of the case against Copernicus, it might well be asked just what there was to be said in favour of the Copernican theory in 1543. The answer is, ‘not very much’. The main attraction of the Copernican theory lay in the neat way it explained a number of features of planetary motion, which could be explained in the rival Ptolemaic theory only in an unattractive, artificial way. The features are the retrograde motion of the planets and the fact that, unlike the other planets, Mercury and Venus always remain in the proximity of the sun. A planet at regular intervals regresses, that is, stops its westward motion among the stars (as viewed from earth) and for a short time retraces its path eastward before continuing its journey westward once again. In the Ptolemaic system, retrograde motion was explained by the somewhat ad hoc maneuver of adding epicycles especially designed for the purpose. In the Copernican system, no such artificial move is necessary. Retrograde motion is a natural consequence of the fact that the earth and the planets together orbit the sun against the background of the fixed stars. Similar remarks apply to the problem of the constant proximity of the sun, Mercury and Venus. This is a natural consequence of the Copernican system once it is established that the orbits of Mercury and Venus are inside that of the earth. In the Ptolemaic system, the orbits of the sun, Mercury and Venus have to be artificially linked together to achieve the required result.
Thus there were some mathematical features of the Copernican theory that were in its favour. Apart from these, the two rival systems were more or less on a par as far as simplicity and accord with observations of planetary positions are concerned. Circular sun-centred orbits cannot be reconciled with observation, so that Copernicus, like Ptolemy, needed to add epicycles, and the total number of epicycles needed to produce orbits in accord with known observations was about the same for the two systems. In 1543 the arguments from mathematical simplicity that worked in favour of Copernicus could not be regarded as an adequate counter to the mechanical and astronomical arguments that worked against him. Nevertheless, a number of mathematically capable natural philosophers were to be attracted to the Copernican system, and their efforts to defend it became increasingly successful over the next hundred years or so. ”
Comparison
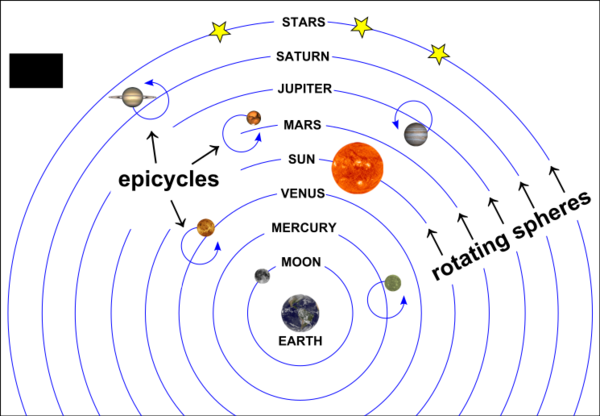
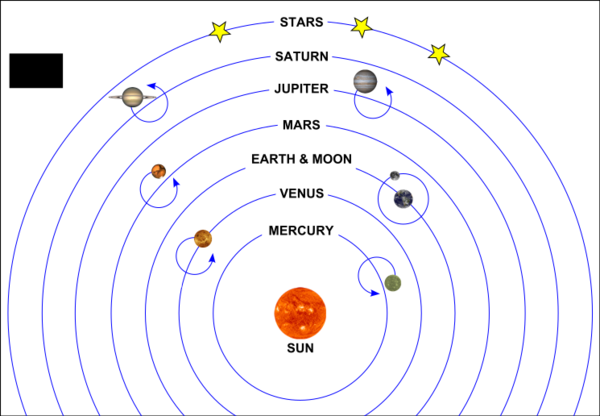
The necessity of epicycles in Copernicus' system is typically not depicted or mentioned in the school system. A comparison between Ptolemy's geocentric model of the universe (first) and Copernicus's heliocentric model (second) may be found below:
Ptolmy's Geocentric Model of the Universe
Copernicus' Heliocentric Model
Hence one sees what is meant by the two models said to have equal complexity. Not depicted are the 'epicycles upon epicycles' and other devices necessary for the systems.
Copernicus and Epicyles
Some assert that Copernicus ended up with even more epicycles than Ptolmy. From p.42 of a geocentric work Galileo Was Wrong its authors provide the following:
“ One of the more obvious faults of De revolutionibus was that for all its complaints against ancient epicycles, Copernicus actually produced more epicycles than Ptolemy! Ptolemy’s system has forty epicycles, whereas Copernicus ends up with forty-eight. Yet in the earlier work, the Commentariolus, Copernicus stated that his heliocentric system needed, only thirty-four epicycles, and even this numeration was off by four.86 What happened, of course, was that since the Commentariolus was merely a preliminary thesis, Copernicus soon discovered that when the time came to work out the finer details of his system a couple of decades later, he was forced to add fourteen more epicycles just to make his version of celestial mechanics come close to the accuracy of Ptolemy’s.87 As one source puts it: “...recent computer analyses...have shown the Copernican Prutenic Tables — so named because they were dedicated to the duke of Prussia — to have been scarcely more accurate.”88
More disturbing is the fact that, to make Ptolemy’s model appear worse than it really was, Copernicus exaggerated the number of epicycles employed by his ancient rival. Although Ptolemy used only forty epicycles, Copernicus asserted that he had eighty!89 This gives us a strong hint that Copernicus was not in this game merely to give the world a better model of cosmology; rather, he thought of it as an historic competition that allowed him to inflate his opponent’s errors. ”
Footnotes:
- 86 Copernicus writes in the Commentariolus: “Behold! Only 34 circles are required to explain the entire structure of the universe and the dance of the planets!” (Gingerich, The Book that Nobody Read, p. 56). But Koestler remarks: “incidentally, as Zinner has pointed out, even the famous count at the end of the Commentariolus is wrong as Copernicus forgot to account for the precession, the motions of the aphelia and the lunar nodes. Taking these into account, the Commentariolus uses thirty-eight not thirty- four circles," adding that Copernicus makes no mention of the total number of epicycles in De revolutionibus: “Apart from the erroneous reference to 34 epicycles, I have nowhere seen a count made of the number of circles in De revolutionibus” (The Sleepwalkers, p. 580), perhaps hiding the fact from his reader that it contained more epicycles than the De revolutionibus. Gingerich adds: “Copernicus must have realized that with his small epicyclets he actually had more circles than the Ptolemaic computational scheme used in the Alfonsine Tables or for the Stoeffler ephemerides" (op. cit., p. 58). Regarding the discrepancies among the orbits of Mars, Jupiter and Saturn in 1504, Gingerich writes: “...the evidence is firm that he had observed the cosmic dance at this time [1504] and was fully aware of the discrepancies in the tables. But what is most astonishing is that Copernicus never mentioned his observation, and his own tables made no improvement in tracking these conjunctions“ (ibid., p. 59).
- 87 The Sleepwalkers, p. 194-195. One reason Copernicus had so many epicycles is, rather than placing the sun in the center of the universe, he placed the Earth’s entire orbit in the center (although, according to Gingerich: “this was an unresolved mystery in the book, for Copernicus hedged on the issue,” The Book that Nobody Read, p. 163). Koestler remarks that discrepancies in the biographical literature on the number of epicycles in Copernicus’ system is due to the fact that most historians have not read Copernicus’ book but have depended on other biographers for their information. Koestler’s notes show that he did a painstaking analysis of De revolutionibus that allows him to conclude Copernicus used forty-eight epicycles (pp. 579-580). Gingerieh accounts for these extra epicycles as follows: “While he [Copernicus] had eliminated all of Ptolemy’s major epicycles, merging them all into the Earth's orbit, he then introduced a series of little epicyclets to replace the equant, one per planet” (The Book that Nobody Read, pp. 54-55). For mistaken scholarly accounts that settled on Copernicus having only 34 epicycles, Koestler cites the Chamber's Encyclopedia as stating the Copernican system reduced the epicycles “from eighty to thirty-four,” as is the case with Herbert Dingle’s address to the Royal Astronomical Society in 1943. In my research I found the same discrepancies. Ivars Peterson writes: “Copernicus needed more circles in his sun—centered model than Ptolemy did in his Earth-centered scheme [a] total of 34 circles for all the planets and the moon" (Newton's Clock: Chaos in the Solar System, New York: William H. Freeman and Co. 1993, p. 54). Some add even more epicycles to Copernicus, as is the case with James Burke: “To account for the apparent alterations in speed and movement of the planets, Copernicus was obliged to use as many as ninety Ptolemaic epicycles” (The Day the Universe Changed, p. 134).
- 88 Joshua Gilder and Anne-Lee Gilder, Heavenly Intrigue: Johannes Kepler, Tycho Brahe, and the Murder Behind One of History's Greatest Scientific Discoveries, New York: Doubleday, 2004, p. 38.
- 89 Owen Gingerich adds that the myth of having to put up with an inordinate amount of Ptolemaic epicycles perpetuated itself like an out-of-control gossip chain. He writes: “The legend reached its apotheosis when the 1969 Encyclopedia Britannica announced that, by the time of King Alfonso, each planet required 40 to 60 epicycles! The article concluded, ‘After surviving more than a millennium, the Ptolemaic system failed; its geometrical clockwork had become unbelievably cumbersome and without satisfactory improvements in its effectiveness.‘ When I challenged them, the Britannica editors replied lamely that the author of the article was no longer living, and they hadn’t the faintest idea if or where any evidence for the epicycles on epicycles could be found” (The Book that Nobody Read, pp. 56-57).
From Astronomy and History Selected Essays (Archive) by mathematician and historian of science Otto E. Neugebauer (bio) we read:
“ If one reads Copernicus only superficially and with the conviction that he had abolished, or at least greatly simplified, the Ptolemaic system, one will not be tempted to study the Almagest in any detail. Vieta [Franciscus Vieta, a French mathematician], of course, still knew better. He must have been fully aware of the fact that there was not a single proof or mathematical procedure in the De Revolutionibus which did not have its exact replica in the Almagest. To Vieta as one of the leaders in the new trend of mathematics it must have appeared rather antiquated when Copernicus again and again demonstrated by numerical computation that his model agreed with Ptolemy’s.
Modern historians, making ample use of the advantage of hindsight, stress the revolutionary significance of the heliocentric system and the simplifications it had introduced. In fact, the actual computation of planetary positions follows exactly the ancient pattern and the results are the same. The Copernican solar theory is definitely a step in the wrong direction for the actual computation as well as for the underlying cinematic concepts. The cinematically elegant idea of secondary epicycles for the lunar theory and as substitute for the equant as we now know, methods familiar to a school of Islamic astronomers—does not contribute to make the planetary phenomena easier to visualize. Had it not been for Tycho Brahe and Kepler, the Copernican system would have contributed to the perpetuation of the Ptolemaic system in a slightly more complicated form but more pleasing to philosophical minds. ”
Reception and Response
Bang to Eternity and Betwixt: Cosmos
By John Hussey (bio)
“ Despite the near universal acceptance today of the basic heliocentric idea (though not the epicycles or the circular orbits), Copernicus' theory was originally slow to catch on. Scholars hold that sixty years after the publication of The Revolutions there were only around 15 astronomers espousing Copernicanism in all of Europe: "Thomas Digges and Thomas Harriot in England; Giordano Bruno and Galileo Galilei in Italy; Diego Zuniga in Spain; Simon Stevin in the Low Countries; and in Germany, the largest group — Georg Joachim Rheticus, Michael Maestlin, Christoph Rothmann (who may have later recanted), and Johannes Kepler." Additional possibilities are Englishman William Gilbert, along with Achilles Gasser, Georg Vogelin, Valentin Otto, and Tiedemann Giese.
~
Only mild controversy (and no fierce sermons) was the immediate result of the 1543 publication of Copernicus‘ book. At the Council of Trent (1545—63) neither Copernicus' theory nor calendar reform (which would later use tables deduced from Copernicus' calculations) were discussed. It has been much debated why it was not until six decades after the publication of De revolutionibus that the Catholic Church took any official action against it, even the efforts of Tolosani going unheeded. Catholic side opposition only commenced seventy-three years later, when it was occasioned by Galileo.
The first notable to move against Copernicanism was the Magister of the Holy Palace (i.e., the Catholic Church's chief censor), Dominican Bartolomeo Spina, who "expressed a desire to stamp out the Copernican doctrine". But with Spina's death in 1546, his cause fell to his friend, the well known theologian-astronomer, the Dominican Giovanni Maria Tolosani of the Convent of St. Mark in Florence. Tolosani had written a treatise on reforming the calendar (in which astronomy would play a large role) and had attended the Fifth Lateran Council (1512-17) to discuss the matter. He had obtained a copy of De Revolutionibus in 1544. His denunciation of Copernicanism was written a year later, in 1545, in an appendix to his unpublished work, On the Truth of Sacred Scripture.
Emulating the rationalistic style of Thomas Aquinas, Tolosani sought to refute Copernicanism by philosophical argument. While still invoking Christian scripture and tradition, Tolosani strove to show that Copernicanism was absurd because it was unproven and unfounded. First, Copernicus had assumed the motion of the Earth but offered no physical theory whereby one would deduce this motion. (No one realized that the investigation into Copernicanism would result in a rethinking of the entire field of physics.) Second, Tolosani charged that Copernicus' thought process was backwards. He held that Copernicus had come up with his idea and then sought phenomena that would support it, rather than observing phenomena and deducing from them the idea of what caused them. In this, Tolosani was linking Copernicus' mathematical equations with the practices of the Pythagoreans (whom Aristotle had made arguments against, which were later picked up by Thomas Aquinas). It was argued that mathematical numbers were a mere product of the intellect without any physical reality, and as such "numbers could not provide physical causes in the investigation of nature." (This was basically a denial of the possibility of mathematical physics.)
Some astronomical hypotheses at the time (such as epicycles and eccentrics) were seen as mere mathematical devices to adjust calculations of where the heavenly bodies would appear, rather than an explanation of the cause of those motions. (As Copernicus still maintained the idea of perfectly spherical orbits, he relied on epicycles.) This "saving the phenomena" was seen as proof that astronomy and mathematics could not be taken as serious means to determine physical causes. Tolosani invoked this view in his final critique of Copernicus, saying that his biggest error was that he had started with "inferior" fields of science to make pronouncements about "superior“ fields. Copernicus had used mathematics and astronomy to postulate about physics and cosmology, rather than beginning with the accepted principles of physics and cosmology to determine things about astronomy and mathematics. Thus Copernicus seemed to be undermining the whole system of the philosophy of science at the time. Tolosani held that Copernicus had fallen into philosophical error because he had not been versed in physics and logic; anyone without such knowledge would make a poor astronomer and be unable to distinguish truth from falsehood. Because Copernicanism had not met the criteria for scientific truth set out by Thomas Aquinas, Tolosani held that it could only be viewed as a wild unproven theory. ”
Tychonic System
Put forward by Danish astronomer Tycho Brache in 1583, the Tychonic System of the solar system depicts a stationary round Earth with a Sun and Moon which revolve around it. Adopting benefits of the Copernican model, the planets revolve around the Sun, as the Sun revolves around the stationary Earth. With the Sun as center of planetary revolutions, the Tychonic model is said to have provided equivalent geometric explanations of the retrogrades for the stationary earth concept, and is known as a 'geoheliocentric' model.
Related: https://www.tychos.info - "The TYCHOS - Our Geoaxial Binary Solar System"
Johannes Kepler
Johannes Kepler, an assistant and later successor to Tycho Brache, was a heliocentrist who made contributions to the Solar System by making small improvements to Ptolmy's geocentric model of the orbits and epicycles and then applying those improvement to Copernicus' model of the orbits and epicycles, showing with more clarity that the planets move with a common relationship to the Sun.
The University of Texas depicts Kepler's contributions as follows:
http://farside.ph.utexas.edu/Books/Syntaxis/Almagest/node5.html
“ Johannes Kepler (1571-1630 CE) was fortunate enough to inherit an extensive set of naked-eye solar, lunar, and planetary angular position data from the Danish astronomer Tycho Brahe (1546-1601 CE). This data extended over many decades, and was of unprecedented accuracy.
Although Kepler adopted the heliocentric approach of Copernicus, what he effectively first did was to perfect Ptolemy's model of the solar system (or, rather, its heliocentric equivalent). Thus, Kepler replaced Ptolemy's erroneous equantless model of the sun's apparent orbit around the earth with a corrected version containing an equant--in the process, halving the eccentricity of the orbit (see Fig. 1). Kepler also introduced equants into the epicycles of the superior and inferior planets. Once he had perfected Ptolemy's model, the heliocentric nature of the solar system became manifestly apparent to Kepler. For instance, he found that the epicycles of the superior planets, the sun's apparent orbit around the earth, and the deferents of the inferior planets all have exactly the same eccentricity. The obvious implication is that these circles all correspond to some common motion within the solar system--in fact, the motion of the earth around the sun.
Once Kepler had corrected the Almagest model, he compared its predictions with his observational data. In particular, Kepler investigated the apparent motion of Mars in the night sky. Kepler found that his model performed extremely well, but that there remained small differences between its predictions and the observational data. The maximum discrepancy was about 8': i.e., about 1/4 the apparent size of the sun. By the standards of naked-eye astronomy, this was a very small discrepancy indeed. Nevertheless, given the incredible accuracy of Tycho Brahe's observations, it was still significant. Thus, Kepler embarked on an epic new series of calculations which eventually lead him to the conclusion that the planetary orbits are actually eccentric ellipses, rather than eccentric circles. Kepler published the results of his research in Astronomia Nova (New Astronomy) in 1609 CE. It is interesting to note that had Tycho's data been a little less accurate, or had the orbit of Mars been a little less eccentric, Kepler might well have settled for a model which was kinematically equivalent to a perfected version of the model described in the Almagest. We can also appreciate that, given the far less accurate observational data available to Ptolemy, there was no way in which he could have discerned the very small difference between elliptical planetary orbits and the eccentric circular orbits employed in the Almagest. ”
The above tells that by making slight corrections to the models of Ptolmy and Copernicus, Kepler found indirect evidence in the 'epicycles of the superior planets' and in the 'deferents of the inferior planets' supporting the idea that the planets moved with a common relationship to the Sun, in the form of common eccentricities of their orbits.
Elliptical Movement
Kepler also proposed that the orbits of the planets were elliptical rather than circular, which helped to reduce some epicycles. On the topic of Kepler's ellipses, Galileo Was Wrong says:
“ After Copernicus there were, of course, refinements, such as Johannes Kepler’s elliptical orbits of the planets, which seemed to make things run a bit more smoothly for the heliocentric system. Contrary to popular opinion, however, Kepler’s geometrical modification didn’t prove Copernicus was right. It merely revealed Kepler’s preferences, since he knew that, if the same elliptical modifications were made to the reigning geocentric model of Tycho Brahe, or even to Ptolemy’s model, they would have shown heliocentrism to be merely an alternative system, not a superior one. As one physics course puts it: “However, one could also construct a ‘Tychonean’ model with elliptical orbits.”116 In fact, it is well known among historians that although Kepler claimed the discovery of elliptical orbits was supported by independent computations of planetary positions, in actuality he employed the elliptical theory in order to derive his “observations.”117 Be that as it may, the ellipses merely helped both the heliocentric and geocentric models to resolve that planetary orbits were not necessarily perfect circles, as opposed to Aristotle’s “crystalline spheres” (although some are very close to perfect circles). 118
Even after Kepler’s modifications, anomalies regarding the motions of the heavenly bodies remained, and stubbornly so. Although geometrically speaking the orbits are not perfect circles, they are not perfect ellipses either, but precess at different rates and contain various eccentricities. Quoting Hoyle again:
- "The planetary orbits are not strictly ellipses, as we have so far taken them to be, because one planet disturbs the order of another through the gravitational force that it exerts... In all cases the orbits are nearly circles....lt is curious that although the actual orbits do not differ in shape much from circles the errors of a circular model can nevertheless be quite large. Indeed, errors as large as this were quite unacceptable to Greek astronomers of the stature of Hipparchus and Ptolemy. It was this, rather than prejudice, which caused them to reject the simply heliocentric theory of Aristarehus... The Hipparchus theory grapples with the facts whereas the circular picture of Aristarehus fails to do so.... The theory of Ptolemy, a few minor imperfections apart, worked correctly to the first order in explaining the planetary eccentricities. Copernicus with his heliocentric theory had to do at least as well as this, which meant that he had to produce something much better than the simple heliocentric picture of Aristarehus... Kepler achieved improvements, but not complete success, and always at the expense of increasing complexity. Kepler and his successors might well have gone on in this style for generations without arriving at a satisfactory final solution, for a reason we now understand clearly. There is no simple mathematical expression for the way in which the direction of a planet — its heliocentric longitude — changes with time. Even today we must express the longitude as an infinite series of terms when we use time as the free variable. What Ptolemy, Copernicus, and Kepler, in his early long calculations, were trying to do was to discover by trial and error the terms of this series. Since the terms become more complicated as one goes to higher orders in the eccentricity, the task became successively harder and harder..." 119 ”
Approximations
On p.129 of Gravitation Vs. Relativity its author Charles Lane Poor, Professor of Celestial Mechanics at Columbia University, tells us that Kepler's Laws provide only approximations for the places of the planets:
“ From the time of Newton, it has been known that Kepler’s laws are mere approximations, computer’s fictions handy mathematical devices for finding the approximate place of a planet in the heavens. They apply with greater accuracy to some planets than to others. Jupiter and Saturn show the greatest deviations from strictly elliptical motion. The latter body is often nearly a degree away from the place it would have been had its motion about the sun been strictly in accord with Kepler’s laws. This is such a large discrepancy that it can be detected by the unaided eye. The moon is approximately half a degree in diameter, so that the discrepancy in the motion of Saturn is about twice the apparent diameter of the moon. In a single year, during the course of one revolution about the sun, the Earth may depart from the theoretical ellipse by an amount sufficient to appreciably change the apparent place of the sun in the heavens. ”
Modern Heliocentrism
Prediction in modern heliocentrism is still performed through patterns. By analysis of historic tables it is possible to construct functions which can predict where a planet will be in the future. This is how prediction in astronomy has been performed since times of antiquity, and how it is performed today. Indeed, modern astronomers still use epicycles—now called perturbations—to predict the location of planets.
See: Astronomical Prediction Based on Patterns
Quotes on Earth's Movement
“ There is no planetary observation by which we on Earth can prove that the Earth is moving in an orbit around the sun. Thus all Galileo’s discoveries with the telescope can be accommodated to the system invented by Tycho Brahe just before Galileo began his observations of the heavens. In this Tychonic system, the planets Mercury, Venus, Mars, Jupiter, and Saturn move in orbits around the sun, while the sun moves in an orbit around the Earth in a year. Furthermore, the daily rotation of the heavens is communicated to the sun and planets, so that the Earth itself neither rotates nor revolves in an orbit. ”
—Physicist I. Bernard Cohen, Birth of a New Physics, revised and updated, New York: W. W. Norton, 1985, p.78.
“ Whether the Earth rotates once a day from west to cast, as Copenricus taught, or the heavens revolve once a day from east to west, as his predecessors believed, the observable phenomena will be exactly the same. This shows a defect in Newtonian dynamics, since an empirical science ought not to contain a metaphysical assumption, which can never be proved or disproved by observation. ”
—Philosopher and Mathematician Bertrand Russell, Quoted from Dennis W. Sciama’s, The Unity of the Universe, New York: Doubleday, 1961, p. 102-103.
“ We know that the difference between a heliocentric theory and a geocentric theory is one of relative motion only, and that such a difference has no physical significance. ”
—Astronomer Sir Fred Hoyle
“ People need to be aware that there is a range of models that could explain the observations. For instance, I can construct you a spherically symmetrical universe with Earth at its center, and you cannot disprove it based on observations. You can only exclude it on philosophical grounds. In my view there is absolutely nothing wrong in that. What I want to bring into the open is the fact that we are using philosophical criteria in choosing our models. A lot of cosmology tries to hide that. ”
—Cosmologist George Ellis in Scientific American, "Thinking Globally, Acting Universally", October 1995
Topics
Round Earth Topics
- Discovery of Neptune - A claim that Neptune was discovered through mathematics alone
- Precession of Mercury's Orbit - Einstein's use of Mercury as evidence of Relativity
Flat Earth Topics
- Kings Dethroned - A text questioning astronomical triangulation methods
- Astronomical Prediction Based on Patterns - Epicycles are still used for astronomical prediction
- Three Body Problem - The heliocentric Sun-Earth-Moon system cannot be simulated