Difference between revisions of "Three Body Problem"
Tom Bishop (talk | contribs) |
Tom Bishop (talk | contribs) |
||
| (25 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | The '''Three Body Problem''' is a four hundred year old problem of mathematics which has its roots in the unsuccessful attempts to simulate a heliocentric Sun-Earth-Moon system | + | The '''Three Body Problem''' is a four hundred year old problem of mathematics which has its roots in the unsuccessful attempts to simulate a heliocentric Sun-Earth-Moon system. |
| − | Due to the nature of Newtonian Gravity, a three body system inherently prefers to be a two body orbit and will attempt to kick out the smallest body from the system—often causing the system to be destroyed altogether. There are a limited range of scenarios in which three body orbits may exist<sup>[https://wiki.tfes.org/Three_Body_Problem#A_Thousand_New_Solutions]</sup>. It is seen that those configurations require at least two of the three bodies to be of the same mass, can only exist with specific magnitudes in specific, sensitive, and highly symmetrical configurations, and exhibit odd loopy orbits that look quite different than the systems of astronomy proposed by Copernicus. The slightest imperfection, such as with bodies of different masses, or the effect of a gravitational influence external to the system, causes a chain reaction of random chaos which compels the entire system to fall apart<sup>[https://wiki.tfes.org/Three_Body_Problem#Chaos_Theory:_A_Demo]</sup>. | + | Due to the nature of Newtonian Gravity, a three body system inherently prefers to be a two body orbit and will attempt to kick out the smallest body from the system—often causing the system to be destroyed altogether.<sup>[https://wiki.tfes.org/Symplectic_Integrators#Sun-Earth-Moon_System]</sup> There are a limited range of scenarios in which three body orbits may exist<sup>[https://wiki.tfes.org/Three_Body_Problem#A_Thousand_New_Solutions]</sup>. It is seen that those configurations require at least two of the three bodies to be of the same mass, can only exist with specific magnitudes in specific, sensitive, and highly symmetrical configurations, and exhibit odd loopy orbits that look quite different than the systems of astronomy proposed by Copernicus. The slightest imperfection, such as with bodies of different masses, non-symmetrical spacing, or the effect of a gravitational influence external to the system, causes a chain reaction of random chaos which compels the entire system to fall apart<sup>[https://wiki.tfes.org/Three_Body_Problem#Chaos_Theory:_A_Demo]</sup>. |
{{cite|Describing the motion of any planetary system (including purely imaginary ones that exist only on paper) is the subject of a branch of mathematics called celestial mechanics. Its problems are extremely difficult and have eluded the greatest mathematicians in history.}} —Paul Trow, [https://web.archive.org/web/20190405003722/http://ptrow.com/articles/ChaosandSolarSystem5.htm ''Chaos and the Solar System''] | {{cite|Describing the motion of any planetary system (including purely imaginary ones that exist only on paper) is the subject of a branch of mathematics called celestial mechanics. Its problems are extremely difficult and have eluded the greatest mathematicians in history.}} —Paul Trow, [https://web.archive.org/web/20190405003722/http://ptrow.com/articles/ChaosandSolarSystem5.htm ''Chaos and the Solar System''] | ||
| Line 19: | Line 19: | ||
==NOVA Documentary== | ==NOVA Documentary== | ||
| − | A Nova documentary, ''The Strange New Science of Chaos'', states that | + | A Nova documentary, ''The Strange New Science of Chaos'', states that mathematicians were unable to extend Newton's model beyond two bodies. See from 9:40 to 13:20 (~4m): |
| − | {{#ev:youtube|https:// | + | {{#ev:youtube|https://www.youtube.com/watch?v=YSugrPBR9JA|||||start=582&end=814&loop=1}} |
==Newton's Solution== | ==Newton's Solution== | ||
| Line 168: | Line 168: | ||
[[File:Three_body_sim.png|350px|link=https://cloud.anylogic.com/model/f1999d97-8de2-4804-9940-5ae261d7ad86?mode=SETTINGS&tab=GENERAL]] | [[File:Three_body_sim.png|350px|link=https://cloud.anylogic.com/model/f1999d97-8de2-4804-9940-5ae261d7ad86?mode=SETTINGS&tab=GENERAL]] | ||
| − | Adjust the slider values in the upper left of the simulation to something very slight to find what happens. What you will see is a demonstration of Chaos Theory. Any slight modification to a perfect system creates a chain reaction of random chaos. | + | Adjust the mass slider values in the upper left of the simulation to something very slight to find what happens. What you will see is a demonstration of Chaos Theory. Any slight modification to a perfect system creates a chain reaction of random chaos. |
This is precisely the issue of modeling the Heliocentric System, and why its fundamental system cannot exist. Only very specific, sensitive, and highly symmetrical configurations may exist. The slightest deviation, such as with a system with unequal masses, or the minute influence from a gravitating body external to the system, will cause the entire system to fly apart. The reader is invited to decide for his or her own self whether those scenarios would occur in nature as described by popular theory. | This is precisely the issue of modeling the Heliocentric System, and why its fundamental system cannot exist. Only very specific, sensitive, and highly symmetrical configurations may exist. The slightest deviation, such as with a system with unequal masses, or the minute influence from a gravitating body external to the system, will cause the entire system to fly apart. The reader is invited to decide for his or her own self whether those scenarios would occur in nature as described by popular theory. | ||
| Line 250: | Line 250: | ||
Despite any fanciful allusions that the choice is between either "destabilizing the orbits with massive errors" or "waiting for Sun to evolve," and reassurances that our solar system is stable despite the inability of simulating it—all common statements to excuse away the problems of simulating bodies in heliocentric orbits—its developers freely admit that the program is not using a full simulation of gravity. The article states "By default, the simulations in Universe Sandbox ² try to set an accuracy which prevents orbits from falling apart due to error". | Despite any fanciful allusions that the choice is between either "destabilizing the orbits with massive errors" or "waiting for Sun to evolve," and reassurances that our solar system is stable despite the inability of simulating it—all common statements to excuse away the problems of simulating bodies in heliocentric orbits—its developers freely admit that the program is not using a full simulation of gravity. The article states "By default, the simulations in Universe Sandbox ² try to set an accuracy which prevents orbits from falling apart due to error". | ||
| − | == | + | ==Symmetrical Simulations== |
| − | + | The simulations are highly symmetrical with mass restrictions: | |
| − | |||
| − | |||
| − | |||
| − | The | ||
===Over a Thousand New Solutions - New Scientist=== | ===Over a Thousand New Solutions - New Scientist=== | ||
| Line 275: | Line 271: | ||
:''FIG. 1. (color online.) Brief overview of the six newly-found families of periodic three-body orbits.'' | :''FIG. 1. (color online.) Brief overview of the six newly-found families of periodic three-body orbits.'' | ||
| − | |||
| − | |||
| − | |||
| − | |||
===Over 600 New Orbits=== | ===Over 600 New Orbits=== | ||
| Line 286: | Line 278: | ||
:[[File:47-scientistsdi.jpg|400px]] | :[[File:47-scientistsdi.jpg|400px]] | ||
| − | :{{cite|These 695 periodic orbits include the well-known figure-eight family found by Moore in 1993, the 11 families found by Suvakov and Dmitrasinovic in 2013, and more than 600 new families reported for the first time | + | :{{cite|These 695 periodic orbits include the well-known figure-eight family found by Moore in 1993, the 11 families found by Suvakov and Dmitrasinovic in 2013, and more than 600 new families reported for the first time.}} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Quotes== | ==Quotes== | ||
| Line 320: | Line 292: | ||
Physcist David Gozzard ([https://equs.org/users/dr-david-gozzard bio]) says in his video ''[https://www.youtube.com/watch?v=eqSPvyaxMI8 Weird Orbits - the three body problem]'' (Runtime - 4m): | Physcist David Gozzard ([https://equs.org/users/dr-david-gozzard bio]) says in his video ''[https://www.youtube.com/watch?v=eqSPvyaxMI8 Weird Orbits - the three body problem]'' (Runtime - 4m): | ||
| − | {{cite|Three hundred and fifty years ago Isaac Newton formulated his theory of gravity Newton's theory unified the heavens and the earth under the same physical laws and neatly explained the orbits of the planets, the motion of comets, and how the moon causes the tides. Although Einstein's general relativity has supplanted Newton's theory as a better model of gravity, Newtonian mechanics got us to the moon and are still used to calculate the trajectories of spacecraft throughout the solar system. In spite of this success and more than three centuries of progress we still do not have a neat set of equations that allow us to calculate the orbital parameters of more than two objects at once. This is called the three-body problem, or more generally the n-body problem. | + | {{cite|Three hundred and fifty years ago Isaac Newton formulated his theory of gravity Newton's theory unified the heavens and the earth under the same physical laws and neatly explained the orbits of the planets, the motion of comets, and how the moon causes the tides. Although Einstein's general relativity has supplanted Newton's theory as a better model of gravity, Newtonian mechanics got us to the moon and are still used to calculate the trajectories of spacecraft throughout the solar system. In spite of this success and more than three centuries of progress we still do not have a neat set of equations that allow us to calculate the orbital parameters of more than two objects at once. This is called the three-body problem, or more generally the n-body problem.}} |
===Paul Nahin=== | ===Paul Nahin=== | ||
| Line 326: | Line 298: | ||
From [https://books.google.com/books?id=pxz8G-KF3ZgC&lpg=PA132&ots=YuiY4cAEs_&pg=PA132#v=onepage&f=false p.132 of ''Number-Crunching''] by Dr. Paul J. Nahin ([https://en.wikipedia.org/wiki/Paul_J._Nahin bio]): | From [https://books.google.com/books?id=pxz8G-KF3ZgC&lpg=PA132&ots=YuiY4cAEs_&pg=PA132#v=onepage&f=false p.132 of ''Number-Crunching''] by Dr. Paul J. Nahin ([https://en.wikipedia.org/wiki/Paul_J._Nahin bio]): | ||
| − | {{cite|The study of how three massive bodies gravitationally interact is called the three-body problem, and its general solution eluded even the genius of Newton. But, of course, that didn’t mean it was necessarily an impossible problem, just that it was a very, very difficult problem. Perhaps, it was hoped, with advancing technical knowledge and the appearance of an even greater intellect than Newton’s, the three-body problem could be solved. That lure, of being the one that finally did what the great Newton could not, attracted some of the most brilliant analysts over the next 250 years. Such luminaries as the Swiss Leonhard Euler (1707-1783), the French Joseph Lagrange (1736-1813), and the German Carl Jacobi (1804-1851), for example, all | + | {{cite|The study of how three massive bodies gravitationally interact is called the three-body problem, and its general solution eluded even the genius of Newton. But, of course, that didn’t mean it was necessarily an impossible problem, just that it was a very, very difficult problem. Perhaps, it was hoped, with advancing technical knowledge and the appearance of an even greater intellect than Newton’s, the three-body problem could be solved. That lure, of being the one that finally did what the great Newton could not, attracted some of the most brilliant analysts over the next 250 years. Such luminaries as the Swiss Leonhard Euler (1707-1783), the French Joseph Lagrange (1736-1813), and the German Carl Jacobi (1804-1851), for example, all tried their hands at it, but except for limited partial successes made under special, restrictive assumptions, the general solution of the three-body problem defeated every one of them.}} |
===Vinay Ambegaokar=== | ===Vinay Ambegaokar=== | ||
| Line 336: | Line 308: | ||
===Isaac Newton=== | ===Isaac Newton=== | ||
| − | On [https://books.google.com/books?id=Z0VvDwAAQBAJ&lpg=PA174&pg=PA174#v=onepage&q&f=false p.174 of ''Medical Reasoning: The Nature and Use of Medical Knowledge''] ([https://web.archive.org/web/20191024231709/https://books.google.com/books?id=Z0VvDwAAQBAJ&lpg=PA174&pg=PA174#v=onepage&q&f=false Archive]) its author | + | On [https://books.google.com/books?id=Z0VvDwAAQBAJ&lpg=PA174&pg=PA174#v=onepage&q&f=false p.174 of ''Medical Reasoning: The Nature and Use of Medical Knowledge''] ([https://web.archive.org/web/20191024231709/https://books.google.com/books?id=Z0VvDwAAQBAJ&lpg=PA174&pg=PA174#v=onepage&q&f=false Archive]) its author Erwin B. Montgomery shares this quote from Newton: |
| − | {{cite|An example of a system that can be described explicitly by a mathematical metaphor proved unsolvable (at least explicitly in algebraic or integral functions) is the three-body problem, such as the orbits of the earth, moon, and sun when all three are considered simultaneously. While the two-body problem is solvable, such as the orbits of the earth and moon, even Newton recognized the difficulty and indeed potential intractability of the three-body problem, commenting in 1684 that “to define these motions by exact laws admitting of easy calculation exceeds, if I am not mistaken, the force of any human mind” (from a draft of De | + | {{cite|An example of a system that can be described explicitly by a mathematical metaphor proved unsolvable (at least explicitly in algebraic or integral functions) is the three-body problem, such as the orbits of the earth, moon, and sun when all three are considered simultaneously. While the two-body problem is solvable, such as the orbits of the earth and moon, even Newton recognized the difficulty and indeed potential intractability of the three-body problem, commenting in 1684 that “to define these motions by exact laws admitting of easy calculation exceeds, if I am not mistaken, the force of any human mind” (from a draft of De Motu, tentatively dated in December 1684; Wilson 1989).}} |
===Martin Gutzwiller=== | ===Martin Gutzwiller=== | ||
| − | The end section of a paper titled ''[http://sites.apam.columbia.edu/courses/ap1601y/Moon-Earth-Sin%20RMP.70.589.pdf Moon-Earth-Sun: The oldest three-body problem]'' by physicist Martin C. Gutzwiller ([https://en.wikipedia.org/wiki/Martin_Gutzwiller bio]) concludes that Newton's laws are not a sufficient explanation: | + | The end section of a paper titled ''[http://sites.apam.columbia.edu/courses/ap1601y/Moon-Earth-Sin%20RMP.70.589.pdf Moon-Earth-Sun: The oldest three-body problem]'' ([https://web.archive.org/web/20160622205656/http://sites.apam.columbia.edu/courses/ap1601y/Moon-Earth-Sin%20RMP.70.589.pdf Archive]) by physicist Martin C. Gutzwiller ([https://en.wikipedia.org/wiki/Martin_Gutzwiller bio]) concludes that Newton's laws are not a sufficient explanation: |
{{cite|The three-body problem teaches us a sobering lesson about our ability to comprehend the outside world in terms of a few basic mathematical relations. Many physicists, maybe early in their careers, had hopes of coordinating their field of interest, if not all of physics, into some overall rational scheme. The more complicated situations could then be reduced to some simpler models in which all phenomena would find their explanation. This ideal goal of the scientific enterprise has been promoted by many distinguished scientists [see Weinberg’s (1992) Dream of a Final Theory, with a chapter ‘‘Two Cheers for Reductionism’’]....Many physicists may be tempted to see in Newton’s equations of motion and his universal gravitation a sufficient explanation for the three-body problem, with the details to be worked out by the technicians. But even a close look at the differential equations (29) and (30) does not prepare us for the idiosyncracies of the lunar motion, nor does it help us to understand the orbits of asteroids in the combined gravitational field of the Sun and Jupiter.}} | {{cite|The three-body problem teaches us a sobering lesson about our ability to comprehend the outside world in terms of a few basic mathematical relations. Many physicists, maybe early in their careers, had hopes of coordinating their field of interest, if not all of physics, into some overall rational scheme. The more complicated situations could then be reduced to some simpler models in which all phenomena would find their explanation. This ideal goal of the scientific enterprise has been promoted by many distinguished scientists [see Weinberg’s (1992) Dream of a Final Theory, with a chapter ‘‘Two Cheers for Reductionism’’]....Many physicists may be tempted to see in Newton’s equations of motion and his universal gravitation a sufficient explanation for the three-body problem, with the details to be worked out by the technicians. But even a close look at the differential equations (29) and (30) does not prepare us for the idiosyncracies of the lunar motion, nor does it help us to understand the orbits of asteroids in the combined gravitational field of the Sun and Jupiter.}} | ||
| Line 370: | Line 342: | ||
{{cite|In the early 19th century, building on earlier work of Lagrange, <sup>12</sup> Laplace ‘proved’ the stability of the solar system, and although this work was an important step and is mathematically correct as far as it goes, it was soon recognized that he had not shown stability for the ''n'' body problem, but rather for an attenuated version of it in which higher-order interactions between planets are ignored. Such claims and half-successes by the mathematical giants of the ages (and many other less-than-giants) of course only added celebrity to the ''n'' body problem, and to the stability problem in particular.}} | {{cite|In the early 19th century, building on earlier work of Lagrange, <sup>12</sup> Laplace ‘proved’ the stability of the solar system, and although this work was an important step and is mathematically correct as far as it goes, it was soon recognized that he had not shown stability for the ''n'' body problem, but rather for an attenuated version of it in which higher-order interactions between planets are ignored. Such claims and half-successes by the mathematical giants of the ages (and many other less-than-giants) of course only added celebrity to the ''n'' body problem, and to the stability problem in particular.}} | ||
| − | Later researchers went on to 'simulate' the solar system with geometry preserving schemes. See '''[[Symplectic Integrators]]''' | + | Later researchers went on to 'simulate' the solar system with two body approximation and geometry preserving schemes. See the pages '''[[Numerical Solutions]]''' and '''[[Symplectic Integrators]]'''. |
==N-Body Symmetry== | ==N-Body Symmetry== | ||
| Line 383: | Line 355: | ||
*'''[[Three Body Problem]]''' - The heliocentric Sun-Earth-Moon system cannot be simulated | *'''[[Three Body Problem]]''' - The heliocentric Sun-Earth-Moon system cannot be simulated | ||
| + | :*'''[[Numerical Solutions]]''' - The available solutions for celestial systems do not fully simulate gravity | ||
:*'''[https://wiki.tfes.org/Astronomical_Prediction_Based_on_Patterns Perturbation Methods]''' - Epicycles are still used for astronomical prediction | :*'''[https://wiki.tfes.org/Astronomical_Prediction_Based_on_Patterns Perturbation Methods]''' - Epicycles are still used for astronomical prediction | ||
:*'''[https://wiki.tfes.org/Astronomical_Prediction_Based_on_Patterns#The_Eclipses Eclipse Prediction]''' - The eclipses are predicted with cycles and patterns | :*'''[https://wiki.tfes.org/Astronomical_Prediction_Based_on_Patterns#The_Eclipses Eclipse Prediction]''' - The eclipses are predicted with cycles and patterns | ||
Revision as of 08:17, 24 June 2021
The Three Body Problem is a four hundred year old problem of mathematics which has its roots in the unsuccessful attempts to simulate a heliocentric Sun-Earth-Moon system.
Due to the nature of Newtonian Gravity, a three body system inherently prefers to be a two body orbit and will attempt to kick out the smallest body from the system—often causing the system to be destroyed altogether.[1] There are a limited range of scenarios in which three body orbits may exist[2]. It is seen that those configurations require at least two of the three bodies to be of the same mass, can only exist with specific magnitudes in specific, sensitive, and highly symmetrical configurations, and exhibit odd loopy orbits that look quite different than the systems of astronomy proposed by Copernicus. The slightest imperfection, such as with bodies of different masses, non-symmetrical spacing, or the effect of a gravitational influence external to the system, causes a chain reaction of random chaos which compels the entire system to fall apart[3].
“ Describing the motion of any planetary system (including purely imaginary ones that exist only on paper) is the subject of a branch of mathematics called celestial mechanics. Its problems are extremely difficult and have eluded the greatest mathematicians in history. ” —Paul Trow, Chaos and the Solar System
400 Years of Defiance
In The Physics Problem that Isaac Newton Couldn't Solve (Archive) physics and astronomy professor Robert Scherrer (bio) tells us:
“ There's a physics problem so difficult, so intractable, that even Isaac Newton, undoubtedly the greatest physicist who ever lived, couldn't solve it. And it's defied everyone else's attempts ever since then.
This is the famous three-body problem. When Newton invented his theory of gravity, he immediately set to work applying it to the motions of the planets in the solar system. If you have a planet orbiting a much larger body, like the sun, and the orbit is circular, then the problem is easy to solve -- it's something that's done in a high school physics class.
But a circular orbit isn't the most general possibility, and sometimes one body isn't much smaller than the object it orbits (think of the Moon going around the Earth). This more complicated case can still be solved -- Newton showed that the two bodies orbit their common center of mass in elliptical orbits. In fact, this prediction of elliptical orbits really cemented the case for Newton's theory of gravity. The calculation is a lot trickier than for circular orbits, but we still throw it at undergraduate physics majors in their second or third year.
Now add a third body, and everything falls apart. The problem goes from one that a smart undergraduate can tackle to one that has defied solution for 400 years. ”
NOVA Documentary
A Nova documentary, The Strange New Science of Chaos, states that mathematicians were unable to extend Newton's model beyond two bodies. See from 9:40 to 13:20 (~4m):
Newton's Solution
Mathematician and astronomer Issac Newton is credited to have "brought the laws of physics to the solar system."1 To solve the multi-body problems of his system Newton famously invoked divine intervention (Archive):
“ At the beginning of the 18th century, Newton famously wrote that the solar system needed occasional divine intervention (presumably a nudge here and there from the hand of God) in order to remain stable.11 This was interpreted to mean that Newton believed his mathematical model of the solar system—the n body problem—did not have stable solutions. Thus was the gauntlet laid down, and a proof of the stability of the n body problem became one of the great mathematical challenges of the age.
- 11Newton's remarks about divine intervention appear in Query 23 of the 1706 (Latin) edition of Opticks, which became Query 31 of the 1717 (2nd Edition) edition see Quote Q[New] in Appendix E). Similar 'theological' remarks are found in scholia of the 2nd and 3rd editions of Principia, and in at least one of Newton's letters. In a 1715 letter to Caroline, Princess of Wales, Leibniz observed sarcastically that Newton had not only cast the Creator as a clock-maker, and a faulty one, but now as a clock-repairman (see [Klo73], Part XXXIV, pp. 54-55). ”
- 1The University of California San Diego credits Newton with providing the laws of physics for the Solar System (Archive):
- “ Then came Isaac Newton (1642-1727) who brought the laws of physics to the solar system. Isaac Newton explained why the planets move the way they do, by applying his laws of motion, and the force of gravitation between any two bodies, letting the force decrease with the square of the distance between the two bodies. ”
Henri Poincaré
Caltech physicist Sean Carrol (bio) gives a history of the problem on his page N-Bodies:
“ The N-body problem is one of the most famous, and easily stated, problems in mathematical physics: find exact solutions to point masses moving under their mutual Newtonian gravitational forces (i.e. the inverse-square law). For N=2 the complete set of solutions is straightforward and has been known for a long time — each body moves in a conic section (circle, ellipse, parabola or hyperbola) around the center of mass. In fact, Kepler found the solution even before Newton came up with the problem!
But let N=3 and chaos breaks loose, quite literally. For a long time people recognized that the motion of three gravitating bodies would be a difficult problem, but there were hopes to at least characterize the kinds of solutions that might exist (even if we couldn’t write down the solutions explicitly). It became a celebrated goal for mathematical physicists, and the very amusing story behind how it was resolved is related in Peter Galison’s book Einstein’s Clocks and Poincare’s Maps. In 1885, a mathematical competition was announced in honor of the 60th birthday of King Oscar II of Sweden, and the three-body problem was one of the questions. (Feel free to muse about the likelihood of the birthday of any contemporary world leader being celebrated by mathematical competitions.) Henri Poincare was a favorite to win the prize, and he submitted an essay that demonstrated the stability of planetary motions in the three-body problem (actually the “restricted” problem, in which one test body moves in the gravitational field generated by two others). In other words, without knowing the exact solutions, we could at least be confident that the orbits wouldn’t go crazy; more technically, solutions starting with very similar initial conditions would give very similar orbits. Poincare’s work was hailed as brilliant, and he was awarded the prize.
But as his essay was being prepared for publication in Acta Mathematica, a couple of tiny problems were pointed out by Edvard Phragmen, a Swedish mathematician who was an assistant editor at the journal. Gosta Mittag-Leffler, chief editor, forwarded Phragmen’s questions to Poincare, asking him to fix up these nagging issues before the prize essay appeared in print. Poincare went to work, but discovered to his consternation that one of the tiny problems was in fact a profoundly devastating possibility that he hadn’t really taken seriously. What he ended up proving was the opposite of his original claim — three-body orbits were not stable at all. Not only were orbits not periodic, they didn’t even approach some sort of asymptotic fixed points.
Now that we have computers to run simulations, this kind of behavior is less surprising (example here from Steve McMillan — note how the final “binary” is not made of the same “stars” as the original one), but at the time it came as an utter shock. In his attempt to prove the stability of planetary orbits, Poincare ended up inventing chaos theory.
But the story doesn’t quite end there. Mittag-Leffler, convinced that Poincare would be able to tie up the loose threads in his prize essay, went ahead and printed it. By the time he heard from Poincare that no such tying-up would be forthcoming, the journal had already been mailed to mathematicians throughout Europe. Mittag-Leffler swung into action, telegraphing Berlin and Paris in an attempt to have all copies of the journal destroyed. He basically succeeded, but not without creating a minor scandal in elite mathematical circles across the Continent. (The Wikipedia entry on Poincare tells a much less interesting, and less accurate, version of the story.)
However, just because the general solution to the three-body (and more-body) problem is chaotic, doesn’t mean we can’t find special exact solutions in highly-symmetric conditions, and that’s just what Cris Moore and Michael Nauenberg have recently been doing. The image at the top really is an exact solution to twenty-one equal-mass objects moving in a figure-eight under their mutual gravitational attraction. They’re moving in a plane, of course, but that’s not strictly necessary; here’s a close relative of the figure-8, perturbed outside the plane. ”
“ From there you can just go nuts; here’s an example with twelve objects orbiting with cubic symmetry — four distinct periodic paths with three particles each. ”
Sean Carrol describes the three body problem orbits as chaotic and classifies the special orbits which were discovered as "highly-symmetric." Dr. Carrol proceeds to give animations of figure eight configurations and other special symmetrical orbits which have been discovered.
Readers should decide for themselves whether the Sun-Earth-Moon system or other systems proposed by contemporary Astronomy are "highly symmetric" systems.
Ask a Mathematician
https://www.askamathematician.com/2011/10/q-what-is-the-three-body-problem/ (Archive)
“ Q: What is the three body problem?
Physicist: The three body problem is to exactly solve for the motions of three (or more) bodies interacting through an inverse square force (which includes gravitational and electrical attraction).
The problem with the 3-body problem is that it can’t be done, except in a very small set of frankly goofy scenarios (like identical planets following identical orbits). ”
No General Solutions
Physics Professor Richard Fitzpatrick at the University of Texas says (Archive):
“ We saw earlier, in Section 2.9, that an isolated dynamical system consisting of two freely moving point masses exerting forces on one another--which is usually referred to as a two-body problem--can always be converted into an equivalent one-body problem. In particular, this implies that we can exactly solve a dynamical system containing two gravitationally interacting point masses, because the equivalent one-body problem is exactly soluble. (See Sections 2.9 and 4.16.) What about a system containing three gravitationally interacting point masses? Despite hundreds of years of research, no useful general solution of this famous problem--which is usually called the three-body problem--has ever been found. ”
Science China Press says (Archive):
“ In general, orbits described by the three-body problem are non-periodic, i.e. chaotic, and are rather sensitive to initial conditions. According to the theory of chaos, uncertainty in initial conditions enlarges exponentially for chaotic dynamic systems. Therefore, it is rather difficult to gain reliable convergent numerical simulations of chaotic orbits of three-body systems across a long interval of time. Due to this, it is also difficult to find periodic orbits of three-body systems by means of numerical methods. ”
From The Three-Body Problem (Archive) by Z.E. Musielak and B. Quarles we see:
“ In the three-body problem, three bodies move in space under their mutual gravitational interactions as described by Newton’s theory of gravity. Solutions of this problem require that future and past motions of the bodies be uniquely determined based solely on their present positions and velocities. In general, the motions of the bodies take place in three dimensions (3D), and there are no restrictions on their masses nor on the initial conditions. Thus, we refer to this as the general three-body problem . At first glance, the difficulty of the problem is not obvious, especially when considering that the two-body problem has well-known closed form solutions given in terms of elementary functions. Adding one extra body makes the problem too complicated to obtain similar types of solutions. In the past, many physicists, astronomers and mathematicians attempted unsuccessfully to find closed form solutions to the three-body problem. Such solutions do not exist because motions of the three bodies are in general unpredictable, which makes the three-body problem one of the most challenging problems in the history of science. ”
As we read above, there are no general solutions to the Three Body Problem and that the motions are unpredictable. As Sean Carroll and the authors of "Ask A Mathematician" related, the only solutions require very specific and odd scenarios.
A Thousand New Solutions
In 2017 researchers used a supercomputer to test various configurations and reported over one thousand new special solutions to the Three Body Problem. We read an account from a New Scientist article titled Infamous three-body problem has over a thousand new solutions (Archive) :
“ For more than 300 years, mathematicians have puzzled over the three-body problem – the question of how three objects orbit one another according to Newton’s laws. Now, there are 1223 new solutions to the conundrum, more than doubling the current number of possibilities.
No single equation can predict how three bodies will move in relation to one another and whether their orbits will repeat or devolve into chaos. Mathematicians must test each specific scenario to see if the objects will stay bound in orbit or be flung away.
The new solutions were found when researchers at Shanghai Jiaotong University in China tested 16 million different orbits using a supercomputer.
All the fresh orbits found are periodic. This means that each object, whether it’s a planet or a proton, ends up where it first began its orbit, with their paths forming three intertwined, closed loops.
“It is impressive that they’ve made the list a lot longer,” says Robert Vanderbei at Princeton University in New Jersey – though he adds that there is “basically an unlimited number of orbits”, so it may be overkill if anyone sought to find them all.
Perhaps the most important application of the three-body problem is in astronomy, for helping researchers figure out how three stars, a star with a planet that has a moon, or any other set of three celestial objects can maintain a stable orbit.
But these new orbits rely on conditions that are somewhere between unlikely and impossible for a real system to satisfy. In all of them, for example, two of the three bodies have exactly the same mass and they all remain in the same plane.
Knot-like paths
In addition, the researchers did not test the orbits’ stability. It’s possible that the tiniest disturbance in space or rounding error in the equations could rip the objects away from one another.
“These orbits have nothing to do with astronomy, but you’re solving these equations and you’re getting something beautiful,” says Vanderbei.
Aside from giving us a thousand pretty pictures of knot-like orbital paths, the new three-body solutions also mark a starting point for finding even more possible orbits, and eventually figuring out the whole range of winding paths that three objects can follow around one another.
“This is kind of the zeroth step. Then the question becomes, how is the space of all possible positions and velocities filled up by solutions?” says Richard Montgomery at the University of California, Santa Cruz. “These simple orbits are kind of like a skeleton to build the whole system up from.” ”
As suggested by the above article, the field of Celestial Mechanics is still on step zero—the stone age. The found orbits are nothing like heliocentric astronomy and there will be an attempt to use them as a skeleton to "build the whole system up from."
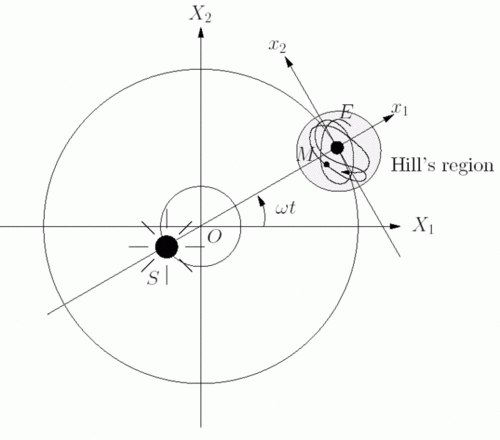
Hill's Region
Astronomer and mathematician George William Hill studied the Three Body Problem. The only way Hill was able to make any progress at all was by using the Restricted Three Body Problem, where one of the bodies was of zero or negligible mass. Even then, the body was still chaotic. The benefit of the Restricted Three Body Problem and the Mass-less moon meant that that the moon would be no longer ejected from the system, as it would usually be. It is confined to what is known as "Hill's Region".
From Scholarpedia's Three Body Problem page by mathematician Alain Chenciner (bio):
http://www.scholarpedia.org/article/Three_body_problem (Archive)
The above depicts a crazy and chaotic moon which even makes a u-turn in mid orbit.
From the text that accompanies the image:
“ The simplest case:
It occurs when, the Jacobi constant being negative and big enough, the zero mass body (we shall still call it the Moon) moves in a component of the Hill region which is a disc around one of the massive bodies (the Earth). This fact already implies Hill's rigorous stability result: for all times such a Moon would not be able to escape from this disc. Nevertheless this does not prevent collisions with the Earth. ”
"Zero mass body" -- One of the bodies in the restricted three body problem is of zero mass.
"Nevertheless this does not prevent collisions with the earth" -- It's still chaotic, even in that simplified version.
One might observe that Newtonian Mechanics most certainly does not naturally default to the heliocentric system of Copernicus.
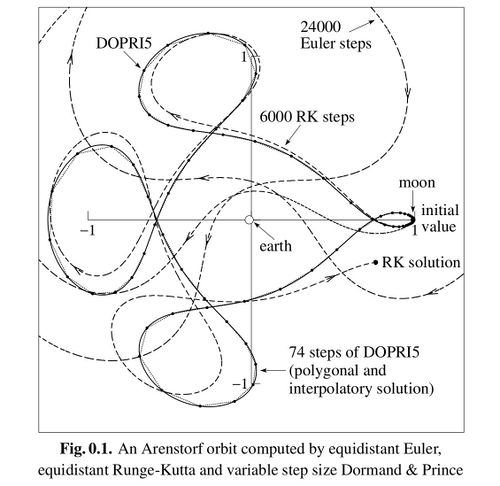
Poliastro
Poliastro, an astrodynamics software developer, shares several numerical methods for the restricted three body problem:
https://twitter.com/poliastro_py/status/993418078036873216?lang=en (Archive)
“ Look at this beautiful plot of several numerical methods for the restricted three body problem taken from Harier et al. "Solving Ordinary Differential Equations I". The use of high order Runge-Kutta methods is pervasive in Celestial Mechanics. Happy Monday! ”
Arenstorf orbits are the knotted closed trajectories which are the result of Restricted Three Body Problem solutions.
Chaos Theory: A Demo
The available solutions to the Two and Three Body Problems are so sensitive that the slightest change or imperfection will tear the entire system apart. From 'Mathematics Applied to Deterministic Problems in Natural Sciences' we read another account of Poincaré's discoveries:
“ As Poincaré experimented, he was relieved to discover that in most of the situations, the possible orbits varied only slightly from the initial 2-body orbit, and were still stable, but what occurred during further experimentation was a shock. Poincaré discovered that even in some of the smallest approximations some orbits behaved in an erratic unstable manner. His calculations showed that even a minute gravitational pull from a third body might cause a planet to wobble and fly out of orbit all together. ”
The orbits are incredibly sensitive. As a very illustrative demonstration, take a look at this online Three Body Problem simulator that uses the symmetrical figure eight pattern, which requires three identical bodies of equal mass which move at very specific momentum and distance in relation to each other.
Demo: Figure-Eight Three Body Problem
Adjust the mass slider values in the upper left of the simulation to something very slight to find what happens. What you will see is a demonstration of Chaos Theory. Any slight modification to a perfect system creates a chain reaction of random chaos.
This is precisely the issue of modeling the Heliocentric System, and why its fundamental system cannot exist. Only very specific, sensitive, and highly symmetrical configurations may exist. The slightest deviation, such as with a system with unequal masses, or the minute influence from a gravitating body external to the system, will cause the entire system to fly apart. The reader is invited to decide for his or her own self whether those scenarios would occur in nature as described by popular theory.
N-Body Solution Galleries
Below are links to galleries of various Three Body and n-Body solutions which have been found. One should note the lack of heliocentric orbits and the inherent semmetry inherent in all orbits.
Wolfram Science
https://www.wolframscience.com/nks/notes-7-4--three-body-problem/ (Archive)
“ In Henri Poincaré's study of the collection of possible trajectories for three-body systems he identified sensitive dependence on initial conditions (see above), noted the general complexity of what could happen (particularly in connection with so-called homoclinic tangles), and developed topology to provide a simpler overall description. With appropriate initial conditions one can get various forms of simple behavior. The pictures below show some of the possible repetitive orbits of an idealized planet moving in the plane of a pair of stars that are in a perfect elliptical orbit. ”
Institute of Physics Belgrade
http://three-body.ipb.ac.rs/ (Archive)
n-Body Choreographies
http://rectangleworld.com/demos/nBody/ (Archive) - Notice that the common theme is highly symmetrical shapes.
Scholarpedia.org
http://www.scholarpedia.org/article/Three_body_problem (Archive)
Euler Math Toolbox
http://euler.rene-grothmann.de/Programs/Examples/Three-Body%20Problem.html (Archive)
Find N-Body Solutions in Your Browser
https://www.i-programmer.info/news/202-number-crunching/8163-find-n-body-solutions-in-your-browser.html - Javascript tool which finds possible N-Body orbits
Supercomputing Challenge
Programming students participated in the New Mexico Supercomputing Challenge to simulate the solar system and found issues with creating basic orbits:
Simulation of Planetary Bodies in the Universe (N-Body) (Archive) (Source Code)
“ Our solar system is an N-body system. N-body simulation is the simulation of astral bodies under gravity, using laws of classical mechanics to define how the astral bodies move. The goal of our project is to model the N-body problem in NetLogo. Code defining how astral bodies interact implements the inverse square law and a gravitational constant to calculate gravitational force between them.
~
Verification and Validation
Even though our model is not entirely accurate, it recreates with graphical simplicity and mathematical correctness of the N-body simulation. Through many many trials, we realize that normal orbits are incredibly complex and hard to obtain through any normal means, and causes us to conclude that our own solar system is an incredible anomaly of the universe. ”
The PDF report explains with additional details that all attempts at observing orbit were unsuccessful.
Universe Sandbox 2
Universe Sandbox 2 (Universe Sandbox ²) is a physics based space simulation developed and published by Giant Army. It has often been claimed that this simulation provides evidence that the Sun-Earth-Moon System and the Solar System are able to be simulated with gravity.
Read the following from a developer blog post and decide whether the program is using a full simulation of gravity:
Working Through the N-Body Problem in Universe Sandbox ² (Archive)
“ By default, the simulations in Universe Sandbox ² try to set an accuracy which prevents orbits from falling apart due to error. This means setting a maximum error tolerance for each step and also making sure the total error doesn’t reach an upper limit.
If you crank up the time step, the simulation then has to take fewer, larger steps. This means the potential for greater error. And the greater the error, the more likely it is that an orbit, which otherwise would be stable, falls apart. Moons crash into planets, Mercury gets thrown out of the solar system — things like that.
This isn’t what most people want in their simulations. But at the same time, most people also don’t want a limit on how fast they can run their simulation. This is a problem.
An imperfect solution
So how can we get around this problem? How can we accurately simulate thousands of objects while still allowing for large steps forward in time? For example, what if you wanted to simulate our solar system on a time scale of millions of years per second so that you could see the evolution of our Sun?
One solution proposed by Thomas, our physics programmer, is to allow for a special mode within simulations running at high time steps. This mode (which of course could be toggled) would collapse the existing n-body simulation into a series of 2-body problems: Moon & Earth, Earth & Sun, Europa & Jupiter, Jupiter & Sun, etc.
Solving a 2-body problem is much easier than solving an n-body problem. Not only is it faster computationally, but there is also a relatively arbitrary difference between figuring out where the two objects will be in one year and where they’ll be in a million years — it still requires just one calculation. So if you collapse an n-body simulation into a series of two-body problems, the simulation could take one big step forward, instead of taking the small steps needed for calculating it as an n-body problem.
The results won’t be entirely accurate, as this method would effectively ignore all gravitational influences outside of the main attractor. As mentioned before, calculating Earth’s orbit by looking at how it interacts with just the Sun is not accurate, as Earth is also affected by every other body. The Sun, however, is the most significant factor by far, because it is much more massive than any other object in our solar system. The other, much smaller forces tend to have little effect overall in non-chaotic systems. So while it’s not correct, it’s close enough when simulating something relatively stable like our solar system.
This isn’t a perfect solution. But we think it could be an improvement over the current system and its limitations, which leave you with the choice of either destabilizing the orbits with massive errors, or waiting days for the simulation to advance the millions of years needed for the Sun to evolve. Neither is particularly interesting. ”
One might ponder that, surely, if all they had to do was to wait days for the simulation to advance millions of years for the 'sun to evolve' in order for heliocentric orbits to become possible, they could simply run that simulation and save its state to use as a baseline for further simulations.
Despite any fanciful allusions that the choice is between either "destabilizing the orbits with massive errors" or "waiting for Sun to evolve," and reassurances that our solar system is stable despite the inability of simulating it—all common statements to excuse away the problems of simulating bodies in heliocentric orbits—its developers freely admit that the program is not using a full simulation of gravity. The article states "By default, the simulations in Universe Sandbox ² try to set an accuracy which prevents orbits from falling apart due to error".
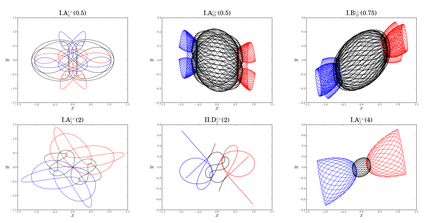
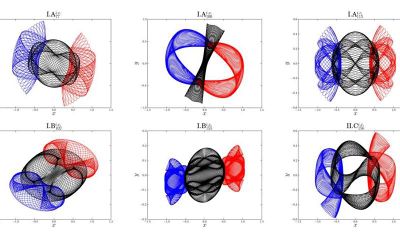
Symmetrical Simulations
The simulations are highly symmetrical with mass restrictions:
Over a Thousand New Solutions - New Scientist
From the New Scientist article Infamous three-body problem has over a thousand new solutions we read:
- “ Perhaps the most important application of the three-body problem is in astronomy, for helping researchers figure out how three stars, a star with a planet that has a moon, or any other set of three celestial objects can maintain a stable orbit.
- But these new orbits rely on conditions that are somewhere between unlikely and impossible for a real system to satisfy. In all of them, for example, two of the three bodies have exactly the same mass and they all remain in the same plane. ”
Clicking on the arxiv.org source at the bottom of the that article takes us to the paper The 1223 new periodic orbits of planar three-body problem with unequal mass and zero angular momentum, where we see at the bottom of p.1:
- “ Therefore, without loss of generality, we consider m1 = m2 = 1 and m3 is varied. ”
We see that these are symmetrical systems:
- FIG. 1. (color online.) Brief overview of the six newly-found families of periodic three-body orbits.
Over 600 New Orbits
Similarly, the phys.org article Scientists discover more than 600 new periodic orbits of the famous three-body problem (Archive) describes the discovery of other symmetrical orbits:
- “ These 695 periodic orbits include the well-known figure-eight family found by Moore in 1993, the 11 families found by Suvakov and Dmitrasinovic in 2013, and more than 600 new families reported for the first time. ”
Quotes
Three Body Dynamics
In Three Body Dynamics and Its Applications to Exoplanets by Professor of Physics Z. Musielak (bio) and astrophysicist Billy Quarles, we see:
“ The three-body problem is one of the best known scientific problems, and there are three main reasons. First, the problem has fundamental importance in science, mathematics and engineering. Second, the problem is truly difficult to solve, which has been manifested by thousands of papers written by numerous outstanding researchers, who have tried (very) hard but failed. Third, the problem can be stated simple enough, so non-experts can understand it and appreciate its importance. As described in this book, all attempts to solve this problem have enriched celestial and classical mechanics, and mathematics with many new methods, powerful theorems, and novel ideas that are already being used in applications in different fields of research. ”
David Gozzard
Physcist David Gozzard (bio) says in his video Weird Orbits - the three body problem (Runtime - 4m):
“ Three hundred and fifty years ago Isaac Newton formulated his theory of gravity Newton's theory unified the heavens and the earth under the same physical laws and neatly explained the orbits of the planets, the motion of comets, and how the moon causes the tides. Although Einstein's general relativity has supplanted Newton's theory as a better model of gravity, Newtonian mechanics got us to the moon and are still used to calculate the trajectories of spacecraft throughout the solar system. In spite of this success and more than three centuries of progress we still do not have a neat set of equations that allow us to calculate the orbital parameters of more than two objects at once. This is called the three-body problem, or more generally the n-body problem. ”
Paul Nahin
From p.132 of Number-Crunching by Dr. Paul J. Nahin (bio):
“ The study of how three massive bodies gravitationally interact is called the three-body problem, and its general solution eluded even the genius of Newton. But, of course, that didn’t mean it was necessarily an impossible problem, just that it was a very, very difficult problem. Perhaps, it was hoped, with advancing technical knowledge and the appearance of an even greater intellect than Newton’s, the three-body problem could be solved. That lure, of being the one that finally did what the great Newton could not, attracted some of the most brilliant analysts over the next 250 years. Such luminaries as the Swiss Leonhard Euler (1707-1783), the French Joseph Lagrange (1736-1813), and the German Carl Jacobi (1804-1851), for example, all tried their hands at it, but except for limited partial successes made under special, restrictive assumptions, the general solution of the three-body problem defeated every one of them. ”
Vinay Ambegaokar
In the Chaos chapter (Archive) of Reasoning about Luck: Probability and Its Uses in Physics, its author physics professor Vinay Ambegaokar (bio) tells us that the three-body problem is not studied in the physics curriculum:
“ The next simplest case is the ‘three body problem’ - sun, earth, and moon, for example - taking into account the attraction between each body and the other two. No simple solution to this problem exists, and it is not studied in the physics curriculum. ”
Isaac Newton
On p.174 of Medical Reasoning: The Nature and Use of Medical Knowledge (Archive) its author Erwin B. Montgomery shares this quote from Newton:
“ An example of a system that can be described explicitly by a mathematical metaphor proved unsolvable (at least explicitly in algebraic or integral functions) is the three-body problem, such as the orbits of the earth, moon, and sun when all three are considered simultaneously. While the two-body problem is solvable, such as the orbits of the earth and moon, even Newton recognized the difficulty and indeed potential intractability of the three-body problem, commenting in 1684 that “to define these motions by exact laws admitting of easy calculation exceeds, if I am not mistaken, the force of any human mind” (from a draft of De Motu, tentatively dated in December 1684; Wilson 1989). ”
Martin Gutzwiller
The end section of a paper titled Moon-Earth-Sun: The oldest three-body problem (Archive) by physicist Martin C. Gutzwiller (bio) concludes that Newton's laws are not a sufficient explanation:
“ The three-body problem teaches us a sobering lesson about our ability to comprehend the outside world in terms of a few basic mathematical relations. Many physicists, maybe early in their careers, had hopes of coordinating their field of interest, if not all of physics, into some overall rational scheme. The more complicated situations could then be reduced to some simpler models in which all phenomena would find their explanation. This ideal goal of the scientific enterprise has been promoted by many distinguished scientists [see Weinberg’s (1992) Dream of a Final Theory, with a chapter ‘‘Two Cheers for Reductionism’’]....Many physicists may be tempted to see in Newton’s equations of motion and his universal gravitation a sufficient explanation for the three-body problem, with the details to be worked out by the technicians. But even a close look at the differential equations (29) and (30) does not prepare us for the idiosyncracies of the lunar motion, nor does it help us to understand the orbits of asteroids in the combined gravitational field of the Sun and Jupiter. ”
Mark Cunningham
On p.189 of Neoclassical Physics by physicist Mark Cunningham (bio) we read the following (Archive):
Classical Mechanics
“ Issac Newton's notable success in providing a theoretical explanation for the motion of planets around the sun was followed quickly by his realization that the gravitational problem involving three bodies was immensely more difficult than the two-body problem. Where the two-body problem, as we have seen in Chapter 2, can be solved exactly, Newton's attempts to provide a concise mathematical description of the earth-sun-moon system were not successful.1 This, of course, is not due to Newton's lack of mathematical skills. Indeed, a series of notable mathematicians all applied their skills to the problem but without success, although it depends somewhat on how one defines success. It is true that no general solutions of the three-body problem have been constructed but the assault on the problem led to powerful new mathematical methods for understanding dynamical systems.2 ”
Yet again, we find direct statements telling us that the venture of describing or simulating the earth-sun-moon system has been unsuccessful, from the time of Newton up to present. Numerous and notable mathematicians over the years have attempted to describe or simulate the earth-sun-moon system without success—telling us everything that we need to know about the systems of Newton and Copernicus.
Richard D. Mattuck
Contrary to common dogma, the ability of various fields to describe physical systems based on the underlying laws has been going down with time, not up. Richard D. Mattuck writes in his A Guide to Feynman Diagrams in the Many-Body Problem (Archive):
The Many-Body Problem for Everybody
“ How many bodies are required before we have a problem? G. E. Brown [bio] points out that this can be answered by a look at history. In eighteenth-century Newtonian mechanics, the three-body problem was insoluble. With the birth of relativity around 1910 and quantum electrodynamics in 1930, the two- and one-body problems became insoluble. And within modern quantum field theory, the problem of zero bodies (vacuum) is insoluble. So, if we are out after exact solutions, no bodies at all is already too many! ”
Stability of the Solar System
It has been asserted that Laplace and Lagrange demonstrated the stability of the Solar System. On this topic, Professor H. Scott Dumass tells us in The KAM Story (Archive):
“ In the early 19th century, building on earlier work of Lagrange, 12 Laplace ‘proved’ the stability of the solar system, and although this work was an important step and is mathematically correct as far as it goes, it was soon recognized that he had not shown stability for the n body problem, but rather for an attenuated version of it in which higher-order interactions between planets are ignored. Such claims and half-successes by the mathematical giants of the ages (and many other less-than-giants) of course only added celebrity to the n body problem, and to the stability problem in particular. ”
Later researchers went on to 'simulate' the solar system with two body approximation and geometry preserving schemes. See the pages Numerical Solutions and Symplectic Integrators.
N-Body Symmetry
Code documentation for N-Body simulation software at Rosetta Code states the following:
https://rosettacode.org/wiki/N-body_problem (Archive)
“ The slightest perturbation from symmetry causes the system to become unstable. ”
See Also
- Three Body Problem - The heliocentric Sun-Earth-Moon system cannot be simulated
- Numerical Solutions - The available solutions for celestial systems do not fully simulate gravity
- Perturbation Methods - Epicycles are still used for astronomical prediction
- Eclipse Prediction - The eclipses are predicted with cycles and patterns
- Symplectic Integrators - A special method of orbital simulation which preserves geometry and forces stability