Three Body Problem
The Three Body Problem is a four hundred year old problem of mathematics which has its roots in the attempts to simulate a heliocentric Sun-Earth-Moon system.
“ Describing the motion of any planetary system (including purely imaginary ones that exist only on paper) is the subject of a branch of mathematics called celestial mechanics. Its problems are extremely difficult and have eluded the greatest mathematicians in history. ” — Paul Trow, Chaos and the Solar System (Archive)
400 Years of Defiance
In The Physics Problem that Isaac Newton Couldn't Solve (Archive) cosmologist Robert Scherrer informs us:
“ There's a physics problem so difficult, so intractable, that even Isaac Newton, undoubtedly the greatest physicist who ever lived, couldn't solve it. And it's defied everyone else's attempts ever since then.
This is the famous three-body problem. When Newton invented his theory of gravity, he immediately set to work applying it to the motions of the planets in the solar system. If you have a planet orbiting a much larger body, like the sun, and the orbit is circular, then the problem is easy to solve -- it's something that's done in a high school physics class.
But a circular orbit isn't the most general possibility, and sometimes one body isn't much smaller than the object it orbits (think of the Moon going around the Earth). This more complicated case can still be solved -- Newton showed that the two bodies orbit their common center of mass in elliptical orbits. In fact, this prediction of elliptical orbits really cemented the case for Newton's theory of gravity. The calculation is a lot trickier than for circular orbits, but we still throw it at undergraduate physics majors in their second or third year.
Now add a third body, and everything falls apart. The problem goes from one that a smart undergraduate can tackle to one that has defied solution for 400 years. ”
Newton's Solution
Mathematician and astronomer Issac Newton is credited to have "brought the laws of physics to the solar system."1 In regards to the multi-body problems of his system, Newton famously invoked divine intervention as his solution:
“ At the beginning of the 18th century, Newton famously wrote that the solar system needed occasional divine intervention (presumably a nudge here and there from the hand of God) in order to remain stable.11 This was interpreted to mean that Newton believed his mathematical model of the solar system—the n body problem—did not have stable solutions. Thus was the gauntlet laid down, and a proof of the stability of the n body problem became one of the great mathematical challenges of the age.
11Newton's remarks about divine intervention appear in Query 23 of the 1706 (Latin) edition of Opticks, which became Query 31 of the 1717 (2nd Edition) edition see Quote Q[New] in Appendix E). Similar 'theological' remarks are found in scholia of the 2nd and 3rd editions of Principia, and in at least one of Newton's letters. In a 1715 letter to Caroline, Princess of Wales, Leibniz observed sarcastically that Newton had not only cast the Creator as a clock-maker, and a faulty one, but now as a clock-repairman (see [Klo73], Part XXXIV, pp. 54-55). ”
1The University of California San Diego credits Newton as providing the laws of physics for the Solar System (Archive):
“ Then came Isaac Newton (1642-1727) who brought the laws of physics to the solar system. Isaac Newton explained why the planets move the way they do, by applying his laws of motion, and the force of gravitation between any two bodies, letting the force decrease with the square of the distance between the two bodies. ”
Henri Poincaré
http://n.ethz.ch/~stiegerc/HS09/Mechanik/Unterlagen/Lecture13.pdf (Archive)
“ 9.2.1 History
In 1885, Poincaré entered a contest formulated by the King Oscar II of Sweden in honor of his 60th birthday. One of the questions was to show the solar system, as modeled by Newton’s equations, is dynamically stable. The question was nothing more than a generalization of the famous three body problem, which was considered one of the most difficult problems in mathematical physics. In essence, the three body problem consists of nine simultaneous differential equations. The difficulty was in showing that a solution in terms of invariants converges (This isn’t likely to happen today - that the birthday of any contemporary world leader is celebrated by a mathematical competition!). Henri Poincare was a favorite to win the prize, and he submitted an essay that demonstrated the stability of planetary motions in the three-body problem (actually the restricted problem, in which one test body moves in the gravitational field generated by two others). In other words, without knowing the exact solutions, we could at least be confident that the orbits wouldn't go crazy; more technically, solutions starting with very similar initial conditions would give very similar orbits. Poincaré's work was hailed as brilliant and he was awarded the prize.
But as his essay was being prepared for publication in Acta Mathematica, a couple of tiny problems were pointed out by Edvard Phragmn, a Swedish mathematician who was an assistant editor at the journal. Gsta Mittag-Leffler, chief editor, forwarded Phragmn's questions to Poincaré, asking him to fix up these nagging issues before the prize essay appeared in print. Poincaré went to work, but discovered to his consternation that one of the tiny problems was in fact a profoundly devastating possibility that he hadn't really taken seriously. What he ended up proving was the opposite of his original claim. Three-body orbits were not stable at all. Not only were the orbits none periodic, they didn't even approach some sort of asymptotic fixed points. Now that we have computers to run simulations, this kind of behavior is less surprising, but at the time it came as an utter shock. In his attempt to prove the stability of planetary orbits, Poincaré ended up inventing chaos theory. ”
Ask A Mathematician
https://www.askamathematician.com/2011/10/q-what-is-the-three-body-problem/
“ Q: What is the three body problem?
The three body problem is to exactly solve for the motions of three (or more) bodies interacting through an inverse square force (which includes gravitational and electrical attraction).
The problem with the 3-body problem is that it can’t be done, except in a very small set of frankly goofy scenarios (like identical planets following identical orbits). ”
A Thousand New Solutions
From a New Scientist article titled Infamous three-body problem has over a thousand new solutions:
“ The new solutions were found when researchers at Shanghai Jiaotong University in China tested 16 million different orbits using a supercomputer.
...
Perhaps the most important application of the three-body problem is in astronomy, for helping researchers figure out how three stars, a star with a planet that has a moon, or any other set of three celestial objects can maintain a stable orbit.
But these new orbits rely on conditions that are somewhere between unlikely and impossible for a real system to satisfy. In all of them, for example, two of the three bodies have exactly the same mass and they all remain in the same plane.
Knot-like paths
In addition, the researchers did not test the orbits’ stability. It’s possible that the tiniest disturbance in space or rounding error in the equations could rip the objects away from one another.
“These orbits have nothing to do with astronomy, but you’re solving these equations and you’re getting something beautiful,” says Vanderbei.
...
Aside from giving us a thousand pretty pictures of knot-like orbital paths, the new three-body solutions also mark a starting point for finding even more possible orbits, and eventually figuring out the whole range of winding paths that three objects can follow around one another.
...
“This is kind of the zeroth step. Then the question becomes, how is the space of all possible positions and velocities filled up by solutions?” says Richard Montgomery at the University of California, Santa Cruz. “These simple orbits are kind of like a skeleton to build the whole system up from.” ”
Two Bodies of Equal Mass
The research group with the super computer published another study titled: Over a thousand new periodic orbits of a planar three-body system with unequal masses
“ Abstract
The three-body problem is common in astronomy, examples of which are the solar system, exoplanets, and stellar systems. Due to its chaotic characteristic, discovered by Poincare, only three families of periodic three-body orbits were found in 300 years, until 2013 when Suvakov and Dmitra ˇ sinovi ˇ c ( ´ 2013, Phys. Rev. Lett., 110, 114301) found 13 new periodic orbits of a Newtonian planar three-body problem with equal mass. Recently, more than 600 new families of periodic orbits of triple systems with equal mass were found by Li and Liao (2017, Sci. China-Phys. Mech. Astron., 60, 129511). Here, we report 1349 new families of planar periodic orbits of the triple system where two bodies have the same mass and the other has a different mass. None of the families have ever been reported, except the famous “figure-eight” family. In particular, 1223 among these 1349 families are entirely new, i.e., with newly found “free group elements” that have been never reported, even for three-body systems with equal mass. It has been traditionally believed that triple systems are often unstable if they are non- hierarchical. However, all of our new periodic orbits are in non-hierarchical configurations, but many of them are either linearly or marginally stable. This might inspire the long-term astronomical observation of stable non-hierarchical triple systems in practice. In addition, using these new periodic orbits as initial guesses, new periodic orbits of triple systems with three unequal masses can be found by means of the continuation method, which is more general and thus should have practical meaning from an astronomical viewpoint. ”
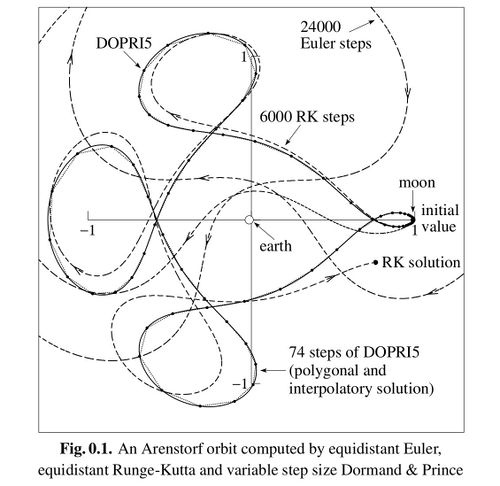
Poliastro
Poliastro, an astrodynamics software developer, shares several numerical methods for the restricted three body problem:
https://twitter.com/poliastro_py/status/993418078036873216?lang=en
“ Look at this beautiful plot of several numerical methods for the restricted three body problem taken from Harier et al. "Solving Ordinary Differential Equations I". The use of high order Runge-Kutta methods is pervasive in Celestial Mechanics. Happy Monday! ”
Arenstorf orbits are the knotted closed trajectories which are the result of Restricted Three Body Problem solutions.
Chaos Theory: A Demo
The available solutions to the Three Body Problem, beyond being unlike anything seen in Heliocentric Theory, are so sensitive that the slightest change or imperfection will tear the entire system apart. As a very illustrative demonstration, take a look at this online Three Body Problem simulator that uses the simplest possible figure eight pattern, which requires three identical bodies of equal mass that move at very specific momentum and distance in relation to each other.
Demo: Figure-Eight Three Body Problem
Adjust the slider values in the upper left to something very slight to find what happens. What you will see is a demonstration of Chaos Theory. Any slight modification to the system creates a chain reaction of random chaos.
This is precisely the issue of modeling the Heliocentric System, and why its fundamental system cannot exist. Only very specific and very sensitive configurations may exist. The slightest deviation, such as with a system with unequal masses, or the minute influence from a gravitating body external to the system, will cause the entire system to fly apart. The reader is invited to decide for his or her own self whether those scenarios would occur in nature as described by popular theory.
Highly Sensitive Orbits
From 'Mathematics Applied to Deterministic Problems in Natural Sciences' we read another account of Poincaré's discoveries:
“ As Poincaré experimented, he was relieved to discover that in most of the situations, the possible orbits varied only slightly from the initial 2-body orbit, and were still stable, but what occurred during further experimentation was a shock. Poincaré discovered that even in some of the smallest approximations some orbits behaved in an erratic unstable manner. His calculations showed that even a minute gravitational pull from a third body might cause a planet to wobble and fly out of orbit all together. ”
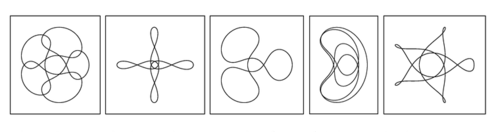
N-Body Solution Galleries
Wolfram Science
https://www.wolframscience.com/nks/notes-7-4--three-body-problem/
“ In Henri Poincaré's study of the collection of possible trajectories for three-body systems he identified sensitive dependence on initial conditions (see above), noted the general complexity of what could happen (particularly in connection with so-called homoclinic tangles), and developed topology to provide a simpler overall description. With appropriate initial conditions one can get various forms of simple behavior. The pictures below show some of the possible repetitive orbits of an idealized planet moving in the plane of a pair of stars that are in a perfect elliptical orbit. ”
Institute of Physics Belgrade
n-Body Choreographies
http://rectangleworld.com/demos/nBody/
Scholarpedia.org
http://www.scholarpedia.org/article/Three_body_problem
Euler Math Toolbox
http://euler.rene-grothmann.de/Programs/Examples/Three-Body%20Problem.html