Difference between revisions of "Moon Tilt Illusion Supplement"
Tom Bishop (talk | contribs) |
Tom Bishop (talk | contribs) |
||
| Line 44: | Line 44: | ||
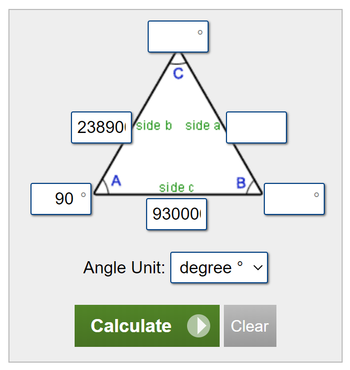
[[File:Triangle Calc.png|350px]] | [[File:Triangle Calc.png|350px]] | ||
| − | We put in the distances in miles to the RE Moon at | + | We put in the distances in miles to the RE Moon at Side b, the distance to the RE Sun at Side c, and 90 degrees at the observer at Angle A. This produces the following: |
https://www.calculator.net/triangle-calculator.html?vc=&vx=238900&vy=&va=90&vz=93000000&vb=&angleunits=d&x=70&y=8 | https://www.calculator.net/triangle-calculator.html?vc=&vx=238900&vy=&va=90&vz=93000000&vb=&angleunits=d&x=70&y=8 | ||
[[File:Triangle_Calc_Result.png|800px]] | [[File:Triangle_Calc_Result.png|800px]] | ||
Revision as of 17:29, 27 June 2020
The Moon Tilt Illusion Supplement page addresses supplementary arguments related to the Moon Tilt Illusion.
Higher Sun Argument
According to the Round Earth Thoery's Perspective Explanation the illuminated portion of the Moon is tilted upwards by perspective. If this is true then it should not be possible to view the Sun and Moon misaligned at the same time, in the same field. However, it has been reported that both the Moon and Sun have been seen simultaneously, misaligned to each other.
As response it is claimed that since the sun's light is parallel and hitting the Earth-Moon system as a whole from the side, the Moon will see a higher Sun than the Earth. The Sun will appear from a different position in space to the Moon, causing the Moon's illuminated area to point to a position above the Sun that we see from Earth.
In contrast to this argument, the angles are not perfectly parallel under the Round Earth system. When assessing the parallax displacement between an observer on Earth and an observer on the Moon the Sun will be in essentially the same point in space.
Angular Diameter Example
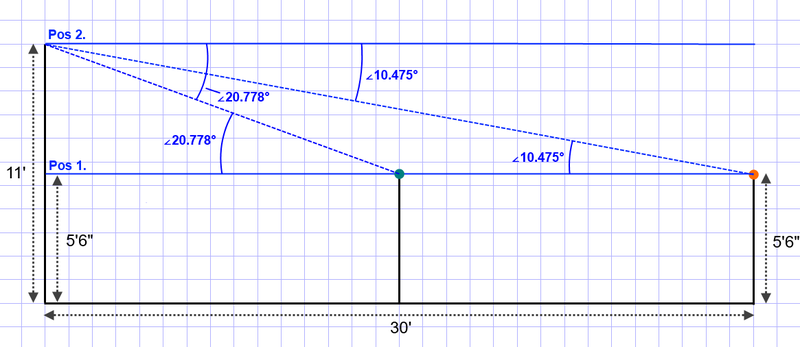
As an example, if your eye is at an altitude of 5 feet, 6 inches, and there is an object, say a Green Ball on a post 15 feet away from you at the same altitude, and an Orange Ball on a post 30 feet away from you, which is also at altitude of 5 feet, 6 inches, then the position of both the green and orange balls will be parallel on the horizontal. The path to that object will be at your eye level.
Instead, lets say that you step on a boulder that is 5 foot, 6 inches in height. The new altitude of your eye is 11 feet in height. We know that the green and orange balls are on posts which are 5 ft 6 in below that 11 foot elevation where it would need to be to be parallel to the eye.
In order to find the position of the green and orange balls in degrees below eye level, we can use an angular diameter calculator to calculate the missing space above the green and orange ball, to determine how far below eye level those balls will be to the observer.
For the Green Ball, 5.5 feet at 15 feet produces an angular diameter of 20.778 degrees. For the Orange Ball, 5.5 feet at 30 feet produces an angular diameter of 10.475 degrees.
Diagram
We see that as a body moves further from you, it gets closes to your eye level, and displaces fewer degrees in space between two altitudes.
Adopting the above to the Earth and Moon in the RE system, we had from the previous diagram an observer seeing the Sun parallel on the horizontal at eye level, midway setting into the horizon. The Moon was directly over the observer. In order to calculate the displacement of the Sun in the sky between to an observer the Moon we may use the angular diameter calculator with the distances involved.
Input
g: 238900
r: 93000000
Output
a: 0.147 degrees
Hence, if the observer was able to move from the Earth to the Moon the Sun would be seen from essentially the same position in space. The diagram of the Sun appearing in two different places is misleading, as it does not show the entire scene and the angles are not exactly parallel to the Sun.
Triangle Calculator
Next, we look at a triangle calculator, which will compute the missing values:
We put in the distances in miles to the RE Moon at Side b, the distance to the RE Sun at Side c, and 90 degrees at the observer at Angle A. This produces the following: