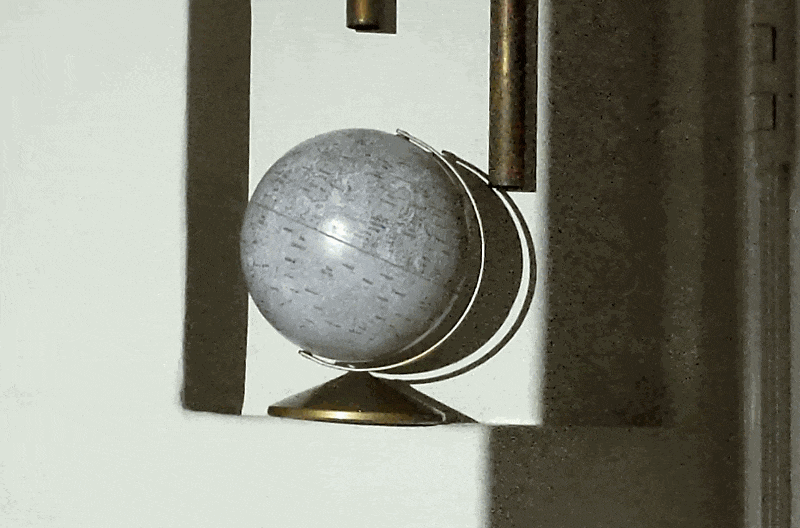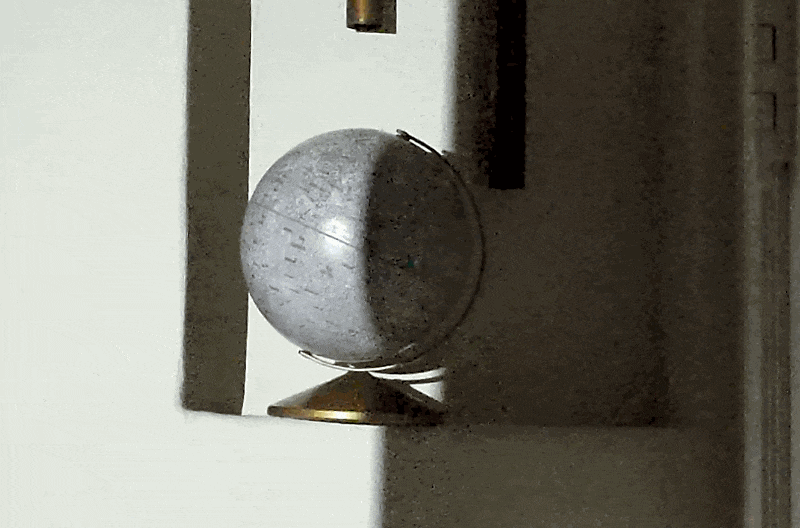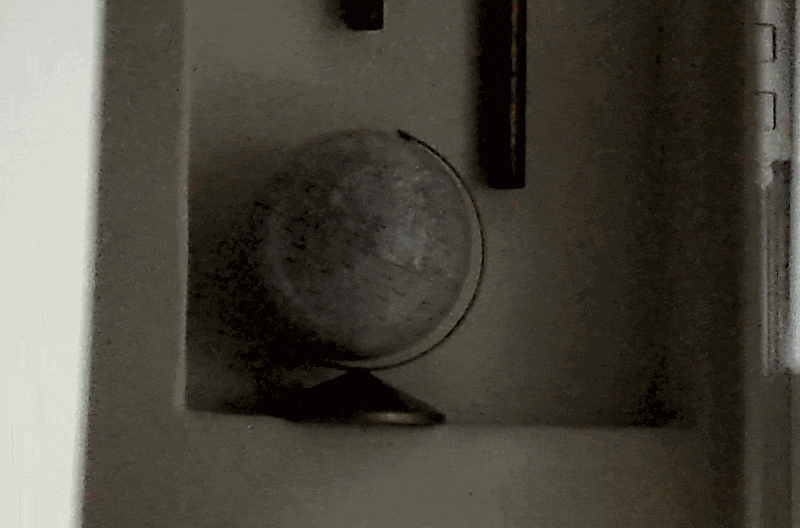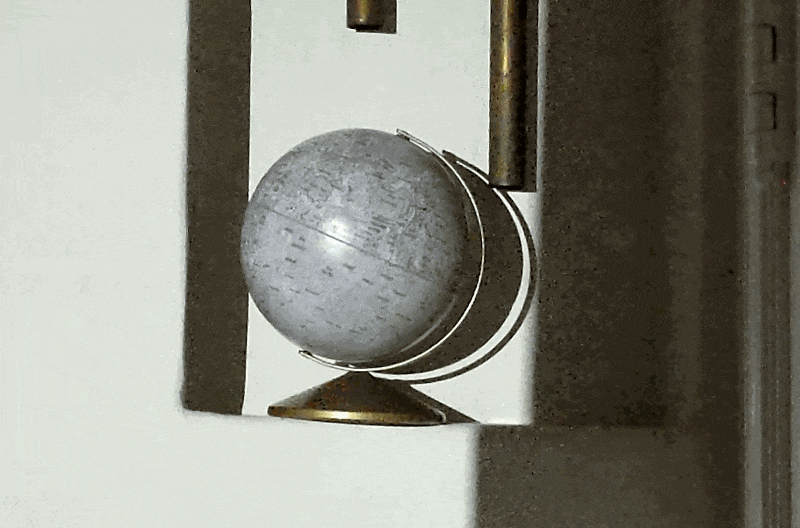Lunar Eclipse due to Electromagnetic Acceleration
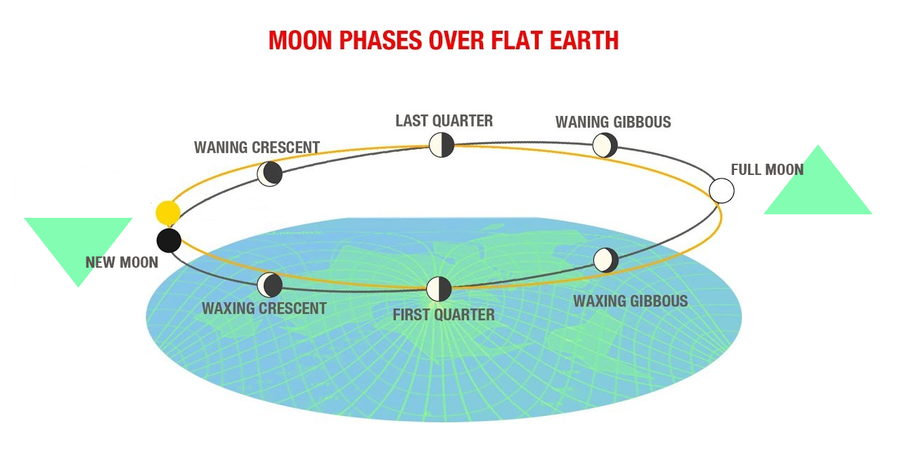
According to the Flat Earth Theory's celestial model of Electromagnetic Acceleration the Sun illuminates the Moon through the mechanism of its upwardly curving rays. At various points near the Sun, the Moon will be lit at various angles, causing the range of phases. When the Moon is close to the Sun the New Moon occurs, and when it is far from the Sun the rays are vertical at the Moon's position, causing the Full Moon. The Lunar Eclipse happens about 2 to 5 times a year on an occasion where the path of the Full Moon wanders too far from the Sun, temporarily exiting the sunlight boundary. A lack of light causes darkness to manifest upon the lunar surface.
Lunar Phase Overview
The EA explanation of the occurrence of the Lunar Eclipse is related to the Lunar Phases. From the Electromagnetic Acceleration - Lunar Phases section we see:
“ When one observes the phases of the Moon they are seeing the Moon's day and night, a shadow created from the Sun illuminating half of the spherical Moon at any one time. ...The curved rays of the Sun results in the phases upon the Moon's surface. The plane of the Moon's route is at an inclination to the plane of the Sun's ecliptic, with its highest side opposite from the Sun. When the Moon is far from the Sun and higher than it, the Full Moon occurs. When the Moon is closer to the Sun and lower than it, the New Moon occurs1. The Moon moves at a slightly slower rate than the Sun's motion across the sky, lagging about 50 minutes behind daily, causing the range of phases. The time between two Full Moons, or between successive occurrences of the same phase, is about 29.53 days (29 days, 12 hours, 44 minutes) on average. ”
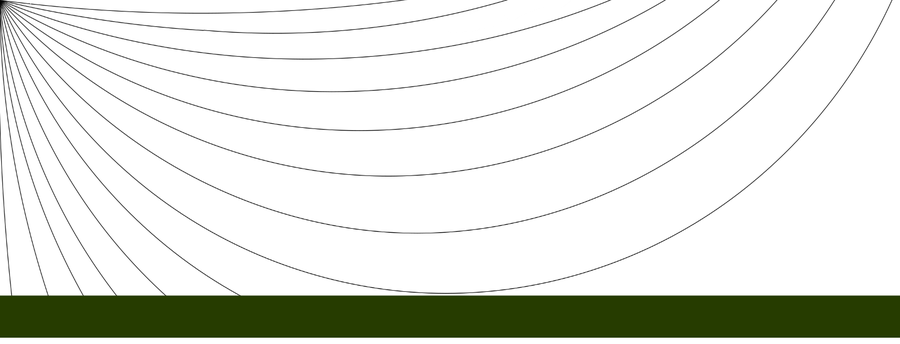
Sample large-scale Sun ray diagram (side view):
Cause of Lunar Eclipse
As seen in the above, both the Moon and Sun follow similar paths near the ecliptic. On large scales light is curving upwards, as per Flat Earth's celestial model of Electromagnetic Acceleration. The Earth's presence limits the extent of the outward parabolic rays. The Lunar Eclipse occurs on an occasion when the Moon is on the opposite side of the ecliptic from the Sun and its diurnal circular path temporarily wanders "out of bounds," beyond the vertical rays of the Sun.
The scheme described above will follow a typical geometrical pattern. It can be predicted that the Lunar Eclipse will occur when:
- - The Moon is Full
- - The Moon is on opposite extremes of the Earth from the Sun
- - The Moon and Sun are near their greatest latitudinal displacement from each other
Another consequence will be that the Lunar Eclipse will turn red, since the outer-most rays of the Sun create parabolic arcs which dip down and pass through the atmosphere of the Earth. When the Sun's light is horizontal against the atmosphere the light will become red due to Rayleigh scattering, as seen when the sky turns red during sunsets. It is also apparent that, since the Sun and Moon are on opposite extremes of the ecliptic during the Lunar Eclipse, the path which intersects the atmosphere will be through an area near the Pole. If this geometry is true, it follows that conditions in the North may affect the appearance of the Lunar Eclipse. And indeed, astronomers have noted that during periods of high auroral activity the Lunar Eclipse has been seen to be very bright.[1]
Curved Shadow
One of Aristotle's proofs for the rotundity of the world was the shape of the shadow on the Moon during a Lunar Eclipse. Aristotle reasoned that only a round earth could cause a round shadow. Since the shadow is round on the Moon, the Earth must also be round. Although a seemingly reasonable statement at a glance, this is not necessarily the case. Since the surface of the Moon is that of a convexly curved sphere, a straight or slightly concave shadow can display as convexly curved upon the Moon.
In a dark room place a flashlight onto a ledge, shining at a sphere about eleven or so feet away. Use a folder to block the path of light, observing how the shadow behaves on the sphere.
We see that a shadow on a sphere can curve on its own, due to the convexity of the sphere. Under EA explanation for the Lunar Eclipse the shadow at the boundary is only very slightly concave at the Moon's location, essentially flat, as compared to the highly convex surface of the Moon.
Lunar Eclipse Comparison
Compare the warping of the shadow in the above example to the shadow on the real Moon during a Lunar Eclipse:
Not Straight Across
Interestingly, during the eclipse the shadow seen does not travel straight across the Moon's face, but appears to turn mid-stride, making a 110 - 120 degree angle across its surface.
EA model - overhead:
Lunar Eclipse Timelapses
In the below examples of the Lunar Eclipse notice that the shadow does not go straight across the Moon's face, but seems to make a turn mid-way through.
Lunar Eclipse - March 2007
Lunar Eclipse - October 2004 - California
October 2004 Lunar Eclipse taken from Hayward, California
Lunar Eclipse - September 2015 - Europe
https://lrtimelapse.com/news/lunar-eclipse-2015-timelapse/ (Archive)
Lunar Eclipse - January 2018 - Griffith Observatory
Runtime: 1m
Additional:
- Video: Lunar Eclipse - December 2010 - Florida (Runtime: 2m)
Deliberate Rotation of Lunar Face
An assessment of Lunar Eclipse montages available online shows that a small number of examples display eclipse shadows which do appear to move straight across the Moon's visible disk. However, a closer inspection of these examples reveal that the lunar face sequences have been rotated in Photoshop or post-processing for what appears to be artistic reasons, likely to give the expected appearance of the shadow moving straight across.
Example: https://www.sapeople.com/2018/07/28/more-photos-of-last-nights-moon-a-total-lunar-eclipse-of-the-heart/ (Archive)
Compare the features of the Moon's face in above montage to the timelapses and videos in the previous section.
Bright Lunar Eclipses
Under the EA explanation for the Lunar Eclipse it is seen that when the Sun and Moon are on opposite sides from each other the dipping rays must pass through the auroral zone on their way to the Moon. On occasion the Lunar Eclipse will be seen to be significantly brighter. It has been historically remarked by European astronomers that there is an association with the presence of auroral activity and bright occurrences of the Lunar Eclipse.
See the following remarks:
Royal Astronomical Society
Monthly Notices of the Royal Astronomical Society, Nov 1845 - Jun 1847
Remarkable Appearances during the total Eclipse of the Moon on March 19. 1848. (Archive)
Extract of a Letter from Mr. Forster, Bruges.
“ I wish to call your attention to the fact which I have clearly ascertained, that during the whole of the late lunar eclipse of March 19, the shaded surface presented a luminosity quite unusual, probably about three times the intensity of the mean illumination of an eclipsed lunar disc. The light was of a deep red colour. During the totality of the eclipse, the light and dark places on the face of the moon could be almost as well made out as in an ordinary, dull moonlight night, and the deep red colour, when the sky was clearest, was very remarkable from the contrasted whiteness of the stars. My observations were made with different telescopes, but all presented the same appearance, and the remarkable luminosity struck every one. The British consul of Ghent, who did not know that there was an eclipse, wrote to me for an explanation of the blood-red colour of the moon at 9 o'clock.
The sky was of unusual brilliancy, as often occurs between showers; there was a bright aurora in the north, and a most magnificent meteor descended obliquely towards the north-west horizon about the time of the central eclipse. The western margin of the disc resented a rough, uneven appearance at this time. What would be the effect on the dark surface of the moon of extensive aurora borealis on our earth ?"
Mr. Walkey, who observed the eclipse at Clyst-St. Lawrence, near Collumpton, says the appearances were as usual till 20 minutes to 9. “ At that period, and for the space of the next hour, instead of an eclipse, or the umbra of the earth being the cause of the total obscurity of the moon, the whole phase of that body became very quickly and most beautifully illuminated, and assumed the appearance of the glowing heat of fire from the furnace, rather tinged with a deep red. The above description I gave to the editor of one of the Exeter papers, and some one has attempted to solve the peculiarity of the appearance by speaking of the umbra and penumbra, which might have been the cause of it. But such a solution has nothing to do with the appearance, the whole disk of the moon being as perfect with light as if there had been no eclipse whatever.
Having spoken of this appearance, I was informed by one or two individuals that they had seen, between twenty minutes to nine and twenty minutes to ten, a very luminous appearance of the aurora borealis. Now, it strikes me that the light reflected from this northern effulgence might have caused the luminous appearance of the moon in this part of the country at the time when it was under the perfect umbra of the earth in other portions of England.
Many more than three-score years have passed with myself, and during that period I have several times beheld an eclipse of the moon, but never before did my eyes behold the moon positively giving good light from its disk during a total eclipse. The phases of the moon perfectly corresponded with the authorised diagram up to the period of 8h 40m and after 9h 40m to the end of the eclipse. ”
Nature
Nature, Volume 16, p.287
OUR ASTRONOMICAL COLUMN (Archive)
“ Though we are accustomed to speak of a total eclipse of the moon, as is well known, it rarely happens that she disappears while in the earth’s shadow. The physical features of interest to which allusion is made above consist chiefly in the variations of the coppery and other tints which spread over her surface, and in the great majority of eclipses render her more or less conspicuously visible, during her passage through the shadow; and as these variable features depend upon the state of the atmosphere at the time round the edge of the earth’s disc as seen from the moon, with respect to transparency or more or less prevalence of cloud therein—the aspect which a particular eclipse is likely to present does not admit of prediction. In the eclipse of June 15, 1620, Kepler states that the moon wholly disappeared, while stars of the fifth magnitude were visible in the neighbourhood, and He velius failed to see her even with a telescope during the eclipse of April 14, 1642 (not April 25, as stated in many astronomical treatises). But perhaps one of the most striking instances of the kind is afforded by the eclipse of May 18, 1761, observed by the Swedish astronomer Wargentin at Stockholm ; eleven minutes after the total immersion he could not perceive the slightest trace of the moon either with the naked eye or with the telescope, yet the night was very clear and the stars shining in her vicinity; but about forty minutes later, with a two-foot telescope, he discovered our satellite by a faint light on the border of the disc.
As an instance of the contrary nature, where the moon has been so strongly illuminated during her presence in the shadow, as to admit of the various markings upon her surface being seen with distinctness, and even to lead persons to doubt her being eclipsed, mention may be made of the eclipse on the morning of December 23, 1703, which was observed by various astronomers in the south of France. At Avignon, during the whole duration of the passage through the earth’s shadow, “the moon appeared extraordinarily illuminated, and of a very bright red, so that it might have been supposed that she was transparent, and that the sun was behind her globe, and that his rays passed through in the same manner that they are seen to traverse certain stones, which are slightly diaphanous.” It is singular, however, that while this was the aspect of the phenomenon at Avignon, different features should have been noted at Montpellier, particularly the total disappearance of the moon, rather quickly towards 6h. 30m. A.M., though the night was as transparent as could have been wished ; it is mentioned that the twilight was already very sensible, but that the invisibility of the moon could not be wholly attributed to this cause, since many stars were shining in the same quarter of the sky. A later instance of the same kind occurred on March 19, 1848, recorded by observers in England, Ireland, and Belgium, when the moon’s disc was intensely bright, coppery red. The uninitiated were doubtful of there being any eclipse. It is worthy of mention that conspicuous aurora borealis was present during the night. ”
The Observatory
The Observatory, A Montly Review of Astronomy - Vol. XXVI, 1903
Bright Lunar Eclipses (Archive)
“ GENTLEMEN,— Observations of the eclipse of the Moon on October 6 next will be looked for with interest, as the darkened features of the lunar surface on October 4, 1884, were repeated in the next eclipse as viewed from Tasmania. A similar state of things may be expected on the coming occasion.
As the presence of volcanic dust in the atmosphere seems the explanation of black eclipses of the Moon, enquiry naturally arises as to what is the cause of unusually bright ones. The best authenticated instances of this are in April 1623, December 1703, and 19 March, 1848.
As to that of 1848, the most commonly quoted account is that given by Mr. Foster, of Bruges, to whom the British Consul at Ghent wrote for an explanation of the peculiar colour of the Moon. But it must be noted that Mr. Foster adds “ there was a bright aurora in the north.” The best account seems to be given by Mr. Walkey, who observed at Clyst-S. Laurence (Devon). A portion of his description in the ‘ Monthly Notices R. Ast. Soc.’ may as well be quoted. He says that at 8.40 “and for the space of the next hour, instead of an eclipse or the umbra of the Earth being the cause of the total obscurity of the Moon, the whole of that body became very quickly and most beautifully illuminated, and assumed the appearance of glowing heat of fire from the furnace, rather tinged with a deep red....the whole disc of the Moon being as perfect with light as if there had been no eclipse whatever....I was informed by one or two individuals that they had seen between 8.40 and 9.40 a very luminous appearance of the aurora borealis....Many more than threescore years have passed with myself, and during that period I have several times beheld an eclipse of the Moon, but never before did my eyes behold the Moon positively giving good light from its disc during a total eclipse.” A letter from Rev. C. Mayne (Killaloe), in ‘Monthly Notices’ for May, says: “ I am told that aurora was visible the same night.”
As to the total eclipse of 1703, while the usually quoted description of the eclipse as seen from Avignon implies unusual brightness, different conditions prevailed at Montpellier. It cannot be affirmed that there was no aurora, as in a ‘General Chronological History of Air, Seasons, Meteors, &c.,’ London, 1749, under the head of the year 1717 we have the following remark :—“This spring the Aurora which had now continued 17 or 18 years came to its height ”; and this includes 1703.
The eclipse of 1623, April 15, was one of 10 3/4 digits (not total). It was observed by Gassendi. G. Wendelinus, in his work ‘Eclipses Lunares,’ says that the Moon “sometimes so far retains the light received from the Sun that you would doubt whether any part of it were eclipsed.” He cites the case of April 15, 1623. In the ‘ Chronological History’ aforesaid the year 1623 is mentioned among those in which the heavens were “on fiery flames.”
While volcanic eruptions may be connected with the dark type of lunar eclipse, it would seem that aurora was present when there was unusual effulgence [ed: brightness] on the Moon’s eclipsed surface.
The next time a bright type of eclipse is just possible will be on the morning of February 9, 1906, the Moon setting half “an hour after it is totally eclipsed at Greenwich ; but more would be seen in the western parts of Great Britain. At this time the slowly returning sun-spots, and coincidentally auroral displays, cannot be far from a maximum.
Yours faithfully, S.J. Johnson
Melplash Vicarage, Bridport, 1903, Aug. 11.
P.S.—The total lunar eclipse of 27 December, 1898, seems to have been of a somewhat bright character, far more so than usual, according to the remarks of some observers. The Moon did not come out of the clouds here until long past the total phase, but in the north of England the phenomenon seems to have been well observed. A coloured drawing of the Moon during totality, sent to me from Newcastle-on-Tyne, shows a bright scarlet hue; and let it be noted that in the ‘ Publications of West Hendon House Observatory, Sunderland,’ Mr. Backhouse puts down this 27th of December as one of the four nights in that year when there was an aurora, but marks it very faint. This might be somewhat enfeebled from the glare of distant lights in the neighbourhood. Rev. A. Killip remarks (vol. ix. no. 4) ‘ Journal B.A.A. ’ 1898-99: “11.30, whole Moon very distinct in every part.” Col. Markwick: “ The eclipse was a very bright one.” ”
Prediction
Prediction in astronomy is generally achieved through assessment of patterns. Astronomers use cycles to predict the recurrence of the eclipses.
See: Astronomical Prediction Based on Patterns - The Eclipses
Topics
- Electromagnetic Acceleration - EA Main Page
- Lunar Eclipse due to Electromagnetic Acceleration - The Lunar Eclipse occurs when the Moon moves beyond the Sun's light
- Moon Tilt Illusion - Illuminated portion of the Moon does not point in the expected direction
- Celestial Sphere - Lines become warped on a 'Celestial Sphere'
- High Altitude Horizon Dip - Horizon dip at high altitudes may suggest a bending of light
- Sunrise and Sunset - Sunrise and Sunset Main Page