Difference between revisions of "Moon Tilt Illusion Supplement"
Tom Bishop (talk | contribs) |
Tom Bishop (talk | contribs) |
||
| Line 48: | Line 48: | ||
[[File:Triangle_Calc_Result.png|800px]] | [[File:Triangle_Calc_Result.png|800px]] | ||
| − | We see a very thin Right Scalene Triangle. We see that the angle displacement of the Sun at Angle B is 0.147 degrees, as previously seen in the angular diameter calculator. We also see that Moon at Angle C is pointing downwards at 89.853 degrees; not exactly parallel to the baseline. | + | We see a very thin Right Scalene Triangle diagram. We see that the angle displacement of the Sun at Angle B is 0.147 degrees, as previously seen in the angular diameter calculator. We also see that Moon at Angle C is pointing downwards at 89.853 degrees; not exactly parallel to the baseline. |
[[File:Sun-parallel.png|350px]]<br> | [[File:Sun-parallel.png|350px]]<br> | ||
Revision as of 15:31, 28 June 2020
The Moon Tilt Illusion Supplement page addresses supplementary arguments related to the Moon Tilt Illusion.
Higher Sun Argument
As response to the Moon Tilt Illusion it is sometimes argued that the illuminated portion of the Moon is misaligned to the Sun since Sun's light is parallel and hitting the Earth-Moon system as a whole from the side, and so the Moon will see a higher Sun than an observer on the Earth. The Sun will appear from a different position in space to the Moon, causing the Moon's illuminated area to point to a position above the Sun that we see from Earth.
In contrast to this argument, the angles are not perfectly parallel under the Round Earth system. When assessing the parallax displacement between an observer on Earth and an observer on the Moon the Sun will be in essentially the same point in space.
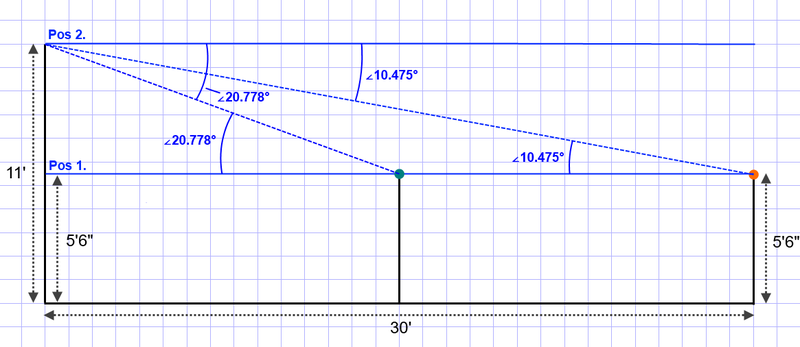
Angular Diameter Example
As an example, if your eye is at an altitude of 5 feet, 6 inches, and there is an object, say a Green Ball on a post 15 feet away from you at the same altitude, and an Orange Ball on a post 30 feet away from you, which are both also at altitudes of 5 feet, 6 inches, then the position of both the green and orange balls will be parallel on the horizontal. The path to those objects will be at your eye level.
Instead, lets say that you step on a boulder that is 5 foot, 6 inches in height. The new altitude of your eye is 11 feet in height. We know that the green and orange balls are on posts which are 5 ft 6 in below that 11 foot elevation where it would need to be to be parallel to the eye.
In order to find the position of the green and orange balls in degrees below eye level, we can use an angular diameter calculator to calculate the missing space above the green and orange ball, to determine how far below eye level those balls will be to the observer.
For the Green Ball, 5.5 feet at 15 feet produces an angular diameter of 20.778 degrees. For the Orange Ball, 5.5 feet at 30 feet produces an angular diameter of 10.475 degrees.
Diagram
We see that as a body moves further from you, it gets closer to your eye level, and displaces fewer degrees in space between two altitudes.
Adopting the above to the Earth and Moon in the RE system, we had from the previous diagram an observer seeing the Sun parallel on the horizontal at eye level, midway setting into the horizon. The Moon was over the observer. In order to calculate the displacement of the Sun in the between observers on Earth and the Moon we may use the angular diameter calculator with the distances involved in miles.
Input
g: 238900
r: 93000000
Output
a: 0.147 degrees
If the observer was able to move from the Earth to the Moon the Sun would be seen from essentially the same position in space. The diagram of the Sun appearing in two different places is misleading, as it does not show the entire scene and the angles are not exactly parallel to the Sun.
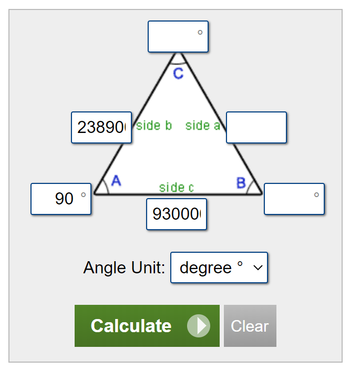
Triangle Calculator
Next, we look at a triangle calculator, which will compute the missing values in a triangle:
We put in the distances in miles to the RE Moon at Side b, the distance to the RE Sun at Side c, and 90 degrees at the observer at Angle A. This produces the following:
We see a very thin Right Scalene Triangle diagram. We see that the angle displacement of the Sun at Angle B is 0.147 degrees, as previously seen in the angular diameter calculator. We also see that Moon at Angle C is pointing downwards at 89.853 degrees; not exactly parallel to the baseline.
The Sun is not actually shining on the Earth and Moon in a parallel manner, but at slightly different angles.
Triangle Diagram
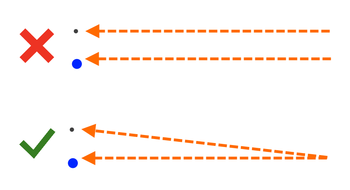
Now, consider the above thin Right Scalene Triangle diagram which was generated by the Triangle Calculator: If the object at Angle C was a Green Arrow pointing at the center of the Sun (Angle B), and if we could see both the Green Arrow and Sun at once in our field of vision (essentially the whole scene), would the the Green Arrow point at the Sun?
This should be true regardless of the shape of the triangle, and demonstrates the expectation that the illuminated portion of the Moon should point at the center of the Sun when viewed simultaneously. The Green Arrow should not point at a different spot in space.
Alignment with Sun Center
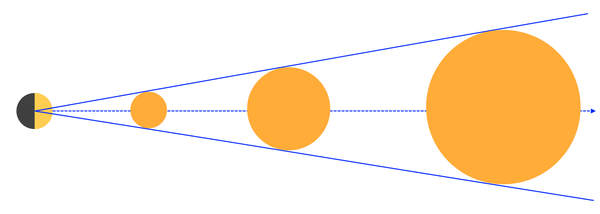
Finally, it is suggested that since the Sun is so large and the rays are essentially parallel to the relatively small Earth-Moon system at their distant location from the Sun, that the illuminated portion of the Moon is not necessarily pointing at the center of the Sun (restatement of premise).
Consider a situation where we have only have two bodies: The Moon and a Sun. The Sun starts as the size of the Moon (or smaller). The illuminated portion of the Moon will point at the center of that Sun. If the Sun continuously recedes in distance from the Moon and grows in size geometrically in a linear fashion, will the Moon ever not point at the center of the Sun?
Hence we see that, with only two bodies, the Moon will always point at the Sun's center, regardless of distance or size. There is no real reason for it to point anywhere else. From the position of the central hotspot upon the Moon's surface it will see the Sun directly 'overhead', and will be illuminated from directly 'overhead', regardless of how the Sun grows or recedes. The addition of an Earth somewhere around the Moon should not matter in regards to where the illuminated portion of the Moon points.